WBCE损失重写

2020.2.26 Updates

昨天写完今天发现 tf.nn.weighted_cross_entropy_with_logits……

WBCE

WBCE 即 weighted binary cross entropy，是 [1] 的公式 1，改版的 binary cross entropy。
$$L^{wbce}(y,z,w)=-\sum _{i=1}^c[w_i\cdot y_i\log z_i+(1-y_i)\log (1-z_i)]$$
其中，y 是真实 label 向量，z 是预测 label 向量，w 是权重向量， w i = # 0 { i } # 1 { i } w_i=\frac{\#0\{i\}}{\#1\{i\}} wi​=#1{i}#0{i}​， # 0 { i } \#0\{i\} #0{i} 是 training set 中不属于第 i 类的样本个数， # 1 { i } \#1\{i\} #1{i} 类似地表示属于的。
$w_i$ 是乘在中括号里面的。

Reformulation

当 z 是 sigmoid 的输出（如 [1] 的公式 4），记 $z=\sigma (x)$（$\sigma (\cdot )$ 表示 sigmoid 函数），参照 [2]，修改公式防溢出。

in scalar case

先按 y、z、w 都是标量的情况考虑：
$$\begin{array}{rl}{L}^{wbce}(y,z,w)& =-[w\cdot y\log z+(1-y)\log (1-z)]\\ & =-wy\log \sigma (x)-(1-y)\log [1-\sigma (x)]\\ & =wy\log (1+e^{-x})+(1-y)[x+\log (1+e^{-x})]\\ & =(wy+1-y)\log (1+e^{-x})+(1-y)x\end{array}$$
因为 $e^{-x}$ 在 $x<0$ 时很爆炸：

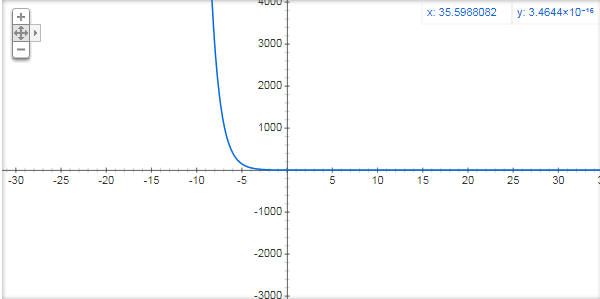
对 $x<0$ 的情况特殊处理，变形：
$$\begin{array}{rlr}{L}^{wbce}(y,z,w)& =(wy+1-y)\log (1+e^{-x})+(1-y)x& (1)\\ & =(wy+1-y)\log (1+e^{-x})+(wy+1-y)x-wyx& \\ & =(wy+1-y)[\log (1+e^{-x})+\log e^x]-wyx& \\ & =(wy+1-y)\log (1+e^x)-wyx& (2)\end{array}$$
(1) 式适用 $x\ge 0$ 的情况，(2) 适用在 $x<0$，于是：
L w b c e ( y , z , w ) = { ( w y + 1 − y ) log ⁡ ( 1 + e − x ) + ( 1 − y ) x , x ≥ 0 ( w y + 1 − y ) log ⁡ ( 1 + e x ) − w y x , x < 0 = ( w y + 1 − y ) log ⁡ ( 1 + e − ∣ x ∣ ) + max ⁡ { ( 1 − y ) x , 0 } − min ⁡ { w y x , 0 } \begin{aligned} L^{wbce}(y,z,w)&=\left\{\begin{array}{cc} (wy+1-y)\log(1+e^{-x})+(1-y)x, & x\ge0 \\ (wy+1-y)\log (1+e^x)-wyx, & x<0 \end{array}\right. \\ &=(wy+1-y)\log (1+e^{-|x|})+\max\{(1-y)x,0\}-\min\{wyx,0\} \end{aligned} Lwbce(y,z,w)​={(wy+1−y)log(1+e−x)+(1−y)x,(wy+1−y)log(1+ex)−wyx,​x≥0x<0​=(wy+1−y)log(1+e−∣x∣)+max{(1−y)x,0}−min{wyx,0}​
后面 max 和 min 两项是因为 y ∈ { 0 , 1 } y\in\{0,1\} y∈{0,1}、$w\ge 0$，所以 $(1-y)x$ 和 $wyx$ 的符号看 $x$。

in vector case

向量情况下类似，套上 ${\sum }_{i=1}^c$。

Implementation

tensorflow 版

# import tensorflow as tf

def WBCE_sigmoid(x, y, w):
    """WBCE with logit before sigmoid
    x: (n, c), prediction logit, z = sigmoid(x)
    y: (n, c), ground-truth label
    w: (c,), label weight
    """
    w = w[None, :]
    first = ((w - 1) * y + 1) * tf.math.log(1 + tf.math.exp(- tf.math.abs(x)))
    second = tf.math.maximum((1 - y) * x, 0)
    third = tf.math.minimum(w * y * x, 0)
    loss = tr.reduce_sum(first + second - third, axis=1)
    return tf.reduce_mean(loss)

References

1. Semi-Supervised Cross-Modal Retrieval with Label Prediction
2. tf.nn.sigmoid_cross_entropy_with_logits
3. Giving reasons on each line of a sequence of equations