2022-1-26 数据结构 全排列递归 三角形 哈夫曼树

全排列 递归

输出1-n（n<10）

#include<iostream>
#include<cmath>
using namespace std;
  
int p[10]= {0}; 
bool vis[10]= {0};
int n;
void dfs(int x) { 				// 从x到n的全排列
    if (x==n+1) {				//如果排序完n个数据后
        for(int i=1; i<=n; i++)	//输出一个排列
            cout<<p[i]<<" ";	
        cout<<endl;
        return ;
    }
  								//else 进行一组n个数据的排序
    for (int i=1; i<=n; i++) { // 从1开始排
        if (vis[i]==false  ) { // 标志符判断该数据是否已在排列中，每次for循环到新数字才执行
            p[x] = i;			// 将该数据加入排列中
            vis[i] = true;		// 改变该数字的标志符
            dfs(x+1);			// 递归加入下一位数字，直到n个数排完
            vis[i] = false;		// 从n向前标志符逐个变FALSE
        }
    }
}
  
int main() {
    while (cin>>n) { // 1-n 全排列
        dfs(1);
    }
    return 0;
}

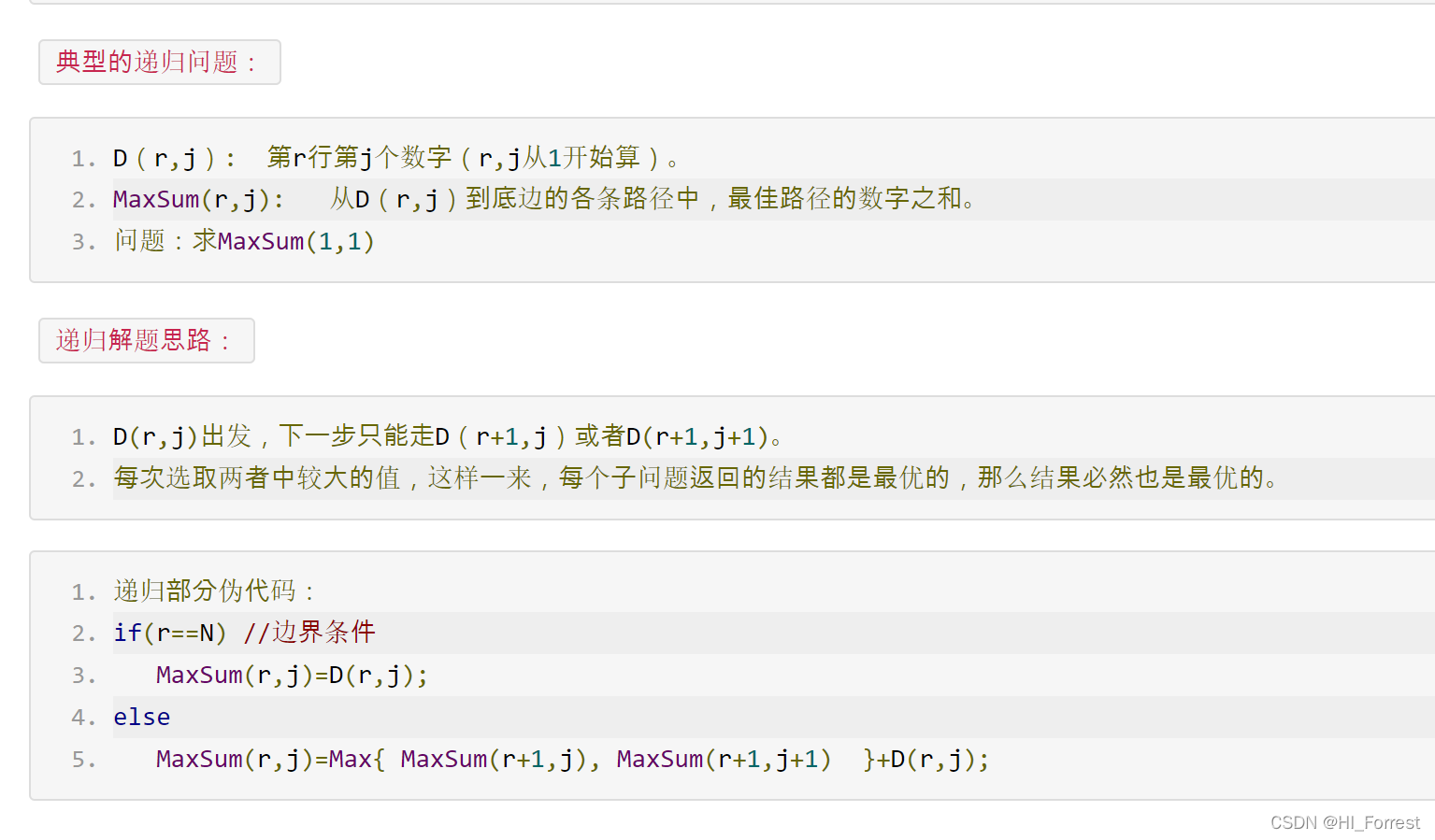
三角形

题解

#include<iostream>
#include<algorithm>
using namespace std;
#define MAX 101
int D[MAX][MAX];
int R[MAX][MAX];
int n, T;
int MaxSum(int i, int j) {
	if (i == n)	
	{		//到达最底行
		R[i][j] = D[i][j]; //直接存入结果三角形
		return D[i][j]; // 返回最下层单个数据
	}
	int x = MaxSum(i + 1, j); //向下一层的左
	int y = MaxSum(i + 1, j + 1);	//下一层的右
	std::cout << "node (" << i << ", " << j << ") is : " << max(x, y) + D[i][j] << endl;
	R[i][j] = max(x, y) + D[i][j]; //下一层左右的最大值加上本节点的值作为本节点向下的最大和
	return  max(x, y) + D[i][j];
}
int main() {
	int i, j;

	cin >> n;			//输入n行的数据
	for (i = 1; i <= n; i++)
	{							//
		for (j = 1; j <= i; j++)
		{
			cout << "input : D[" << i << "][" << j << "]" << endl;// 从上向下输入初始三角形
			cin >> D[i][j];
		}
	}
					
	cout << MaxSum(1, 1) << endl;

	for (i = 1; i <= n; i++)
	{							//
		for (j = 1; j <= i; j++)
		{
			//输出结果三角形
			cout << R[i][j] << "  ";
		}
		cout << endl;
	}


	return 0;
}

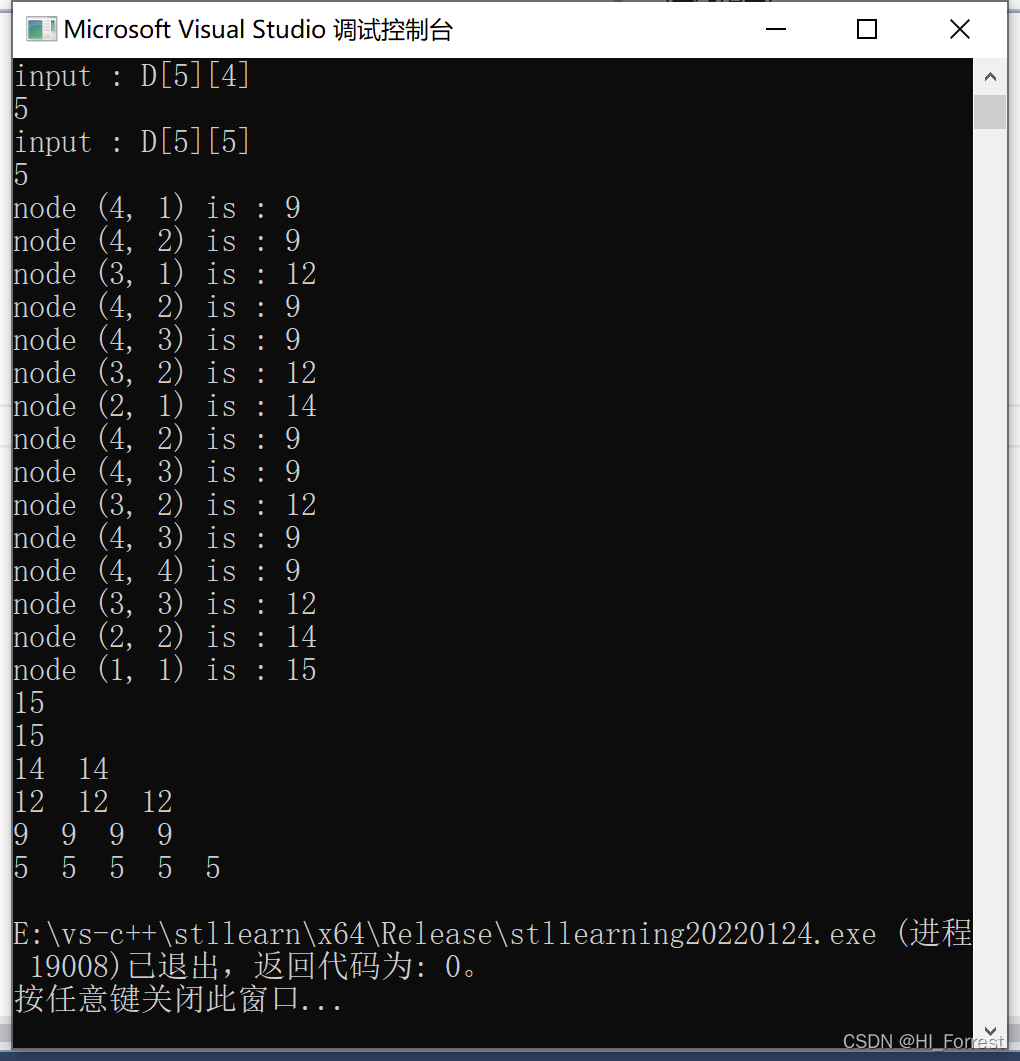
有重复计算

int MaxSum(int i,int j){
     if(maxSum[i][j]!=-1)return maxSum[i][j];//值不是-1，说明已经存下中间子问题的值
     if(i==n)
        return D[i][j];
     int x=MaxSum(i+1,j);
     int y=MaxSum(i+1,j+1);
     maxSum[i][j]=max(x,y)+D[i][j];
     return maxSum[i][j];
}
int main(){
   int i,j,k,t;
   while(cin>>T){
        while(T--){
           cin>>n;
           for(i=1;i<=n;i++)
            for(j=1;j<=i;j++){
                cin>>D[i][j];
                maxSum[i][j]=-1;//标记为-1
            }
           cout<<MaxSum(1,1)<<endl;
        }
   }
   return 0;
}

可以将计算过的节点最大值存起来，增加一个三角形标志符数组判断是否有结果，有则返回

从下到上的递推

#include<iostream>
#include<algorithm>
using namespace std;
int s[101][101],maxsum[101][101];
int main(){
    int n,c;
    while(cin>>c){
        while(c--)
        { 
            cin>>n;
            for(int i=1;i<=n;i++)
                for(int j=1;j<=i;j++){
                    cin>>s[i][j];
                    maxsum[i][j]=0;
                }
            for(int j=1;j<=n;j++)
                maxsum[n][j]=s[n][j];  
            for(int i=n-1;i>=1;i--){
                for(int j=1;j<=i;j++){
                    maxsum[i][j]=max(maxsum[i+1][j],maxsum[i+1][j+1])+s[i][j];
                }
            }
            cout<<maxsum[1][1]<<endl;    
        }     
    }    
    return 0;
}

哈夫曼树

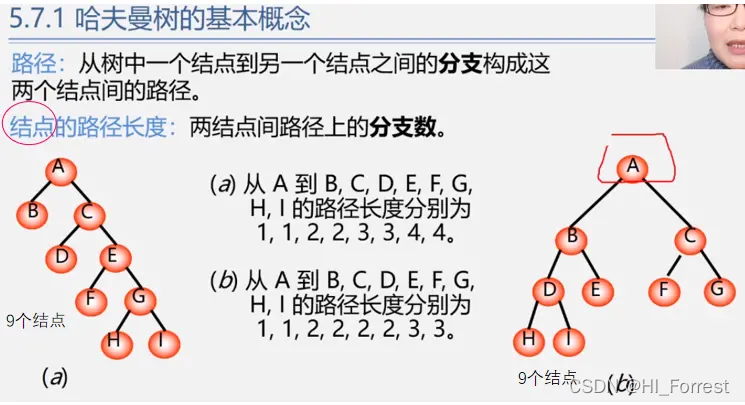
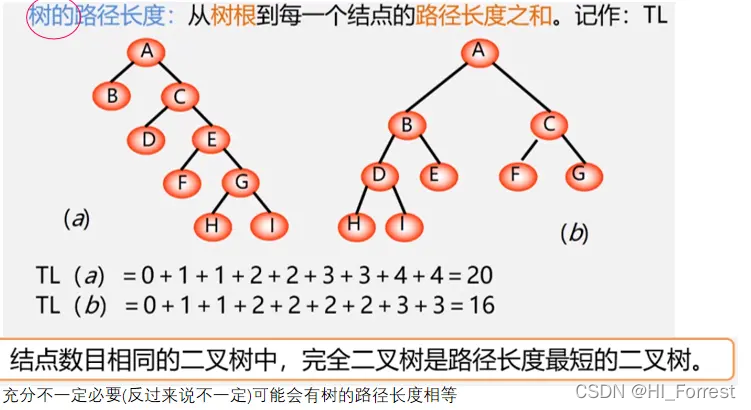
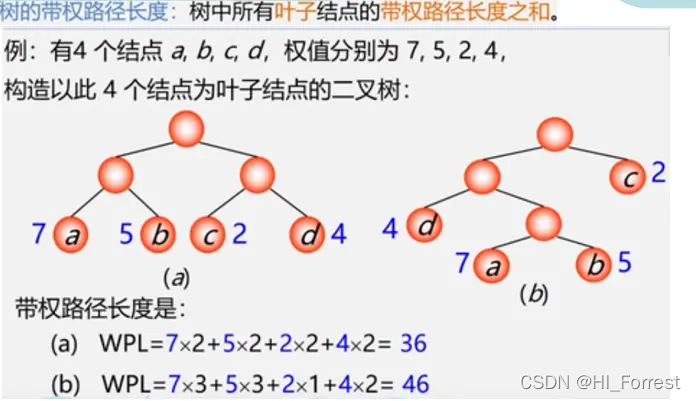
构造过程

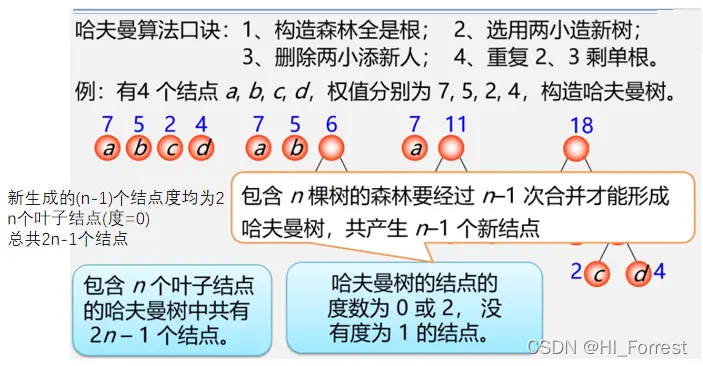
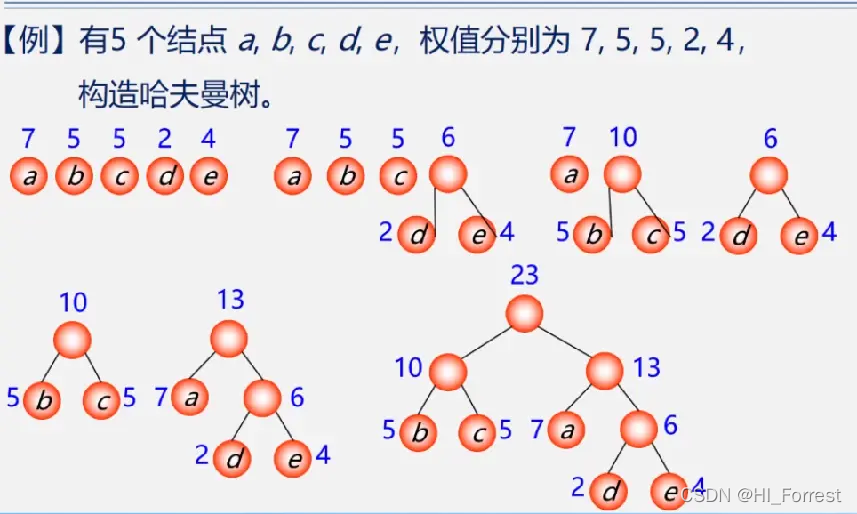
算法实现

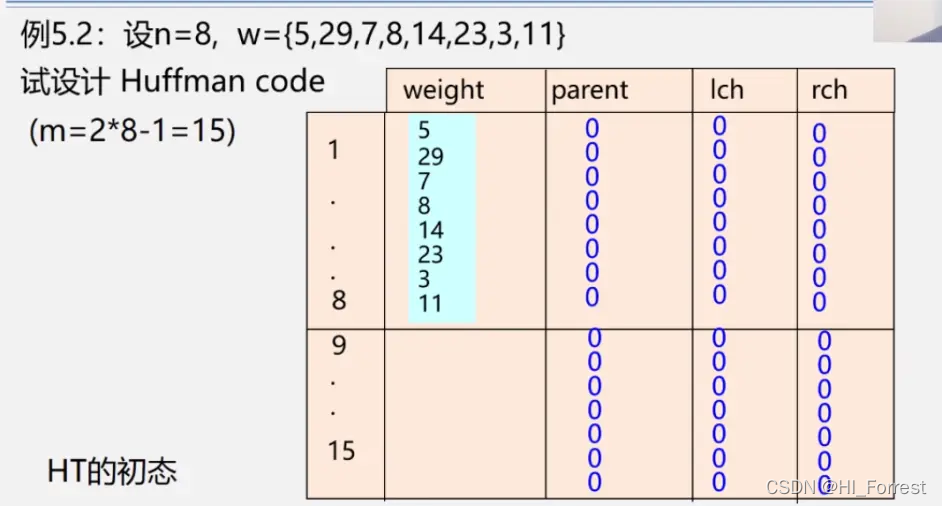
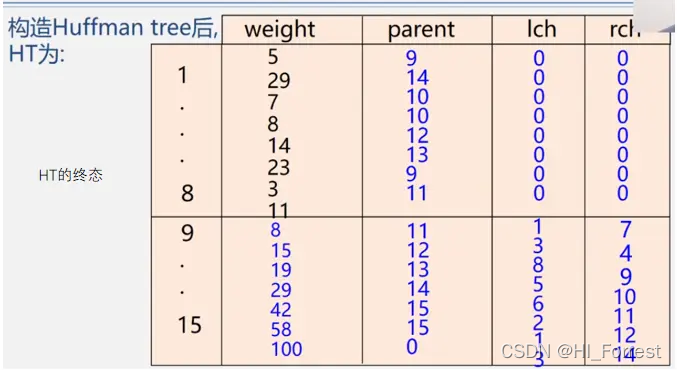
#include <iostream>


//哈夫曼树结点结构
typedef struct {
	int weight; //结点权重
	int parent, left, right;    //父结点、左孩子、右孩子在数组中的位置下标
} HTNode, *HuffmanTree;


//HT数组中存放的哈夫曼树，end表示HT数组中存放结点的最终位置，s1和s2传递的是HT数组中权重值最小的两个结点在数组中的位置
void Select(HuffmanTree HT, int end, int *s1, int *s2) {
	int min1, min2;
	//遍历数组初始下标为 1
	int i = 1;
	//找到还没构建树的结点
	while (HT[i].parent != 0 && i <= end) {
		i++;
	}
	min1 = HT[i].weight;
	*s1 = i;
	i++;
	while (HT[i].parent != 0 && i <= end) {
		i++;
	}
	//对找到的两个结点比较大小，min2为大的，min1为小的
	if (HT[i].weight < min1) {
		min2 = min1;
		*s2 = *s1;
		min1 = HT[i].weight;
		*s1 = i;
	}
	else {
		min2 = HT[i].weight;
		*s2 = i;
	}
	//两个结点和后续的所有未构建成树的结点做比较
	for (int j = i + 1; j <= end; j++) {
		//如果有父结点，直接跳过，进行下一个
		if (HT[j].parent != 0) {
			continue;
		}
		//如果比最小的还小，将min2=min1，min1赋值新的结点的下标
		if (HT[j].weight < min1) {
			min2 = min1;
			min1 = HT[j].weight;
			*s2 = *s1;
			*s1 = j;
		}
		//如果介于两者之间，min2赋值为新的结点的位置下标
		else if (HT[j].weight >= min1 && HT[j].weight < min2) {
			min2 = HT[j].weight;
			*s2 = j;
		}
	}
}

//HT为地址传递的存储哈夫曼树的数组，w为存储结点权重值的数组，n为结点个数
void CreateHuffmanTree(HuffmanTree *HT, int *w, int n) {
	if (n <= 1)
		return; // 如果只有一个编码就相当于0
	int m = 2 * n - 1; // 哈夫曼树总节点数，n就是叶子结点
	*HT = (HuffmanTree)malloc((m + 1) * sizeof(HTNode)); // 0号位置不用
	HuffmanTree p = *HT;
	// 初始化哈夫曼树中的所有结点
	for (int i = 1; i <= n; i++) {
		(p + i)->weight = *(w + i - 1);
		(p + i)->parent = 0;
		(p + i)->left = 0;
		(p + i)->right = 0;
	}
	//从树组的下标 n+1 开始初始化哈夫曼树中除叶子结点外的结点
	for (int i = n + 1; i <= m; i++) {
		(p + i)->weight = 0;
		(p + i)->parent = 0;
		(p + i)->left = 0;
		(p + i)->right = 0;
	}
	//构建哈夫曼树
	for (int i = n + 1; i <= m; i++) {
		int s1, s2;
		Select(*HT, i - 1, &s1, &s2);    //查找内容，需要用到查找算法
		(*HT)[s1].parent = (*HT)[s2].parent = i;
		(*HT)[i].left = s1;
		(*HT)[i].right = s2;
		(*HT)[i].weight = (*HT)[s1].weight + (*HT)[s2].weight;
	}

	for (int i = 1; i <= m; i++)
	{
		std::cout << "node " << i << " : ";
		std::cout << (p + i)->weight << ", " << (p+i)->parent << ", " << (p + i)->left << ", " << (p+i)->right  << std::endl;
	}

}

int main()
{
	int weight[6] = { 1,2,3,4,5,6 };
	int num = 6;
	HuffmanTree tree;
	CreateHuffmanTree(&tree, weight, num);
}