实验1:MLPClassifier构建神经网络完成手写数字分类
一、实验目的
1. 掌握使用sklearn机器学习库构建神经网络模型的方法
2. 理解多层感知器(MLP)在分类任务中的应用
3. 学习评估和优化神经网络模型性能的方法
二、实验步骤
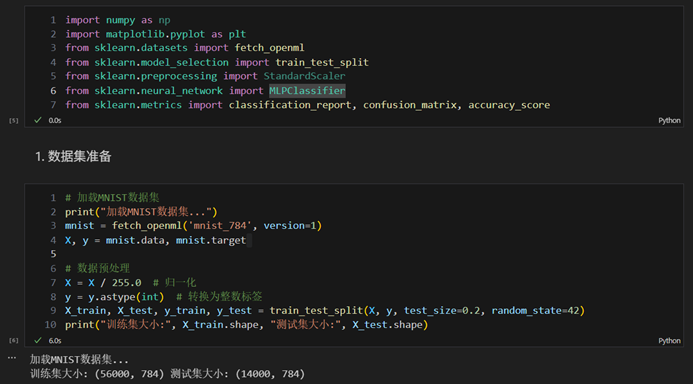
- 数据集准备
- 加载MNIST数据集
- 数据预处理(归一化、划分训练集和测试集)
- 模型构建
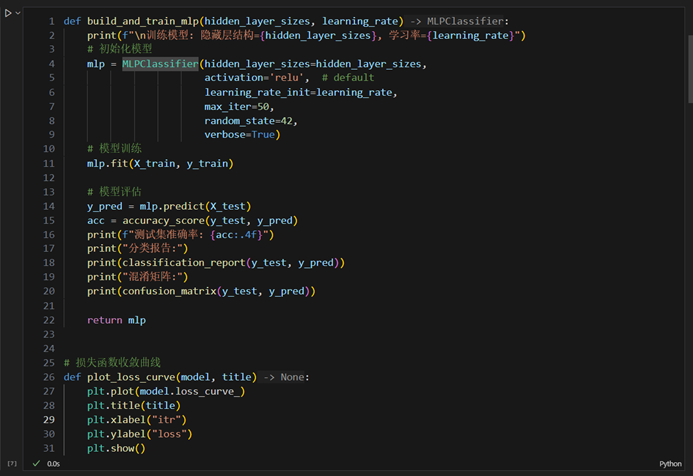
- 设计网络结构(隐藏层大小、层数等)
- 设置模型参数(学习率、激活函数、优化器等)
- 模型训练与测试
- 训练过程记录
- 测试集评估
三、实验结果
- 代码一份
- 训练过程分析
- 损失函数收敛曲线
- 模型性能评估
- 在测试集上的准确率
- 混淆矩阵
- 分类报告(准确率、召回率、F1分数)
四、实验讨论与分析
- 学习率影响分析
实验要求:尝试不同的学习率(0.1、0.01、0.001)对模型性能表现,并记录实验结果。

1.1训练模型: 隐藏层结构=(100,), 学习率=0.1
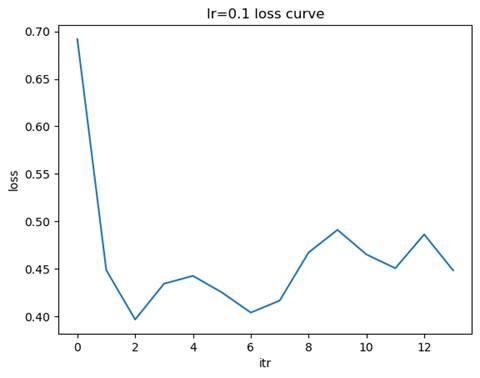
测试集准确率: 0.9054
混淆矩阵:
[[1272 0 1 0 1 0 8 2 57 2]
[ 0 1547 6 8 1 3 1 4 29 1]
[ 2 4 1271 4 7 0 8 4 77 3]
[ 4 0 55 1237 0 25 0 12 90 10]
[ 1 0 1 1 1138 4 5 5 79 61]
[ 3 4 1 48 9 1019 14 1 166 8]
[ 6 1 7 0 4 16 1304 0 58 0]
[ 7 3 51 1 2 0 0 1353 45 41]
[ 3 8 24 12 5 3 14 2 1282 4]
[ 4 3 0 13 19 0 1 26 102 1252]]
分类报告:
precision recall f1-score support
0 0.98 0.95 0.96 1343
1 0.99 0.97 0.98 1600
2 0.90 0.92 0.91 1380
3 0.93 0.86 0.90 1433
4 0.96 0.88 0.92 1295
5 0.95 0.80 0.87 1273
6 0.96 0.93 0.95 1396
7 0.96 0.90 0.93 1503
8 0.65 0.94 0.77 1357
9 0.91 0.88 0.89 1420
accuracy 0.91 14000
macro avg 0.92 0.90 0.91 14000
weighted avg 0.92 0.91 0.91 14000
-
- 训练模型: 隐藏层结构=(100,), 学习率=0.01
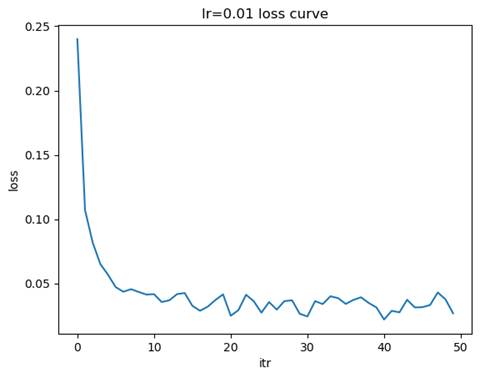
测试集准确率: 0.9750
混淆矩阵:
[[1325 0 4 0 1 1 3 1 7 1]
[ 0 1582 2 2 2 0 0 4 8 0]
[ 0 3 1352 0 1 2 3 2 16 1]
[ 2 2 19 1374 1 10 0 2 16 7]
[ 3 0 3 0 1252 0 4 4 8 21]
[ 2 3 1 11 1 1226 7 1 17 4]
[ 6 0 1 0 4 1 1370 0 14 0]
[ 1 3 12 2 5 1 0 1460 8 11]
[ 0 2 7 1 3 2 4 3 1332 3]
[ 3 3 2 3 9 2 0 7 14 1377]]
分类报告:
precision recall f1-score support
0 0.99 0.99 0.99 1343
1 0.99 0.99 0.99 1600
2 0.96 0.98 0.97 1380
3 0.99 0.96 0.97 1433
4 0.98 0.97 0.97 1295
5 0.98 0.96 0.97 1273
6 0.98 0.98 0.98 1396
7 0.98 0.97 0.98 1503
8 0.93 0.98 0.95 1357
9 0.97 0.97 0.97 1420
accuracy 0.97 14000
macro avg 0.98 0.97 0.97 14000
weighted avg 0.98 0.97 0.98 14000
-
- 训练模型: 隐藏层结构=(100,), 学习率=0.001
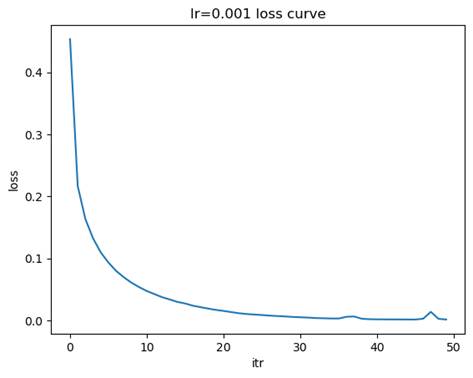
测试集准确率: 0.9751
混淆矩阵:
[[1324 1 2 0 0 0 5 3 5 3]
[ 0 1586 3 2 1 0 1 5 1 1]
[ 3 5 1331 4 2 3 6 7 16 3]
[ 0 1 16 1380 2 11 2 6 5 10]
[ 0 1 3 0 1265 0 2 2 3 19]
[ 1 2 0 16 3 1233 8 1 8 1]
[ 0 0 1 0 3 4 1385 1 2 0]
[ 1 3 13 2 3 2 0 1464 0 15]
[ 6 7 7 8 5 3 7 3 1303 8]
[ 5 4 1 5 12 4 0 3 6 1380]]
分类报告:
precision recall f1-score support
0 0.99 0.99 0.99 1343
1 0.99 0.99 0.99 1600
2 0.97 0.96 0.97 1380
3 0.97 0.96 0.97 1433
4 0.98 0.98 0.98 1295
5 0.98 0.97 0.97 1273
6 0.98 0.99 0.99 1396
7 0.98 0.97 0.98 1503
8 0.97 0.96 0.96 1357
9 0.96 0.97 0.97 1420
accuracy 0.98 14000
macro avg 0.97 0.97 0.97 14000
weighted avg 0.98 0.98 0.98 14000
问题讨论:
- 比较不同学习率下损失函数的收敛速度
学习率较大(如 0.1):损失函数的下降速度较快,但可能会出现震荡,甚至无法收敛。学习率适中(如 0.01):损失函数下降平稳,收敛速度适中,通常是较优的选择。学习率较小(如 0.001):损失函数下降非常缓慢但最平稳,可能需要更多的迭代次数才能达到收敛。
- 分析学习率过大和过小分别会导致什么问题
学习率过大模型可能无法收敛,损失函数在较高值附近震荡。
原因:每次梯度更新的步长过大,可能越过最优点。
现象:训练过程中的损失值波动较大,测试集准确率较低。
学习率过小模型收敛速度过慢,训练时间显著增加。
原因:每次梯度更新的步长过小,导致优化过程效率低下。
现象:损失函数下降缓慢,可能在有限的迭代次数内未达到最优点。
- 结合实验结果,讨论如何选择合适的学习率
学习率应在保证收敛稳定性的同时,尽可能加快收敛速度。通过实验观察,选择一个既能快速收敛又能稳定达到较低损失值的学习率。如果 0.1 学习率导致震荡,而 0.001 学习率收敛过慢,则 0.01 是一个较好的折中选择。可以结合损失函数曲线和测试集准确率,进一步验证选择的学习率是否合适。
在实际任务中,可以使用学习率调度器(如 learning_rate='adaptive')动态调整学习率。初始学习率可以从 0.01 开始,逐步尝试调整,找到适合当前任务的最佳值。
- 网络结构影响分析:
2.1隐藏层节点数量影响分析
实验要求:使用单隐藏层,尝试不同的节点数量(20、50、100、200),并记录实验结果。

2.1.1 训练模型: 隐藏层结构=(20,), 学习率=0.01
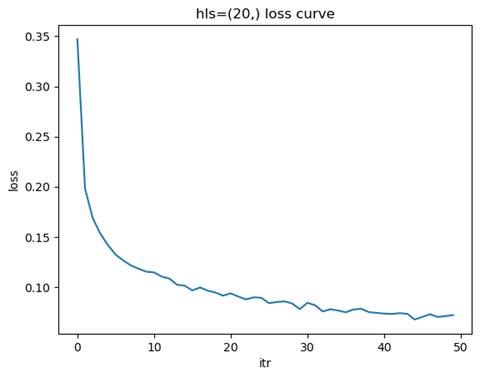
测试集准确率: 0.9461
混淆矩阵:
[[1307 0 3 0 1 7 10 6 8 1]
[ 1 1567 7 5 1 0 3 4 10 2]
[ 9 13 1285 13 13 3 8 11 23 2]
[ 1 15 29 1320 2 28 4 11 16 7]
[ 4 0 3 5 1219 5 7 7 6 39]
[ 6 9 0 26 2 1196 15 2 15 2]
[ 9 6 8 0 12 15 1341 0 3 2]
[ 11 6 15 5 3 7 0 1414 4 38]
[ 6 17 10 14 5 22 6 5 1257 15]
[ 7 7 1 7 16 13 0 11 19 1339]]
分类报告:
precision recall f1-score support
0 0.96 0.97 0.97 1343
1 0.96 0.98 0.97 1600
2 0.94 0.93 0.94 1380
3 0.95 0.92 0.93 1433
4 0.96 0.94 0.95 1295
5 0.92 0.94 0.93 1273
6 0.96 0.96 0.96 1396
7 0.96 0.94 0.95 1503
8 0.92 0.93 0.92 1357
9 0.93 0.94 0.93 1420
accuracy 0.95 14000
macro avg 0.95 0.95 0.95 14000
weighted avg 0.95 0.95 0.95 14000
2.1.2 训练模型: 隐藏层结构=(50,), 学习率=0.01
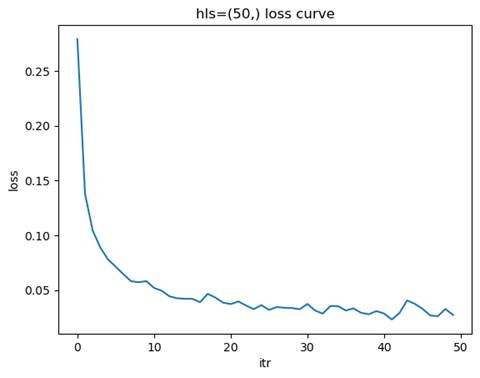
测试集准确率: 0.9651
混淆矩阵:
[[1314 0 3 0 4 3 3 3 8 5]
[ 0 1588 5 3 1 0 1 2 0 0]
[ 9 11 1323 10 5 0 2 8 7 5]
[ 1 5 18 1368 1 20 1 6 4 9]
[ 3 1 5 2 1239 1 6 2 0 36]
[ 7 4 1 19 4 1204 7 0 17 10]
[ 5 0 0 0 6 8 1371 0 6 0]
[ 3 4 17 4 4 0 1 1446 1 23]
[ 5 8 11 8 4 11 3 13 1284 10]
[ 4 6 1 8 8 2 0 11 6 1374]]
分类报告:
precision recall f1-score support
0 0.97 0.98 0.98 1343
1 0.98 0.99 0.98 1600
2 0.96 0.96 0.96 1380
3 0.96 0.95 0.96 1433
4 0.97 0.96 0.96 1295
5 0.96 0.95 0.95 1273
6 0.98 0.98 0.98 1396
7 0.97 0.96 0.97 1503
8 0.96 0.95 0.95 1357
9 0.93 0.97 0.95 1420
accuracy 0.97 14000
macro avg 0.97 0.96 0.96 14000
weighted avg 0.97 0.97 0.97 14000
2.1.3 训练模型: 隐藏层结构=(100,), 学习率=0.01

测试集准确率: 0.9750
分类报告:
precision recall f1-score support
0 0.99 0.99 0.99 1343
1 0.99 0.99 0.99 1600
2 0.96 0.98 0.97 1380
3 0.99 0.96 0.97 1433
4 0.98 0.97 0.97 1295
5 0.98 0.96 0.97 1273
6 0.98 0.98 0.98 1396
7 0.98 0.97 0.98 1503
8 0.93 0.98 0.95 1357
9 0.97 0.97 0.97 1420
accuracy 0.97 14000
macro avg 0.98 0.97 0.97 14000
weighted avg 0.98 0.97 0.98 14000
混淆矩阵:
[[1325 0 4 0 1 1 3 1 7 1]
[ 0 1582 2 2 2 0 0 4 8 0]
[ 0 3 1352 0 1 2 3 2 16 1]
[ 2 2 19 1374 1 10 0 2 16 7]
[ 3 0 3 0 1252 0 4 4 8 21]
[ 2 3 1 11 1 1226 7 1 17 4]
[ 6 0 1 0 4 1 1370 0 14 0]
[ 1 3 12 2 5 1 0 1460 8 11]
[ 0 2 7 1 3 2 4 3 1332 3]
[ 3 3 2 3 9 2 0 7 14 1377]]
2.1.4 训练模型: 隐藏层结构=(200,), 学习率=0.01
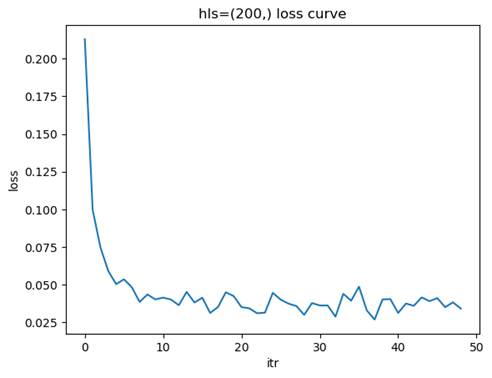
测试集准确率: 0.9758
分类报告:
precision recall f1-score support
0 0.98 0.99 0.98 1343
1 0.99 0.99 0.99 1600
2 0.97 0.98 0.97 1380
3 0.98 0.97 0.97 1433
4 0.98 0.97 0.98 1295
5 0.97 0.97 0.97 1273
6 0.98 0.98 0.98 1396
7 0.98 0.97 0.98 1503
8 0.96 0.97 0.96 1357
9 0.96 0.97 0.97 1420
accuracy 0.98 14000
macro avg 0.98 0.98 0.98 14000
weighted avg 0.98 0.98 0.98 14000
混淆矩阵:
[[1323 0 6 0 1 3 3 1 5 1]
[ 0 1582 2 5 1 0 0 3 6 1]
[ 2 4 1346 5 2 1 2 4 13 1]
[ 2 2 15 1387 0 12 0 2 8 5]
[ 2 2 0 0 1262 0 6 3 1 19]
[ 1 0 1 5 1 1241 10 0 12 2]
[ 3 1 0 0 5 7 1370 1 9 0]
[ 1 2 17 2 2 2 0 1453 3 21]
[ 7 3 5 5 4 2 3 3 1317 8]
[ 4 3 0 6 10 7 0 6 4 1380]]
问题讨论:节点数量如何影响模型的学习能力?
节点数量对模型的学习能力有着显著影响。节点数量较少时,模型的表达能力有限,无法捕捉数据中的复杂特征,容易导致欠拟合现象。这种情况下,训练集和测试集的准确率都较低,损失函数下降缓慢且可能在较高值附近收敛。随着节点数量的增加,模型的表达能力逐渐增强,能够更好地拟合数据中的特征,测试集准确率也随之提高,损失函数下降平稳且收敛速度适中。然而,当节点数量过多时,模型的复杂度过高,可能会导致过拟合问题,表现为训练集准确率很高,但测试集准确率下降,泛化能力变差,同时训练时间和计算资源的需求也会显著增加。
因此,选择合适的节点数量需要综合考虑数据的复杂度和规模。如果数据特征较为复杂或数据量较大,可以适当增加节点数量以增强模型的表达能力;而对于简单数据或数据量较少的情况,应减少节点数量以避免过拟合。通过实验验证不同节点数量下的模型性能,观察测试集准确率和损失函数的变化,可以帮助找到欠拟合与过拟合之间的平衡点,从而选择最优的节点数量。
2.2层结构影响分析:
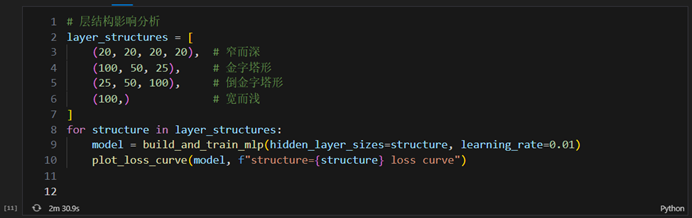
实验要求:保持总参数量相近(约1万个参数),尝试不同的层结构并记录实验结果。
- 窄而深:(20,20,20,20)
- 金字塔形:(100,50,25)
- 倒金字塔形:(25,50,100)
- 宽而浅:(100,)

-
-
- 训练模型: 隐藏层结构=(20, 20, 20, 20), 学习率=0.01
-
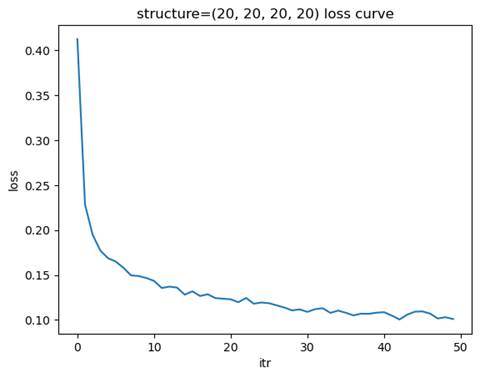
测试集准确率: 0.9468
混淆矩阵:
[[1305 0 10 0 1 2 6 1 12 6]
[ 0 1561 14 2 4 1 1 6 10 1]
[ 5 1 1323 9 10 2 8 11 9 2]
[ 1 1 21 1319 1 24 3 21 32 10]
[ 7 1 11 0 1251 0 3 4 3 15]
[ 3 3 8 30 9 1178 5 4 24 9]
[ 11 2 12 0 6 15 1339 1 10 0]
[ 4 2 21 2 10 1 0 1447 1 15]
[ 7 10 16 11 7 9 3 6 1278 10]
[ 5 3 1 9 91 2 0 35 20 1254]]
分类报告:
precision recall f1-score support
0 0.97 0.97 0.97 1343
1 0.99 0.98 0.98 1600
2 0.92 0.96 0.94 1380
3 0.95 0.92 0.94 1433
4 0.90 0.97 0.93 1295
5 0.95 0.93 0.94 1273
6 0.98 0.96 0.97 1396
7 0.94 0.96 0.95 1503
8 0.91 0.94 0.93 1357
9 0.95 0.88 0.91 1420
accuracy 0.95 14000
macro avg 0.95 0.95 0.95 14000
weighted avg 0.95 0.95 0.95 14000
-
-
- 训练模型: 隐藏层结构=(100, 50, 25), 学习率=0.01
-
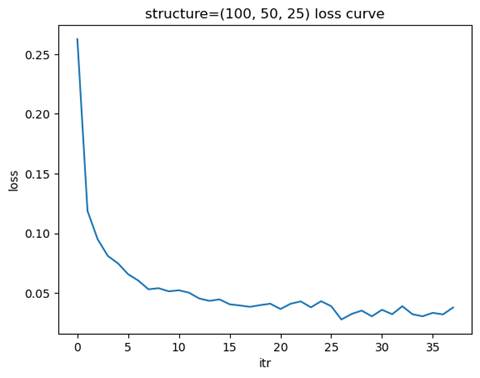
测试集准确率: 0.9727
混淆矩阵:
[[1329 1 2 0 1 0 1 0 8 1]
[ 0 1584 3 2 2 0 1 6 2 0]
[ 5 6 1341 6 5 0 0 6 8 3]
[ 1 1 11 1378 0 12 0 10 19 1]
[ 2 0 3 1 1253 1 3 2 10 20]
[ 2 1 0 10 1 1231 12 1 13 2]
[ 2 1 3 0 3 8 1373 0 5 1]
[ 2 5 11 1 0 3 0 1472 4 5]
[ 4 9 6 4 5 7 3 5 1311 3]
[ 6 3 0 6 12 5 1 18 23 1346]]
分类报告:
precision recall f1-score support
0 0.98 0.99 0.99 1343
1 0.98 0.99 0.99 1600
2 0.97 0.97 0.97 1380
3 0.98 0.96 0.97 1433
4 0.98 0.97 0.97 1295
5 0.97 0.97 0.97 1273
6 0.98 0.98 0.98 1396
7 0.97 0.98 0.97 1503
8 0.93 0.97 0.95 1357
9 0.97 0.95 0.96 1420
accuracy 0.97 14000
macro avg 0.97 0.97 0.97 14000
weighted avg 0.97 0.97 0.97 14000
-
-
- 训练模型: 隐藏层结构=(25, 50, 100), 学习率=0.01
-
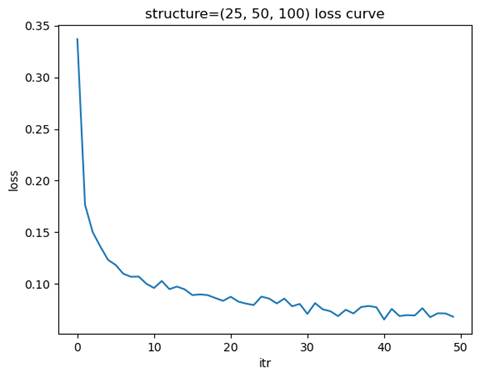
测试集准确率: 0.9590
混淆矩阵:
[[1312 1 3 1 2 7 9 0 7 1]
[ 0 1580 1 5 2 0 1 3 7 1]
[ 2 4 1330 6 4 5 3 9 15 2]
[ 0 1 15 1376 1 9 2 6 13 10]
[ 2 0 5 0 1242 1 13 4 3 25]
[ 4 2 6 40 2 1182 19 0 12 6]
[ 8 1 2 0 9 9 1362 0 5 0]
[ 4 4 19 4 12 4 0 1431 7 18]
[ 6 7 16 21 5 12 8 4 1267 11]
[ 4 5 1 5 39 4 1 10 7 1344]]
分类报告:
precision recall f1-score support
0 0.98 0.98 0.98 1343
1 0.98 0.99 0.99 1600
2 0.95 0.96 0.96 1380
3 0.94 0.96 0.95 1433
4 0.94 0.96 0.95 1295
5 0.96 0.93 0.94 1273
6 0.96 0.98 0.97 1396
7 0.98 0.95 0.96 1503
8 0.94 0.93 0.94 1357
9 0.95 0.95 0.95 1420
accuracy 0.96 14000
macro avg 0.96 0.96 0.96 14000
weighted avg 0.96 0.96 0.96 14000
-
-
- 训练模型: 隐藏层结构=(100,), 学习率=0.01
-
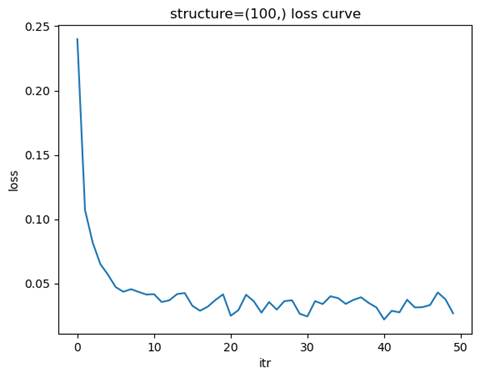
测试集准确率: 0.9750
混淆矩阵:
[[1325 0 4 0 1 1 3 1 7 1]
[ 0 1582 2 2 2 0 0 4 8 0]
[ 0 3 1352 0 1 2 3 2 16 1]
[ 2 2 19 1374 1 10 0 2 16 7]
[ 3 0 3 0 1252 0 4 4 8 21]
[ 2 3 1 11 1 1226 7 1 17 4]
[ 6 0 1 0 4 1 1370 0 14 0]
[ 1 3 12 2 5 1 0 1460 8 11]
[ 0 2 7 1 3 2 4 3 1332 3]
[ 3 3 2 3 9 2 0 7 14 1377]]
分类报告:
precision recall f1-score support
0 0.99 0.99 0.99 1343
1 0.99 0.99 0.99 1600
2 0.96 0.98 0.97 1380
3 0.99 0.96 0.97 1433
4 0.98 0.97 0.97 1295
5 0.98 0.96 0.97 1273
6 0.98 0.98 0.98 1396
7 0.98 0.97 0.98 1503
8 0.93 0.98 0.95 1357
9 0.97 0.97 0.97 1420
accuracy 0.97 14000
macro avg 0.98 0.97 0.97 14000
weighted avg 0.98 0.97 0.98 14000
问题讨论:哪种网络结构最合适?在保持参数量相近的情况下,层数和宽度如何权衡?
选择金字塔型结构最合适,其在较少的迭代次数下达到了近似最优的测试集准确率。
在保持参数量相近的情况下,网络结构的层数和宽度需要根据任务的复杂性和数据特征进行权衡。不同的网络结构(如窄而深、宽而浅、金字塔形、倒金字塔形)各有优劣,适合不同的应用场景。
窄而深的网络结构(如 (20, 20, 20, 20))通过增加层数来捕捉数据的复杂特征,适合处理具有高度非线性关系的数据。这种结构能够逐层提取特征,但训练时间较长,且可能面临梯度消失或梯度爆炸的问题,需要更好的优化器和正则化方法来稳定训练。
宽而浅的网络结构(如 (100,))通过增加每层的节点数量来增强模型的表达能力,适合处理简单或中等复杂度的数据。这种结构训练速度较快,但可能无法充分提取深层次特征,容易在复杂任务中表现不足。
金字塔形结构(如 (100, 50, 25))通过逐层减少节点数量,能够在前层提取更多的全局特征,后层逐步聚焦于更具体的特征。这种结构在许多任务中表现良好,兼顾了特征提取能力和计算效率。
倒金字塔形结构(如 (25, 50, 100))通过逐层增加节点数量,适合需要逐步扩展特征空间的任务,但在大多数情况下,这种结构的表现不如金字塔形或窄而深的结构。
在权衡层数和宽度时,需要考虑以下因素:数据的复杂性、训练数据量和计算资源。如果数据复杂且训练数据量充足,可以选择窄而深或金字塔形结构以增强特征提取能力;如果数据简单或计算资源有限,可以选择宽而浅的结构以提高训练效率。最终,最合适的网络结构通常需要通过实验验证,结合测试集的准确率、损失函数的收敛情况以及模型的泛化能力来确定。
实验2:MLPRegressor构建神经网络预测学生成绩
一、实验目的
掌握神经网络在回归任务中的应用方法
熟悉基本的数据预处理方法
二、实验结果
- 代码一份
- 训练过程分析
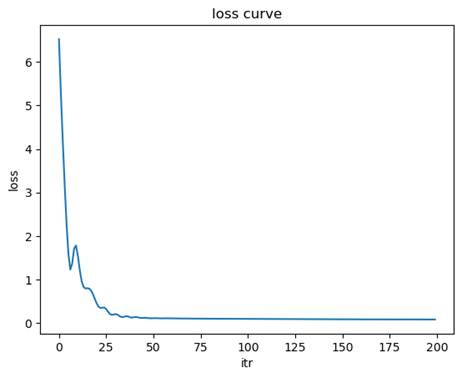
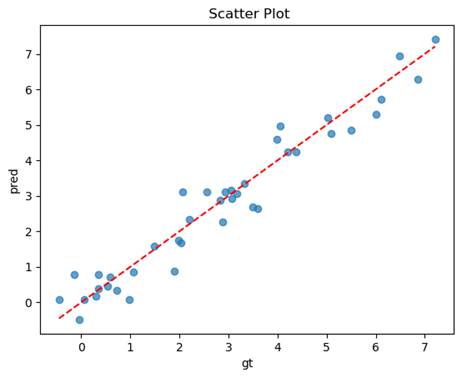
损失函数收敛曲线
- 模型性能评估
均方误差(MSE)
决定系数(R2)
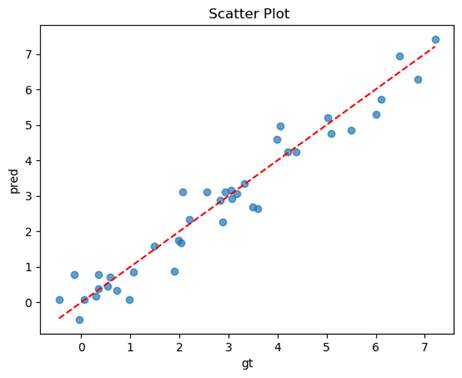
预测值与真实值的散点图
三、实验讨论与分析
- 不同特征对模型预测的影响分析
实验要求:分析不同特征对预测结果的影响
原始 MSE: 0.2219
特征 Feature 1 置零后 MSE: 3.1137,变化: 2.8919
特征 Feature 2 置零后 MSE: 1.7032,变化: 1.4813
特征 Feature 3 置零后 MSE: 0.5121,变化: 0.2902
特征 Feature 4 置零后 MSE: 0.3769,变化: 0.1550
特征 Feature 5 置零后 MSE: 4.0887,变化: 3.8669
问题讨论:哪类特征对预测学生成绩最重要?为什么?
当某个特征被置零后,MSE 的变化量越大,说明该特征对模型预测的贡献越大。如果置零某个特征后,MSE 几乎没有变化,说明该特征对模型预测的影响较小,可能是一个冗余特征。
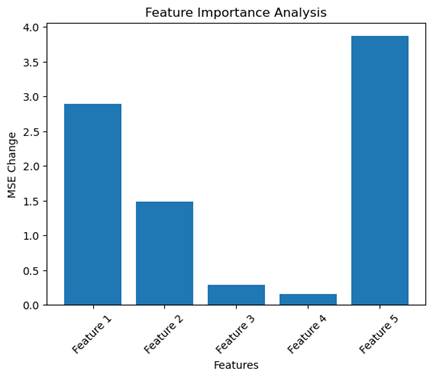
特征 Feature 5 的 MSE 变化最大(3.8669),说明它对模型预测最重要。特征 Feature 1 的 MSE 变化次大(2.8919),说明它也是一个关键特征。特征 Feature 2 的 MSE 变化为 1.4813,说明它对预测有一定影响,但不如 Feature 1 和 Feature 5。特征 Feature 3 和 Feature 4 的 MSE 变化较小(分别为 0.2902 和 0.1550),说明它们对模型预测的贡献较低。
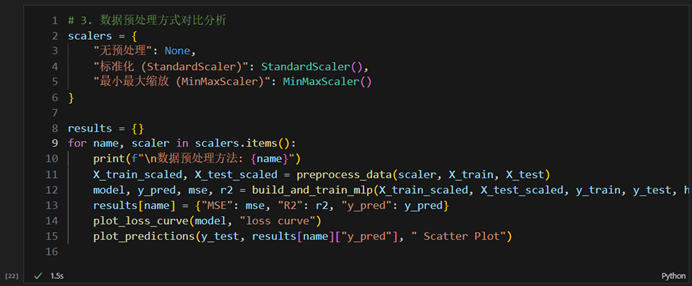
- 数据预处理方式对比分析
实验要求; 对比不同预处理方法对模型性能的影响,并记录实验结果
- 无预处理(原始数据)
- 标准化(StandardScaler):减均值除方差
- 最小最大缩放(MinMaxScaler):缩放到[0,1]区间
-
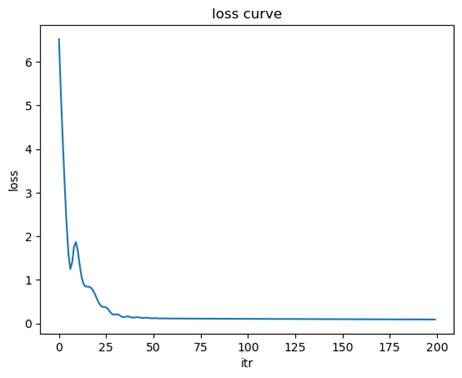
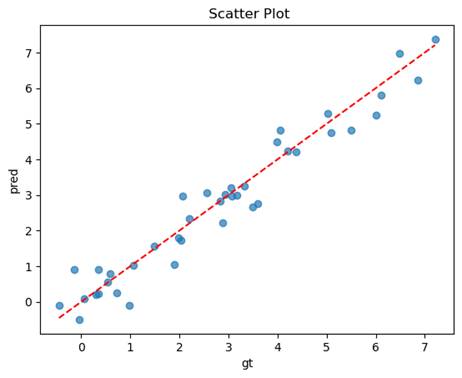
- 无预处理
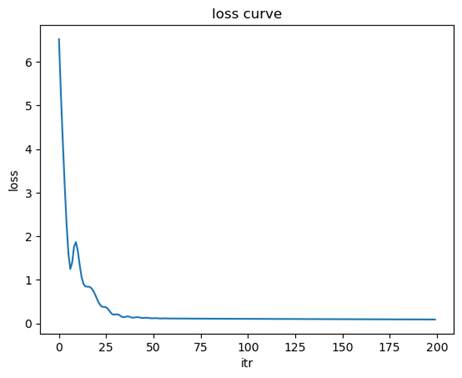
均方误差(MSE): 0.2470
决定系数(R2): 0.9438
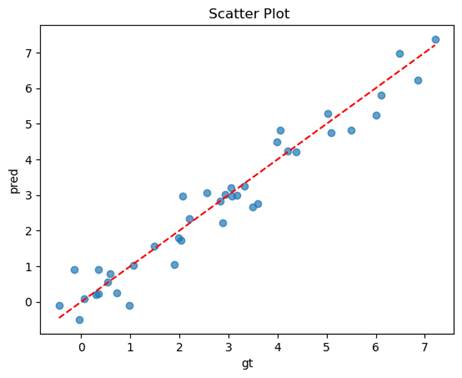
-
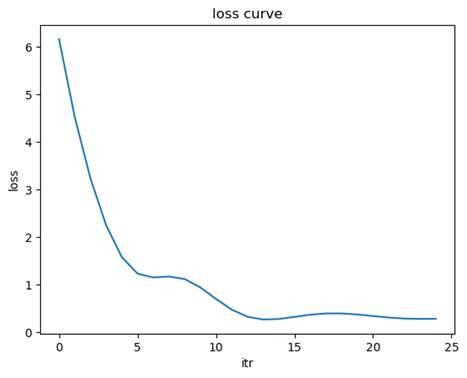
- 标准化
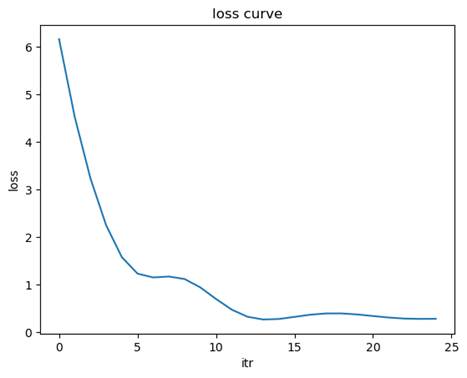
均方误差(MSE): 0.5784
决定系数(R2): 0.8685
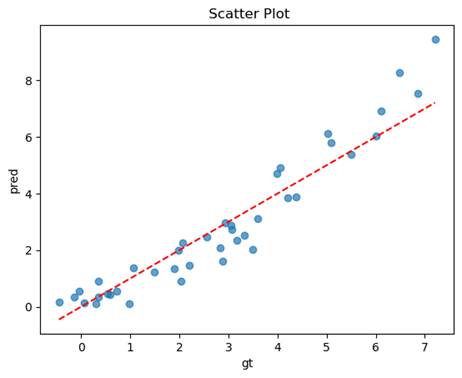
-
- 最小最大缩放
均方误差(MSE): 0.2554
决定系数(R2): 0.9419
问题讨论:
- 为什么数据集特征标准化对神经网络很重要?
神经网络的训练依赖于梯度下降算法,而特征标准化可以显著影响梯度下降的效率和稳定性。以下是标准化的重要原因:
1.加速收敛:特征值的范围较大时,梯度下降的更新步长会因特征值的差异而不均衡,导致收敛速度变慢。标准化将特征缩放到相同的尺度,使梯度更新更加平稳,从而加速收敛。
2.避免某些特征的主导作用:如果某些特征的数值范围远大于其他特征,它们会对损失函数的贡献更大,从而主导模型的训练过程。标准化可以平衡各特征的影响,使模型更公平地学习所有特征。
3.减少数值不稳定性:神经网络的计算中涉及大量的矩阵乘法和非线性激活函数。如果特征值范围过大,可能导致梯度爆炸或梯度消失问题,影响模型的训练效果。标准化可以缓解这些问题。
4.适配激活函数:许多激活函数(如 sigmoid 和 tanh)对输入范围较敏感,输入值过大或过小会导致梯度接近零,影响训练效果。标准化后的数据更适合这些激活函数。
- 不同预处理方法如何影响模型训练效果?
无预处理(原始数据):特征值范围较大时,梯度下降可能收敛缓慢,甚至无法收敛。适用仅在特征值范围接近且分布均匀时,原始数据可能表现良好。
标准化(StandardScaler):将特征缩放到均值为 0、标准差为 1 的范围,适合梯度下降优化的模型(如神经网络)。收敛速度快,损失函数下降平稳,模型性能较好。特征值分布接近正态分布时效果最佳,适合大多数神经网络任务。
最小最大缩放(MinMaxScaler):将特征缩放到 [0, 1] 范围,适合需要归一化输入的模型(如距离度量相关的模型)。收敛速度较快,但对异常值敏感,可能导致模型性能不稳定。适用于特征值分布偏态或范围较大时,适合需要固定范围输入的任务。
实验3:PyTorch实现MLP和CNN对CIFAR-10数据集分类
一、实验目的:
- 掌握使用PyTorch构建神经网络的方法
- 理解MLP和CNN在图像分类任务中的区别
- 了解和解决神经网络过拟合问题
二、实验结果:
- 代码一份
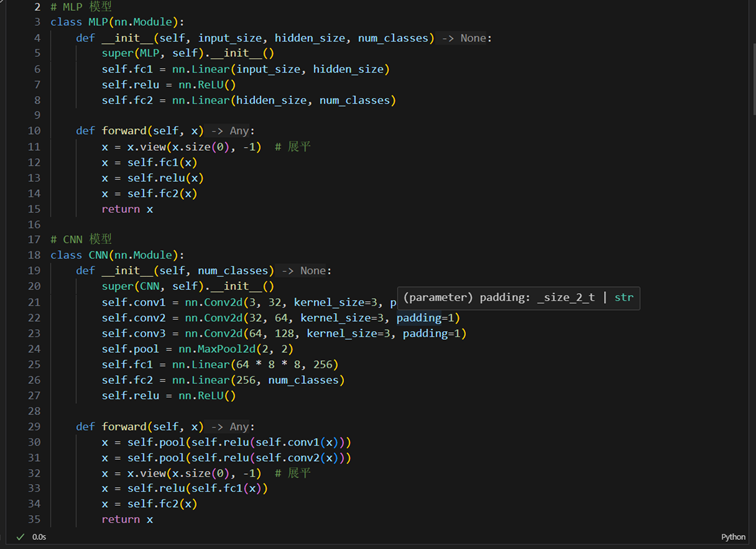
- 模型结构参数统计
|
模型 |
参数量 |
计算量(FLOPs) |
|
MLP |
1578506 |
3155968 |
|
CNN |
1144650 |
12257792 |
- 训练过程记录.
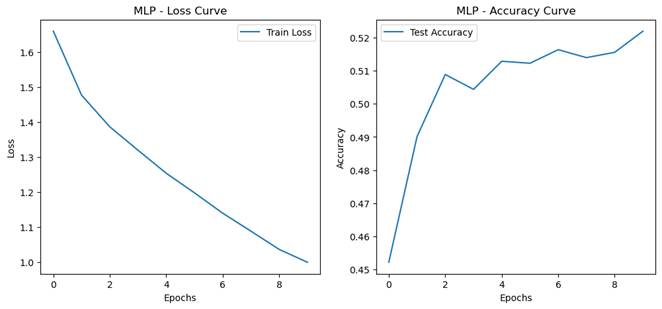
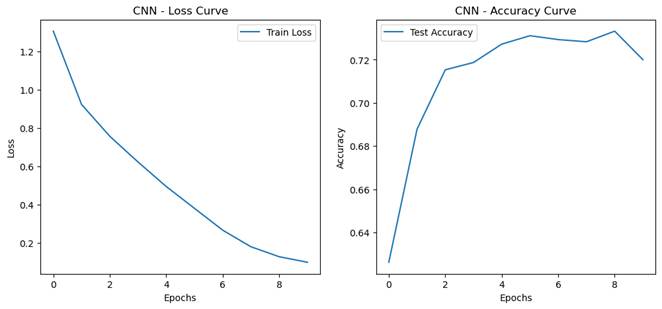
- 模型性能对比
|
模型 |
测试集准确率 |
训练时间 |
推理时间 |
|
MLP |
0.5220 |
2m 59.0s |
36.1s |
|
CNN |
0.7200 |
3m 16.2s |
39 3s |
三、实验讨论与分析
- MLP和CNN架构性能对比
实验要求:在相近参数量情况下比较两种模型,记录并分析性能差异。
通过实验记录的测试集准确率、训练时间和推理时间,可以验证以下结论:
测试集准确率:CNN 的准确率显著高于 MLP,尤其是在图像分类任务中。
训练时间:CNN 的训练时间可能略长于 MLP,但由于参数量较少,计算效率更高。
推理时间:CNN 的推理时间通常较短,适合实时应用。
问题讨论:在图像分类任务中,CNN相比MLP的优势体现在哪些方面?
1. 参数共享与稀疏连接
CNN:
卷积层中的卷积核(滤波器)通过参数共享机制,在整个输入图像上滑动,提取局部特征。每个卷积核只与局部区域连接(稀疏连接),大幅减少了参数量。这种机制使 CNN 能够高效地学习图像的空间特征,同时降低了过拟合风险。
MLP:
全连接层中的每个神经元与上一层的所有神经元相连(密集连接),导致参数量随输入维度线性增长。对于高维输入(如展平后的图像),参数量巨大,容易导致过拟合。
2. 空间信息的保留
CNN:卷积操作能够保留图像的空间结构(如像素之间的相对位置)。池化操作进一步提取特征的空间不变性(如平移不变性),使模型对图像的局部特征更加鲁棒。
MLP:输入图像在展平后,空间信息(如像素的相邻关系)被完全丢失。模型只能依赖全局特征,难以捕捉图像的局部模式。
3. 泛化能力
CNN:通过卷积核提取局部特征,具有较强的泛化能力。对图像的平移、缩放和旋转等变换具有鲁棒性。
MLP:由于参数量大且缺乏空间特征提取能力,MLP 更容易过拟合,泛化能力较弱。
4. 适用场景
CNN:专为图像数据设计,适合处理具有空间结构的输入(如图像、视频)。在图像分类、目标检测、语义分割等任务中表现优异。
MLP:更适合处理结构化数据(如表格数据)或低维特征输入。在图像分类任务中,性能通常不如 CNN。
实验结果分析
- 过拟合现象分析
实验要求:观察和分析过拟合现象
- 设计对比实验观察过拟合现象:
- 基准模型
- 增大模型 MLP hidden_size增大为1024,CNN增加一层卷积
- 延长训练轮数到20轮
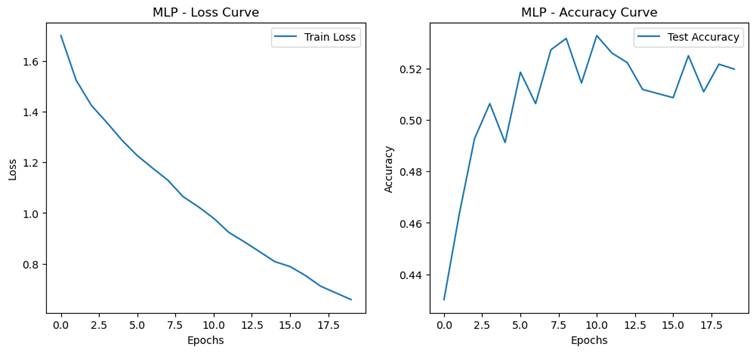
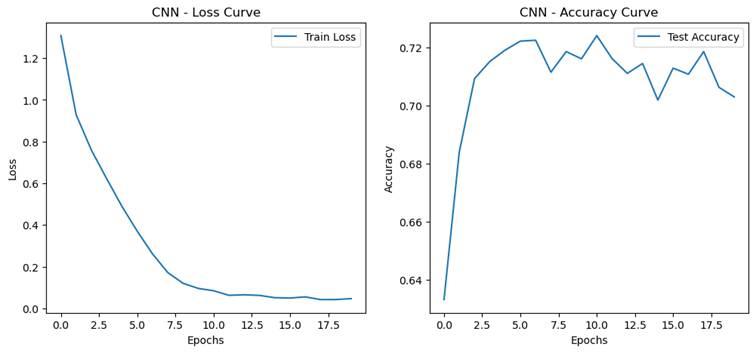
- 过拟合程度量化指标
- 训练集和测试集准确率的差距(泛化误差 = 训练集准确率 - 测试集准确率)
MLP:0.3803
CNN:0.2970
-
- 最佳验证性能出现的轮次/迭代次数(越早出现说明越容易过拟合)
MLP:10
CNN:10
问题讨论:
- 什么是过拟合?不同模型结构下,过拟合的表现形式有何不同?
过拟合是指模型在训练集上表现非常好(训练误差很低),但在测试集或验证集上表现较差(测试误差较高)的现象。过拟合通常发生在模型过于复杂、参数过多或训练数据不足的情况下,导致模型过度拟合训练数据中的噪声或细节,而无法很好地泛化到未见数据。
过拟合的特征:
- 训练集准确率高,但测试集准确率低。
- 训练误差持续下降,但测试误差在某一时刻开始上升。
- 泛化误差(训练集准确率与测试集准确率的差距)较大。
2. 不同模型结构下,过拟合的表现形式有何不同?
MLP(多层感知机):MLP 的参数量通常较大,尤其是输入维度较高时(如展平后的图像数据),容易导致过拟合。过拟合表现为训练集准确率迅速达到很高的水平,但测试集准确率停滞或下降。由于 MLP 缺乏空间特征提取能力,可能会过度拟合训练数据中的局部噪声。
CNN(卷积神经网络):CNN 通过卷积操作实现参数共享和稀疏连接,参数量相对较少,因此比 MLP 更不容易过拟合。过拟合的表现形式通常较为缓和,但在深层网络或小数据集上,仍可能出现训练集准确率远高于测试集准确率的情况。CNN 的过拟合可能更多地体现在对训练数据中特定模式的过度记忆,而不是对噪声的拟合。
- 如何缓解过拟合?
缓解过拟合的方法可以从模型设计、数据处理和训练策略三个方面入手:
(1) 模型设计
减少模型复杂度:
降低网络的层数或每层的神经元数量。
使用较小的卷积核或减少卷积层的通道数。
正则化:
使用 L1 或 L2 正则化(权重衰减)来限制模型的参数大小。
在 PyTorch 中,可以通过优化器的 weight_decay 参数实现:
Dropout:
在训练过程中随机丢弃部分神经元,减少神经元之间的依赖性。
在 PyTorch 中可以使用 nn.Dropout:
(2) 数据处理
数据增强:
通过旋转、翻转、裁剪、缩放等方式增加数据的多样性,减少模型对训练数据的过度依赖。
在 PyTorch 中可以使用 torchvision.transforms:
增加训练数据:
如果可能,收集更多的训练数据,尤其是多样性较高的数据。
(3) 训练策略
神经网络设计实验
段正昊
34520251151581
实验1:MLPClassifier构建神经网络完成手写数字分类
一、实验目的
1. 掌握使用sklearn机器学习库构建神经网络模型的方法
2. 理解多层感知器(MLP)在分类任务中的应用
3. 学习评估和优化神经网络模型性能的方法
二、实验步骤
- 数据集准备
- 加载MNIST数据集
- 数据预处理(归一化、划分训练集和测试集)
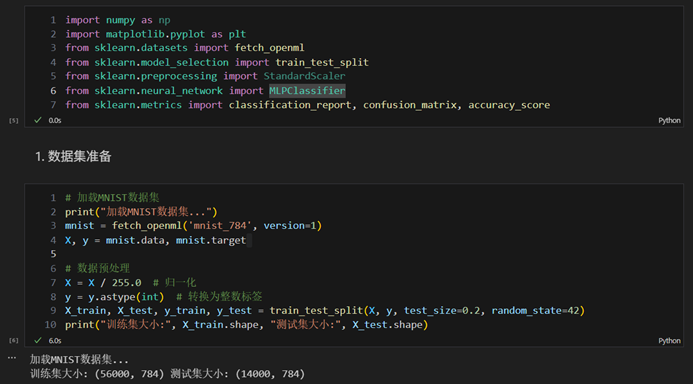
- 模型构建
- 设计网络结构(隐藏层大小、层数等)
- 设置模型参数(学习率、激活函数、优化器等)
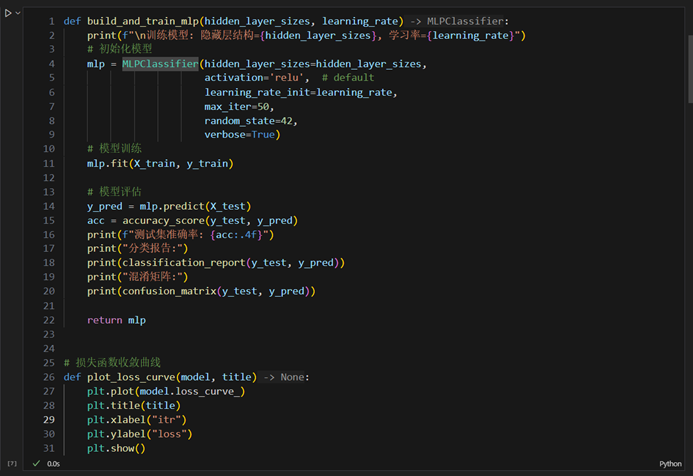
- 模型训练与测试
- 训练过程记录
- 测试集评估
三、实验结果
- 代码一份
- 训练过程分析
- 损失函数收敛曲线
- 模型性能评估
- 在测试集上的准确率
- 混淆矩阵
- 分类报告(准确率、召回率、F1分数)
四、实验讨论与分析
- 学习率影响分析
实验要求:尝试不同的学习率(0.1、0.01、0.001)对模型性能表现,并记录实验结果。

1.1训练模型: 隐藏层结构=(100,), 学习率=0.1
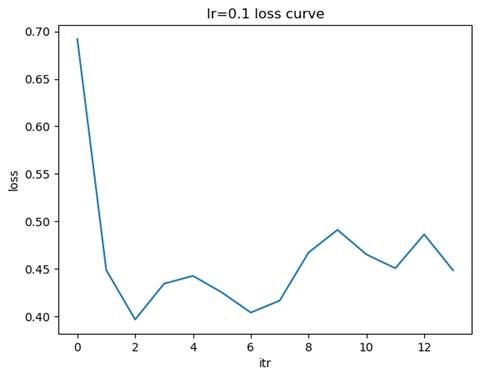
测试集准确率: 0.9054
混淆矩阵:
[[1272 0 1 0 1 0 8 2 57 2]
[ 0 1547 6 8 1 3 1 4 29 1]
[ 2 4 1271 4 7 0 8 4 77 3]
[ 4 0 55 1237 0 25 0 12 90 10]
[ 1 0 1 1 1138 4 5 5 79 61]
[ 3 4 1 48 9 1019 14 1 166 8]
[ 6 1 7 0 4 16 1304 0 58 0]
[ 7 3 51 1 2 0 0 1353 45 41]
[ 3 8 24 12 5 3 14 2 1282 4]
[ 4 3 0 13 19 0 1 26 102 1252]]
分类报告:
precision recall f1-score support
0 0.98 0.95 0.96 1343
1 0.99 0.97 0.98 1600
2 0.90 0.92 0.91 1380
3 0.93 0.86 0.90 1433
4 0.96 0.88 0.92 1295
5 0.95 0.80 0.87 1273
6 0.96 0.93 0.95 1396
7 0.96 0.90 0.93 1503
8 0.65 0.94 0.77 1357
9 0.91 0.88 0.89 1420
accuracy 0.91 14000
macro avg 0.92 0.90 0.91 14000
weighted avg 0.92 0.91 0.91 14000
-
- 训练模型: 隐藏层结构=(100,), 学习率=0.01
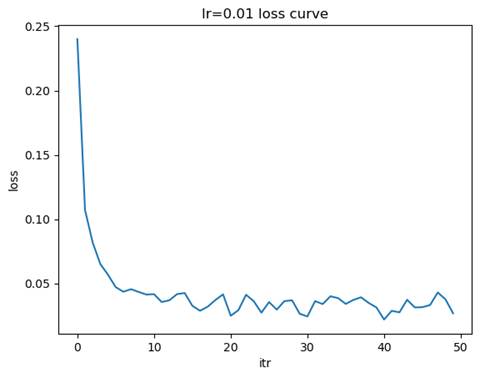
测试集准确率: 0.9750
混淆矩阵:
[[1325 0 4 0 1 1 3 1 7 1]
[ 0 1582 2 2 2 0 0 4 8 0]
[ 0 3 1352 0 1 2 3 2 16 1]
[ 2 2 19 1374 1 10 0 2 16 7]
[ 3 0 3 0 1252 0 4 4 8 21]
[ 2 3 1 11 1 1226 7 1 17 4]
[ 6 0 1 0 4 1 1370 0 14 0]
[ 1 3 12 2 5 1 0 1460 8 11]
[ 0 2 7 1 3 2 4 3 1332 3]
[ 3 3 2 3 9 2 0 7 14 1377]]
分类报告:
precision recall f1-score support
0 0.99 0.99 0.99 1343
1 0.99 0.99 0.99 1600
2 0.96 0.98 0.97 1380
3 0.99 0.96 0.97 1433
4 0.98 0.97 0.97 1295
5 0.98 0.96 0.97 1273
6 0.98 0.98 0.98 1396
7 0.98 0.97 0.98 1503
8 0.93 0.98 0.95 1357
9 0.97 0.97 0.97 1420
accuracy 0.97 14000
macro avg 0.98 0.97 0.97 14000
weighted avg 0.98 0.97 0.98 14000
-
- 训练模型: 隐藏层结构=(100,), 学习率=0.001
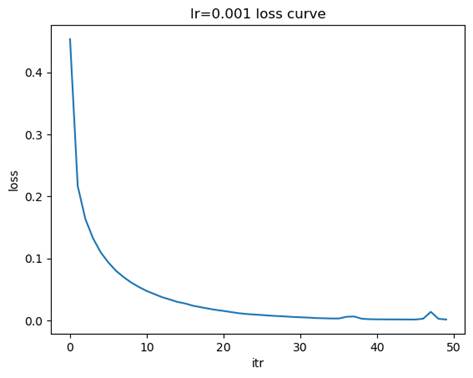
测试集准确率: 0.9751
混淆矩阵:
[[1324 1 2 0 0 0 5 3 5 3]
[ 0 1586 3 2 1 0 1 5 1 1]
[ 3 5 1331 4 2 3 6 7 16 3]
[ 0 1 16 1380 2 11 2 6 5 10]
[ 0 1 3 0 1265 0 2 2 3 19]
[ 1 2 0 16 3 1233 8 1 8 1]
[ 0 0 1 0 3 4 1385 1 2 0]
[ 1 3 13 2 3 2 0 1464 0 15]
[ 6 7 7 8 5 3 7 3 1303 8]
[ 5 4 1 5 12 4 0 3 6 1380]]
分类报告:
precision recall f1-score support
0 0.99 0.99 0.99 1343
1 0.99 0.99 0.99 1600
2 0.97 0.96 0.97 1380
3 0.97 0.96 0.97 1433
4 0.98 0.98 0.98 1295
5 0.98 0.97 0.97 1273
6 0.98 0.99 0.99 1396
7 0.98 0.97 0.98 1503
8 0.97 0.96 0.96 1357
9 0.96 0.97 0.97 1420
accuracy 0.98 14000
macro avg 0.97 0.97 0.97 14000
weighted avg 0.98 0.98 0.98 14000
问题讨论:
- 比较不同学习率下损失函数的收敛速度
学习率较大(如 0.1):损失函数的下降速度较快,但可能会出现震荡,甚至无法收敛。学习率适中(如 0.01):损失函数下降平稳,收敛速度适中,通常是较优的选择。学习率较小(如 0.001):损失函数下降非常缓慢但最平稳,可能需要更多的迭代次数才能达到收敛。
- 分析学习率过大和过小分别会导致什么问题
学习率过大模型可能无法收敛,损失函数在较高值附近震荡。
原因:每次梯度更新的步长过大,可能越过最优点。
现象:训练过程中的损失值波动较大,测试集准确率较低。
学习率过小模型收敛速度过慢,训练时间显著增加。
原因:每次梯度更新的步长过小,导致优化过程效率低下。
现象:损失函数下降缓慢,可能在有限的迭代次数内未达到最优点。
- 结合实验结果,讨论如何选择合适的学习率
学习率应在保证收敛稳定性的同时,尽可能加快收敛速度。通过实验观察,选择一个既能快速收敛又能稳定达到较低损失值的学习率。如果 0.1 学习率导致震荡,而 0.001 学习率收敛过慢,则 0.01 是一个较好的折中选择。可以结合损失函数曲线和测试集准确率,进一步验证选择的学习率是否合适。
在实际任务中,可以使用学习率调度器(如 learning_rate='adaptive')动态调整学习率。初始学习率可以从 0.01 开始,逐步尝试调整,找到适合当前任务的最佳值。
- 网络结构影响分析:
2.1隐藏层节点数量影响分析
实验要求:使用单隐藏层,尝试不同的节点数量(20、50、100、200),并记录实验结果。

2.1.1 训练模型: 隐藏层结构=(20,), 学习率=0.01
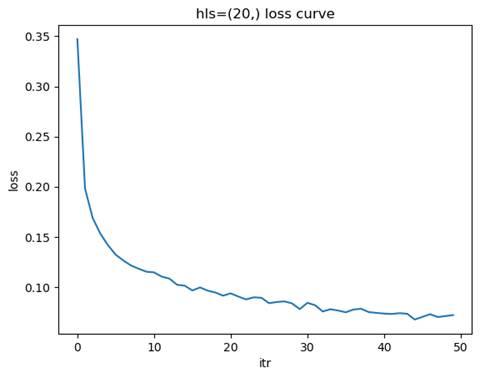
测试集准确率: 0.9461
混淆矩阵:
[[1307 0 3 0 1 7 10 6 8 1]
[ 1 1567 7 5 1 0 3 4 10 2]
[ 9 13 1285 13 13 3 8 11 23 2]
[ 1 15 29 1320 2 28 4 11 16 7]
[ 4 0 3 5 1219 5 7 7 6 39]
[ 6 9 0 26 2 1196 15 2 15 2]
[ 9 6 8 0 12 15 1341 0 3 2]
[ 11 6 15 5 3 7 0 1414 4 38]
[ 6 17 10 14 5 22 6 5 1257 15]
[ 7 7 1 7 16 13 0 11 19 1339]]
分类报告:
precision recall f1-score support
0 0.96 0.97 0.97 1343
1 0.96 0.98 0.97 1600
2 0.94 0.93 0.94 1380
3 0.95 0.92 0.93 1433
4 0.96 0.94 0.95 1295
5 0.92 0.94 0.93 1273
6 0.96 0.96 0.96 1396
7 0.96 0.94 0.95 1503
8 0.92 0.93 0.92 1357
9 0.93 0.94 0.93 1420
accuracy 0.95 14000
macro avg 0.95 0.95 0.95 14000
weighted avg 0.95 0.95 0.95 14000
2.1.2 训练模型: 隐藏层结构=(50,), 学习率=0.01
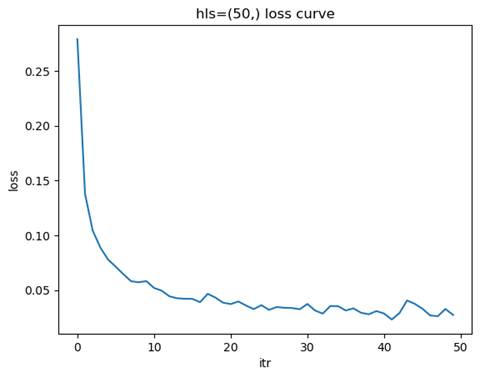
测试集准确率: 0.9651
混淆矩阵:
[[1314 0 3 0 4 3 3 3 8 5]
[ 0 1588 5 3 1 0 1 2 0 0]
[ 9 11 1323 10 5 0 2 8 7 5]
[ 1 5 18 1368 1 20 1 6 4 9]
[ 3 1 5 2 1239 1 6 2 0 36]
[ 7 4 1 19 4 1204 7 0 17 10]
[ 5 0 0 0 6 8 1371 0 6 0]
[ 3 4 17 4 4 0 1 1446 1 23]
[ 5 8 11 8 4 11 3 13 1284 10]
[ 4 6 1 8 8 2 0 11 6 1374]]
分类报告:
precision recall f1-score support
0 0.97 0.98 0.98 1343
1 0.98 0.99 0.98 1600
2 0.96 0.96 0.96 1380
3 0.96 0.95 0.96 1433
4 0.97 0.96 0.96 1295
5 0.96 0.95 0.95 1273
6 0.98 0.98 0.98 1396
7 0.97 0.96 0.97 1503
8 0.96 0.95 0.95 1357
9 0.93 0.97 0.95 1420
accuracy 0.97 14000
macro avg 0.97 0.96 0.96 14000
weighted avg 0.97 0.97 0.97 14000
2.1.3 训练模型: 隐藏层结构=(100,), 学习率=0.01
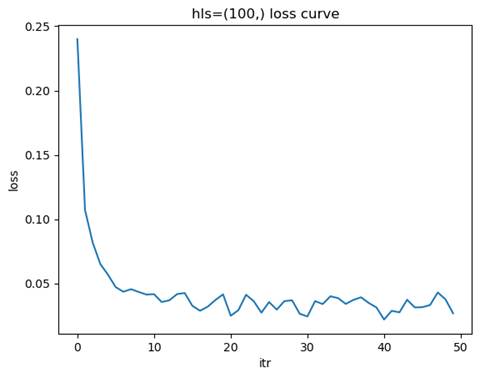
测试集准确率: 0.9750
分类报告:
precision recall f1-score support
0 0.99 0.99 0.99 1343
1 0.99 0.99 0.99 1600
2 0.96 0.98 0.97 1380
3 0.99 0.96 0.97 1433
4 0.98 0.97 0.97 1295
5 0.98 0.96 0.97 1273
6 0.98 0.98 0.98 1396
7 0.98 0.97 0.98 1503
8 0.93 0.98 0.95 1357
9 0.97 0.97 0.97 1420
accuracy 0.97 14000
macro avg 0.98 0.97 0.97 14000
weighted avg 0.98 0.97 0.98 14000
混淆矩阵:
[[1325 0 4 0 1 1 3 1 7 1]
[ 0 1582 2 2 2 0 0 4 8 0]
[ 0 3 1352 0 1 2 3 2 16 1]
[ 2 2 19 1374 1 10 0 2 16 7]
[ 3 0 3 0 1252 0 4 4 8 21]
[ 2 3 1 11 1 1226 7 1 17 4]
[ 6 0 1 0 4 1 1370 0 14 0]
[ 1 3 12 2 5 1 0 1460 8 11]
[ 0 2 7 1 3 2 4 3 1332 3]
[ 3 3 2 3 9 2 0 7 14 1377]]
2.1.4 训练模型: 隐藏层结构=(200,), 学习率=0.01
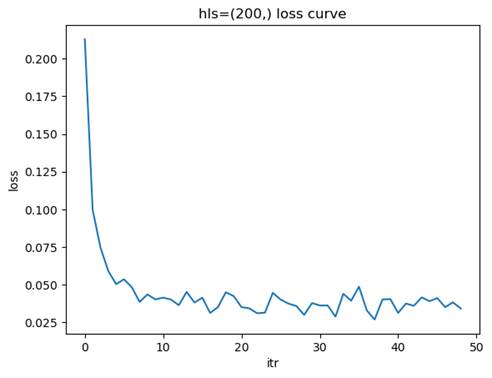
测试集准确率: 0.9758
分类报告:
precision recall f1-score support
0 0.98 0.99 0.98 1343
1 0.99 0.99 0.99 1600
2 0.97 0.98 0.97 1380
3 0.98 0.97 0.97 1433
4 0.98 0.97 0.98 1295
5 0.97 0.97 0.97 1273
6 0.98 0.98 0.98 1396
7 0.98 0.97 0.98 1503
8 0.96 0.97 0.96 1357
9 0.96 0.97 0.97 1420
accuracy 0.98 14000
macro avg 0.98 0.98 0.98 14000
weighted avg 0.98 0.98 0.98 14000
混淆矩阵:
[[1323 0 6 0 1 3 3 1 5 1]
[ 0 1582 2 5 1 0 0 3 6 1]
[ 2 4 1346 5 2 1 2 4 13 1]
[ 2 2 15 1387 0 12 0 2 8 5]
[ 2 2 0 0 1262 0 6 3 1 19]
[ 1 0 1 5 1 1241 10 0 12 2]
[ 3 1 0 0 5 7 1370 1 9 0]
[ 1 2 17 2 2 2 0 1453 3 21]
[ 7 3 5 5 4 2 3 3 1317 8]
[ 4 3 0 6 10 7 0 6 4 1380]]
问题讨论:节点数量如何影响模型的学习能力?
节点数量对模型的学习能力有着显著影响。节点数量较少时,模型的表达能力有限,无法捕捉数据中的复杂特征,容易导致欠拟合现象。这种情况下,训练集和测试集的准确率都较低,损失函数下降缓慢且可能在较高值附近收敛。随着节点数量的增加,模型的表达能力逐渐增强,能够更好地拟合数据中的特征,测试集准确率也随之提高,损失函数下降平稳且收敛速度适中。然而,当节点数量过多时,模型的复杂度过高,可能会导致过拟合问题,表现为训练集准确率很高,但测试集准确率下降,泛化能力变差,同时训练时间和计算资源的需求也会显著增加。
因此,选择合适的节点数量需要综合考虑数据的复杂度和规模。如果数据特征较为复杂或数据量较大,可以适当增加节点数量以增强模型的表达能力;而对于简单数据或数据量较少的情况,应减少节点数量以避免过拟合。通过实验验证不同节点数量下的模型性能,观察测试集准确率和损失函数的变化,可以帮助找到欠拟合与过拟合之间的平衡点,从而选择最优的节点数量。
2.2层结构影响分析:
实验要求:保持总参数量相近(约1万个参数),尝试不同的层结构并记录实验结果。
- 窄而深:(20,20,20,20)
- 金字塔形:(100,50,25)
- 倒金字塔形:(25,50,100)
- 宽而浅:(100,)
-
-
- 训练模型: 隐藏层结构=(20, 20, 20, 20), 学习率=0.01
-
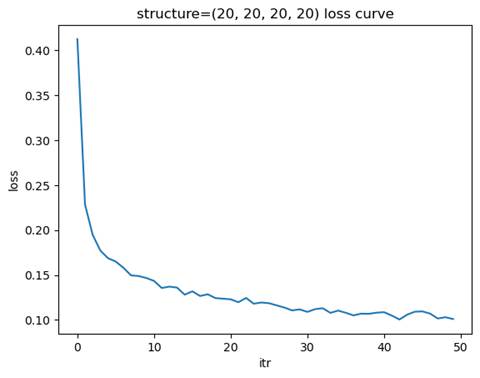
测试集准确率: 0.9468
混淆矩阵:
[[1305 0 10 0 1 2 6 1 12 6]
[ 0 1561 14 2 4 1 1 6 10 1]
[ 5 1 1323 9 10 2 8 11 9 2]
[ 1 1 21 1319 1 24 3 21 32 10]
[ 7 1 11 0 1251 0 3 4 3 15]
[ 3 3 8 30 9 1178 5 4 24 9]
[ 11 2 12 0 6 15 1339 1 10 0]
[ 4 2 21 2 10 1 0 1447 1 15]
[ 7 10 16 11 7 9 3 6 1278 10]
[ 5 3 1 9 91 2 0 35 20 1254]]
分类报告:
precision recall f1-score support
0 0.97 0.97 0.97 1343
1 0.99 0.98 0.98 1600
2 0.92 0.96 0.94 1380
3 0.95 0.92 0.94 1433
4 0.90 0.97 0.93 1295
5 0.95 0.93 0.94 1273
6 0.98 0.96 0.97 1396
7 0.94 0.96 0.95 1503
8 0.91 0.94 0.93 1357
9 0.95 0.88 0.91 1420
accuracy 0.95 14000
macro avg 0.95 0.95 0.95 14000
weighted avg 0.95 0.95 0.95 14000
-
-
- 训练模型: 隐藏层结构=(100, 50, 25), 学习率=0.01
-
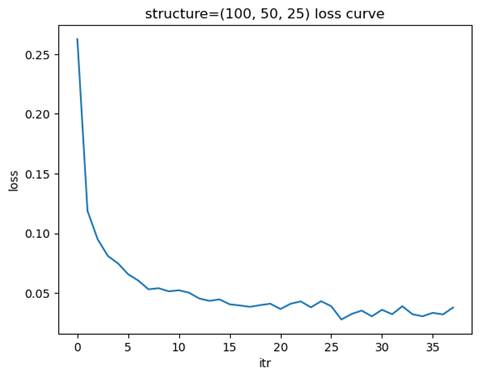
测试集准确率: 0.9727
混淆矩阵:
[[1329 1 2 0 1 0 1 0 8 1]
[ 0 1584 3 2 2 0 1 6 2 0]
[ 5 6 1341 6 5 0 0 6 8 3]
[ 1 1 11 1378 0 12 0 10 19 1]
[ 2 0 3 1 1253 1 3 2 10 20]
[ 2 1 0 10 1 1231 12 1 13 2]
[ 2 1 3 0 3 8 1373 0 5 1]
[ 2 5 11 1 0 3 0 1472 4 5]
[ 4 9 6 4 5 7 3 5 1311 3]
[ 6 3 0 6 12 5 1 18 23 1346]]
分类报告:
precision recall f1-score support
0 0.98 0.99 0.99 1343
1 0.98 0.99 0.99 1600
2 0.97 0.97 0.97 1380
3 0.98 0.96 0.97 1433
4 0.98 0.97 0.97 1295
5 0.97 0.97 0.97 1273
6 0.98 0.98 0.98 1396
7 0.97 0.98 0.97 1503
8 0.93 0.97 0.95 1357
9 0.97 0.95 0.96 1420
accuracy 0.97 14000
macro avg 0.97 0.97 0.97 14000
weighted avg 0.97 0.97 0.97 14000
-
-
- 训练模型: 隐藏层结构=(25, 50, 100), 学习率=0.01
-
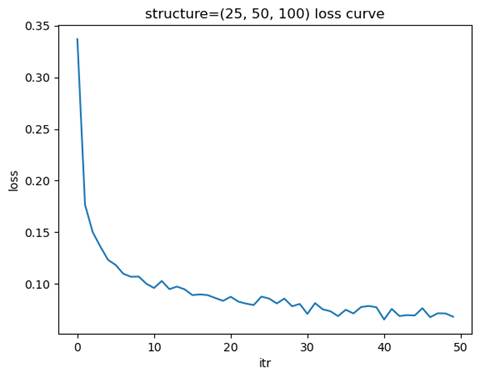
测试集准确率: 0.9590
混淆矩阵:
[[1312 1 3 1 2 7 9 0 7 1]
[ 0 1580 1 5 2 0 1 3 7 1]
[ 2 4 1330 6 4 5 3 9 15 2]
[ 0 1 15 1376 1 9 2 6 13 10]
[ 2 0 5 0 1242 1 13 4 3 25]
[ 4 2 6 40 2 1182 19 0 12 6]
[ 8 1 2 0 9 9 1362 0 5 0]
[ 4 4 19 4 12 4 0 1431 7 18]
[ 6 7 16 21 5 12 8 4 1267 11]
[ 4 5 1 5 39 4 1 10 7 1344]]
分类报告:
precision recall f1-score support
0 0.98 0.98 0.98 1343
1 0.98 0.99 0.99 1600
2 0.95 0.96 0.96 1380
3 0.94 0.96 0.95 1433
4 0.94 0.96 0.95 1295
5 0.96 0.93 0.94 1273
6 0.96 0.98 0.97 1396
7 0.98 0.95 0.96 1503
8 0.94 0.93 0.94 1357
9 0.95 0.95 0.95 1420
accuracy 0.96 14000
macro avg 0.96 0.96 0.96 14000
weighted avg 0.96 0.96 0.96 14000
-
-
- 训练模型: 隐藏层结构=(100,), 学习率=0.01
-
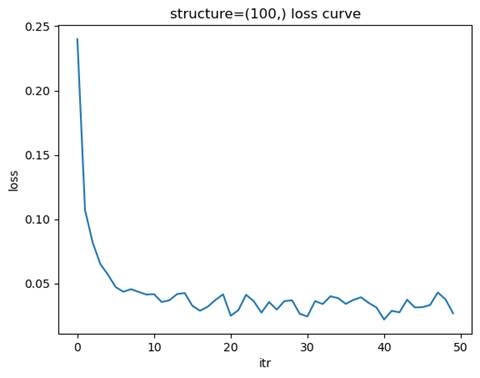
测试集准确率: 0.9750
混淆矩阵:
[[1325 0 4 0 1 1 3 1 7 1]
[ 0 1582 2 2 2 0 0 4 8 0]
[ 0 3 1352 0 1 2 3 2 16 1]
[ 2 2 19 1374 1 10 0 2 16 7]
[ 3 0 3 0 1252 0 4 4 8 21]
[ 2 3 1 11 1 1226 7 1 17 4]
[ 6 0 1 0 4 1 1370 0 14 0]
[ 1 3 12 2 5 1 0 1460 8 11]
[ 0 2 7 1 3 2 4 3 1332 3]
[ 3 3 2 3 9 2 0 7 14 1377]]
分类报告:
precision recall f1-score support
0 0.99 0.99 0.99 1343
1 0.99 0.99 0.99 1600
2 0.96 0.98 0.97 1380
3 0.99 0.96 0.97 1433
4 0.98 0.97 0.97 1295
5 0.98 0.96 0.97 1273
6 0.98 0.98 0.98 1396
7 0.98 0.97 0.98 1503
8 0.93 0.98 0.95 1357
9 0.97 0.97 0.97 1420
accuracy 0.97 14000
macro avg 0.98 0.97 0.97 14000
weighted avg 0.98 0.97 0.98 14000
问题讨论:哪种网络结构最合适?在保持参数量相近的情况下,层数和宽度如何权衡?
选择金字塔型结构最合适,其在较少的迭代次数下达到了近似最优的测试集准确率。
在保持参数量相近的情况下,网络结构的层数和宽度需要根据任务的复杂性和数据特征进行权衡。不同的网络结构(如窄而深、宽而浅、金字塔形、倒金字塔形)各有优劣,适合不同的应用场景。
窄而深的网络结构(如 (20, 20, 20, 20))通过增加层数来捕捉数据的复杂特征,适合处理具有高度非线性关系的数据。这种结构能够逐层提取特征,但训练时间较长,且可能面临梯度消失或梯度爆炸的问题,需要更好的优化器和正则化方法来稳定训练。
宽而浅的网络结构(如 (100,))通过增加每层的节点数量来增强模型的表达能力,适合处理简单或中等复杂度的数据。这种结构训练速度较快,但可能无法充分提取深层次特征,容易在复杂任务中表现不足。
金字塔形结构(如 (100, 50, 25))通过逐层减少节点数量,能够在前层提取更多的全局特征,后层逐步聚焦于更具体的特征。这种结构在许多任务中表现良好,兼顾了特征提取能力和计算效率。
倒金字塔形结构(如 (25, 50, 100))通过逐层增加节点数量,适合需要逐步扩展特征空间的任务,但在大多数情况下,这种结构的表现不如金字塔形或窄而深的结构。
在权衡层数和宽度时,需要考虑以下因素:数据的复杂性、训练数据量和计算资源。如果数据复杂且训练数据量充足,可以选择窄而深或金字塔形结构以增强特征提取能力;如果数据简单或计算资源有限,可以选择宽而浅的结构以提高训练效率。最终,最合适的网络结构通常需要通过实验验证,结合测试集的准确率、损失函数的收敛情况以及模型的泛化能力来确定。
实验2:MLPRegressor构建神经网络预测学生成绩
一、实验目的
掌握神经网络在回归任务中的应用方法
熟悉基本的数据预处理方法
二、实验结果
- 代码一份
- 训练过程分析
损失函数收敛曲线
- 模型性能评估
均方误差(MSE)
决定系数(R2)
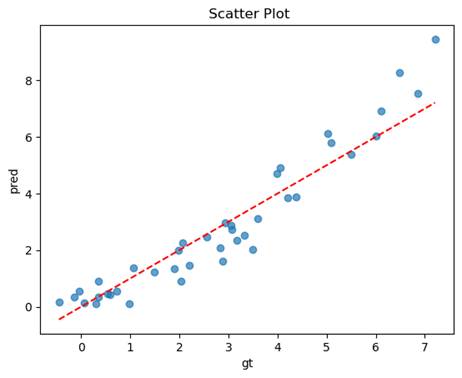
预测值与真实值的散点图
三、实验讨论与分析
- 不同特征对模型预测的影响分析
实验要求:分析不同特征对预测结果的影响
原始 MSE: 0.2219
特征 Feature 1 置零后 MSE: 3.1137,变化: 2.8919
特征 Feature 2 置零后 MSE: 1.7032,变化: 1.4813
特征 Feature 3 置零后 MSE: 0.5121,变化: 0.2902
特征 Feature 4 置零后 MSE: 0.3769,变化: 0.1550
特征 Feature 5 置零后 MSE: 4.0887,变化: 3.8669
问题讨论:哪类特征对预测学生成绩最重要?为什么?
当某个特征被置零后,MSE 的变化量越大,说明该特征对模型预测的贡献越大。如果置零某个特征后,MSE 几乎没有变化,说明该特征对模型预测的影响较小,可能是一个冗余特征。
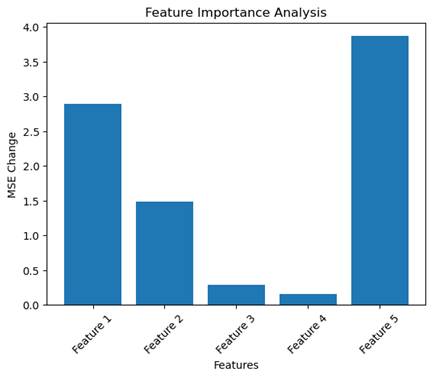
特征 Feature 5 的 MSE 变化最大(3.8669),说明它对模型预测最重要。特征 Feature 1 的 MSE 变化次大(2.8919),说明它也是一个关键特征。特征 Feature 2 的 MSE 变化为 1.4813,说明它对预测有一定影响,但不如 Feature 1 和 Feature 5。特征 Feature 3 和 Feature 4 的 MSE 变化较小(分别为 0.2902 和 0.1550),说明它们对模型预测的贡献较低。
- 数据预处理方式对比分析
实验要求; 对比不同预处理方法对模型性能的影响,并记录实验结果
- 无预处理(原始数据)
- 标准化(StandardScaler):减均值除方差
- 最小最大缩放(MinMaxScaler):缩放到[0,1]区间
-
- 无预处理
均方误差(MSE): 0.2470
决定系数(R2): 0.9438
-
- 标准化
均方误差(MSE): 0.5784
决定系数(R2): 0.8685
-
- 最小最大缩放
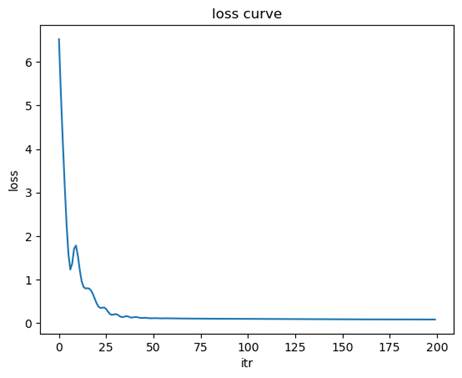
均方误差(MSE): 0.2554
决定系数(R2): 0.9419
问题讨论:
- 为什么数据集特征标准化对神经网络很重要?
神经网络的训练依赖于梯度下降算法,而特征标准化可以显著影响梯度下降的效率和稳定性。以下是标准化的重要原因:
1.加速收敛:特征值的范围较大时,梯度下降的更新步长会因特征值的差异而不均衡,导致收敛速度变慢。标准化将特征缩放到相同的尺度,使梯度更新更加平稳,从而加速收敛。
2.避免某些特征的主导作用:如果某些特征的数值范围远大于其他特征,它们会对损失函数的贡献更大,从而主导模型的训练过程。标准化可以平衡各特征的影响,使模型更公平地学习所有特征。
3.减少数值不稳定性:神经网络的计算中涉及大量的矩阵乘法和非线性激活函数。如果特征值范围过大,可能导致梯度爆炸或梯度消失问题,影响模型的训练效果。标准化可以缓解这些问题。
4.适配激活函数:许多激活函数(如 sigmoid 和 tanh)对输入范围较敏感,输入值过大或过小会导致梯度接近零,影响训练效果。标准化后的数据更适合这些激活函数。
- 不同预处理方法如何影响模型训练效果?
无预处理(原始数据):特征值范围较大时,梯度下降可能收敛缓慢,甚至无法收敛。适用仅在特征值范围接近且分布均匀时,原始数据可能表现良好。
标准化(StandardScaler):将特征缩放到均值为 0、标准差为 1 的范围,适合梯度下降优化的模型(如神经网络)。收敛速度快,损失函数下降平稳,模型性能较好。特征值分布接近正态分布时效果最佳,适合大多数神经网络任务。
最小最大缩放(MinMaxScaler):将特征缩放到 [0, 1] 范围,适合需要归一化输入的模型(如距离度量相关的模型)。收敛速度较快,但对异常值敏感,可能导致模型性能不稳定。适用于特征值分布偏态或范围较大时,适合需要固定范围输入的任务。
实验3:PyTorch实现MLP和CNN对CIFAR-10数据集分类
一、实验目的:
- 掌握使用PyTorch构建神经网络的方法
- 理解MLP和CNN在图像分类任务中的区别
- 了解和解决神经网络过拟合问题
二、实验结果:
- 代码一份
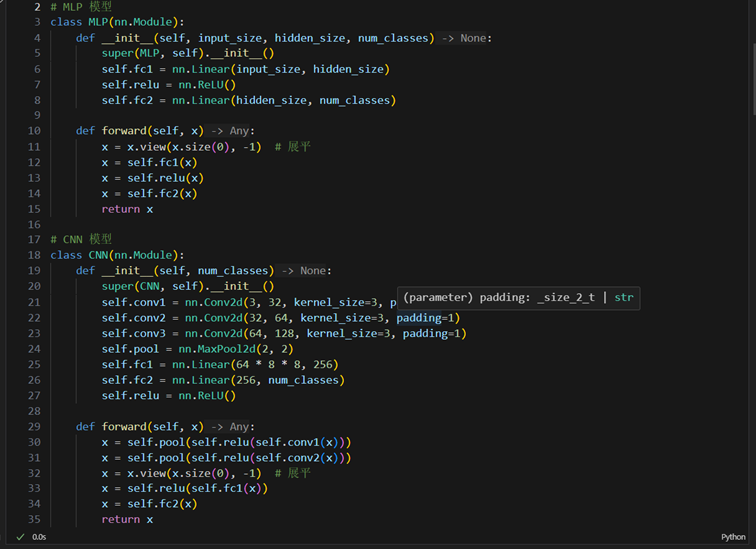
- 模型结构参数统计
|
模型 |
参数量 |
计算量(FLOPs) |
|
MLP |
1578506 |
3155968 |
|
CNN |
1144650 |
12257792 |
- 训练过程记录.
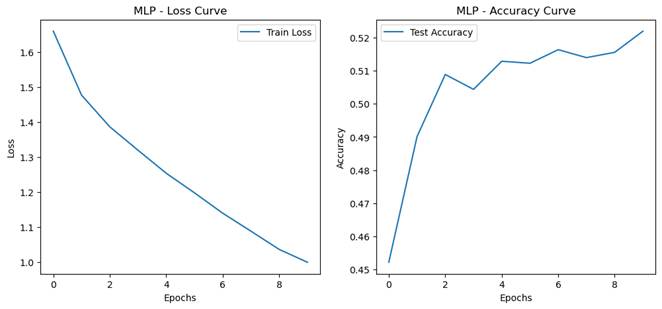
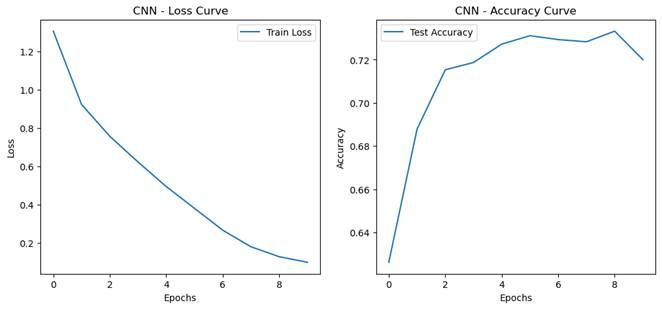
- 模型性能对比
|
模型 |
测试集准确率 |
训练时间 |
推理时间 |
|
MLP |
0.5220 |
2m 59.0s |
36.1s |
|
CNN |
0.7200 |
3m 16.2s |
39 3s |
三、实验讨论与分析
- MLP和CNN架构性能对比
实验要求:在相近参数量情况下比较两种模型,记录并分析性能差异。
通过实验记录的测试集准确率、训练时间和推理时间,可以验证以下结论:
测试集准确率:CNN 的准确率显著高于 MLP,尤其是在图像分类任务中。
训练时间:CNN 的训练时间可能略长于 MLP,但由于参数量较少,计算效率更高。
推理时间:CNN 的推理时间通常较短,适合实时应用。
问题讨论:在图像分类任务中,CNN相比MLP的优势体现在哪些方面?
1. 参数共享与稀疏连接
CNN:
卷积层中的卷积核(滤波器)通过参数共享机制,在整个输入图像上滑动,提取局部特征。每个卷积核只与局部区域连接(稀疏连接),大幅减少了参数量。这种机制使 CNN 能够高效地学习图像的空间特征,同时降低了过拟合风险。
MLP:
全连接层中的每个神经元与上一层的所有神经元相连(密集连接),导致参数量随输入维度线性增长。对于高维输入(如展平后的图像),参数量巨大,容易导致过拟合。
2. 空间信息的保留
CNN:卷积操作能够保留图像的空间结构(如像素之间的相对位置)。池化操作进一步提取特征的空间不变性(如平移不变性),使模型对图像的局部特征更加鲁棒。
MLP:输入图像在展平后,空间信息(如像素的相邻关系)被完全丢失。模型只能依赖全局特征,难以捕捉图像的局部模式。
3. 泛化能力
CNN:通过卷积核提取局部特征,具有较强的泛化能力。对图像的平移、缩放和旋转等变换具有鲁棒性。
MLP:由于参数量大且缺乏空间特征提取能力,MLP 更容易过拟合,泛化能力较弱。
4. 适用场景
CNN:专为图像数据设计,适合处理具有空间结构的输入(如图像、视频)。在图像分类、目标检测、语义分割等任务中表现优异。
MLP:更适合处理结构化数据(如表格数据)或低维特征输入。在图像分类任务中,性能通常不如 CNN。
实验结果分析
- 过拟合现象分析
实验要求:观察和分析过拟合现象
- 设计对比实验观察过拟合现象:
- 基准模型
- 增大模型 MLP hidden_size增大为1024,CNN增加一层卷积
- 延长训练轮数到20轮
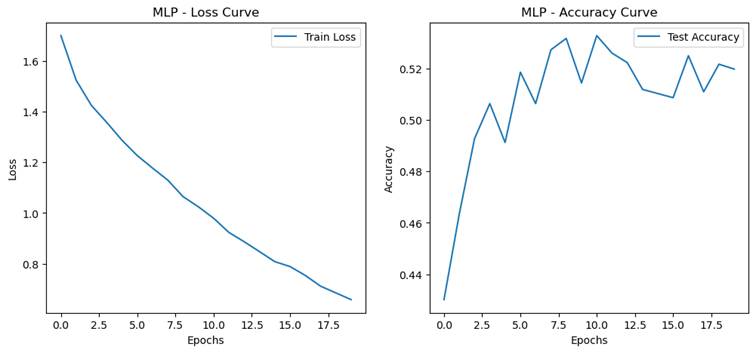
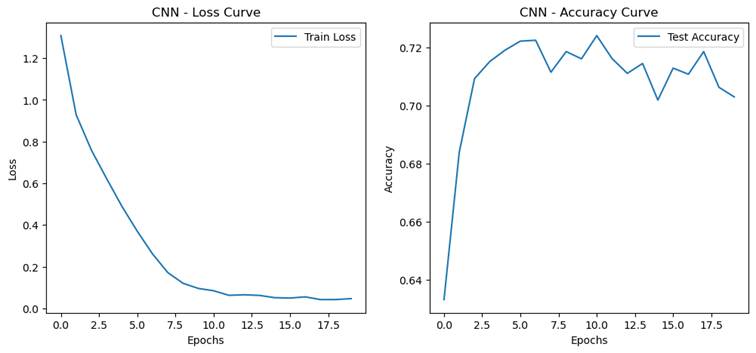
- 过拟合程度量化指标
- 训练集和测试集准确率的差距(泛化误差 = 训练集准确率 - 测试集准确率)
MLP:0.3803
CNN:0.2970
-
- 最佳验证性能出现的轮次/迭代次数(越早出现说明越容易过拟合)
MLP:10
CNN:10
问题讨论:
- 什么是过拟合?不同模型结构下,过拟合的表现形式有何不同?
过拟合是指模型在训练集上表现非常好(训练误差很低),但在测试集或验证集上表现较差(测试误差较高)的现象。过拟合通常发生在模型过于复杂、参数过多或训练数据不足的情况下,导致模型过度拟合训练数据中的噪声或细节,而无法很好地泛化到未见数据。
过拟合的特征:
- 训练集准确率高,但测试集准确率低。
- 训练误差持续下降,但测试误差在某一时刻开始上升。
- 泛化误差(训练集准确率与测试集准确率的差距)较大。
2. 不同模型结构下,过拟合的表现形式有何不同?
MLP(多层感知机):MLP 的参数量通常较大,尤其是输入维度较高时(如展平后的图像数据),容易导致过拟合。过拟合表现为训练集准确率迅速达到很高的水平,但测试集准确率停滞或下降。由于 MLP 缺乏空间特征提取能力,可能会过度拟合训练数据中的局部噪声。
CNN(卷积神经网络):CNN 通过卷积操作实现参数共享和稀疏连接,参数量相对较少,因此比 MLP 更不容易过拟合。过拟合的表现形式通常较为缓和,但在深层网络或小数据集上,仍可能出现训练集准确率远高于测试集准确率的情况。CNN 的过拟合可能更多地体现在对训练数据中特定模式的过度记忆,而不是对噪声的拟合。
- 如何缓解过拟合?
缓解过拟合的方法可以从模型设计、数据处理和训练策略三个方面入手:
(1) 模型设计
减少模型复杂度:
降低网络的层数或每层的神经元数量。
使用较小的卷积核或减少卷积层的通道数。
正则化:
使用 L1 或 L2 正则化(权重衰减)来限制模型的参数大小。
在 PyTorch 中,可以通过优化器的 weight_decay 参数实现:
Dropout:
在训练过程中随机丢弃部分神经元,减少神经元之间的依赖性。
在 PyTorch 中可以使用 nn.Dropout:
(2) 数据处理
数据增强:
通过旋转、翻转、裁剪、缩放等方式增加数据的多样性,减少模型对训练数据的过度依赖。
在 PyTorch 中可以使用 torchvision.transforms:
增加训练数据:
如果可能,收集更多的训练数据,尤其是多样性较高的数据。
(3) 训练策略
早停(Early Stopping):
在验证集性能不再提升时停止训练,避免模型过度拟合训练数据。
可以通过监控验证集损失实现。
降低学习率:
使用学习率调度器(如 ReduceLROnPlateau)在训练后期降低学习率,避免模型过度拟合。
在 PyTorch 中可以使用:
批量归一化(Batch Normalization):
对每一批数据进行归一化,稳定训练过程,减少过拟合风险。
早停(Early Stopping):
在验证集性能不再提升时停止训练,避免模型过度拟合训练数据。
可以通过监控验证集损失实现。
降低学习率:
使用学习率调度器(如 ReduceLROnPlateau)在训练后期降低学习率,避免模型过度拟合。
在 PyTorch 中可以使用:
批量归一化(Batch Normalization):
对每一批数据进行归一化,稳定训练过程,减少过拟合风险。






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








