POJ2411——Mondriaan's Dream

最新推荐文章于 2025-03-30 11:00:00 发布

tokers

最新推荐文章于 2025-03-30 11:00:00 发布

阅读量707

点赞数

CC 4.0 BY-SA版权

分类专栏： POJ 之旅 DP 文章标签： dp

本文链接：https://blog.youkuaiyun.com/Guard_Mine/article/details/40438355

DP 同时被 2 个专栏收录

194 篇文章

订阅专栏

POJ 之旅

175 篇文章

订阅专栏

本文详细介绍了使用状压DP方法解决Mondriaan's Dream问题的过程，涉及矩形填充的多种放置方案计算。通过DFS预处理状态，实现高效计算不同方式填充给定矩形的方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Mondriaan's Dream

Time Limit: 3000MS		Memory Limit: 65536K
Total Submissions: 12042		Accepted: 7011

Description

Squares and rectangles fascinated the famous Dutch painter Piet Mondriaan. One night, after producing the drawings in his 'toilet series' (where he had to use his toilet paper to draw on, for all of his paper was filled with squares and rectangles), he dreamt of filling a large rectangle with small rectangles of width 2 and height 1 in varying ways.

Expert as he was in this material, he saw at a glance that he'll need a computer to calculate the number of ways to fill the large rectangle whose dimensions were integer values, as well. Help him, so that his dream won't turn into a nightmare!

Input

The input contains several test cases. Each test case is made up of two integer numbers: the height h and the width w of the large rectangle. Input is terminated by h=w=0. Otherwise, 1<=h,w<=11.

Output

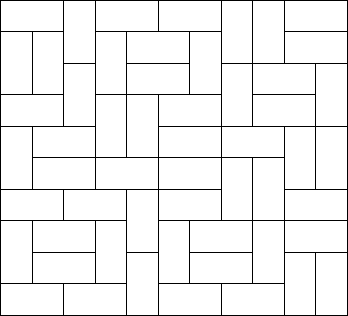For each test case, output the number of different ways the given rectangle can be filled with small rectangles of size 2 times 1. Assume the given large rectangle is oriented, i.e. count symmetrical tilings multiple times.

Sample Input

Sample Output

Source

覆盖模型，用状压dp解决

设棋盘为n, m为了高效起见，如果n > m，就交换，如果n, m都是奇数，答案一定是0（无论放多少牌，牌所占的空间是偶数的，所以最后的空间一定是偶数才能放满

dp[0][(1<<m)-1] = 1;

dp[i][j] += dp[i - 1][k];

其中的j和k是符合条件的状态，我们通过dfs预处理出来（把上一行和这一行的状态和在一起看做一个状态）

放置方案有3种，竖放，横放，不放（0）如果当前行当前列为0（二进制表示状态），那么当前列上一行一定是1（否则就空出2个位置来了）；如果当前行当前列为1，那么可能是竖放，则上一行当前列是0；可能是横放，则当前行下一列是1，上一行当前列是1，上一行下一列是1

为什么竖直放置要看做01呢，这样可以保证最后一行一定全部是1

#include <map>  
#include <set>  
#include <list>  
#include <stack>  
#include <vector>  
#include <queue>  
#include <cmath>  
#include <cstdio>  
#include <cstring>  
#include <iostream>  
#include <algorithm>  

using namespace std;

__int64 dp[12][2100];

struct node
{
    int cur, last;
}s[14000];

int n, m, res;

void dfs(int l, int cur, int last)
{
    if (l > m)
    {
        return ;
    }
    if (l == m)
    {
        s[res].cur = cur;
        s[res++].last = last;
        return;
    }
    dfs(l + 2, (cur << 2) | 3, (last << 2) | 3);
    dfs(l + 1, (cur << 1) | 1, last << 1);
    dfs(l + 1, (cur << 1), (last << 1) | 1);
}

int main()
{
    while (~scanf("%d%d", &n, &m))
    {
        if (!m && !n)
        {
            break;
        }
        if( (m & 1) && ( n & 1) )
        {
            printf("0\n");
            continue;
        }
        if (n < m)
        {
            m ^= n;
            n ^= m;
            m ^= n;
        }
        res = 0;
        dfs(0, 0, 0);
        memset (dp, 0, sizeof(dp) );
        dp[0][(1 << m) - 1] = 1;//作为初始化，第0行只能横放，因为不能影响下面；
        for (int i = 1; i <= n; ++i)
        {
            for (int j = 0; j < res; ++j)
            {
                dp[i][s[j].cur] += dp[i - 1][s[j].last];
            }
        }
        printf("%I64d\n", dp[n][(1 << m) - 1]);
    }
}