Educational Codeforces Round 85 C.Circle of Monsters 贪心

最新推荐文章于 2025-12-29 10:49:13 发布

原创最新推荐文章于 2025-12-29 10:49:13 发布 · 191 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#贪心算法

codeforces 专栏收录该内容

12 篇文章

订阅专栏

本文提出了一种针对特定射击游戏的优化策略：通过枚举起点并跟踪后续步骤来最小化总消耗，确保每次射击的成本尽可能低。关键在于计算每一步能够节省的最大成本，并找到重新开始的最佳时机。

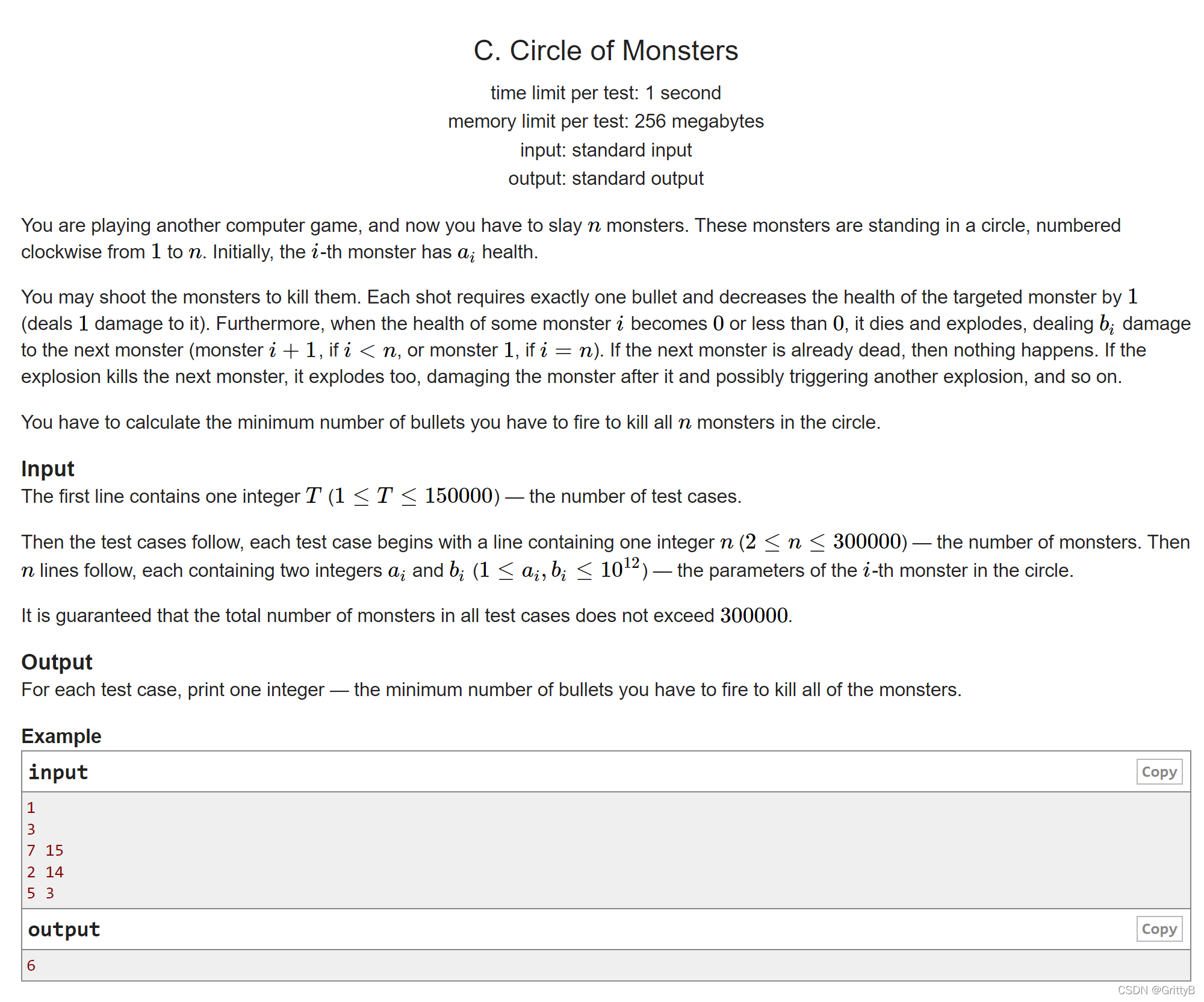
在这里插入图片描述

最朴素的想法，枚举开始的点，一直按顺序往下（因为每次射击一个，总的花费是总a[i] - 能够节省的b[i] ,在顺序的情况下，只有一个b[i]被浪费），每个点如果都被前bi-1影响，总花费就是所有的 max(a[i]-b[i-1],0), 断掉的地方，即让起始的地方增加量最小即可
找min a[i] - max(a[i]-b[i-1],0)

const int N = 3e5+10;

ll a[N], b[N];

void sov(){
    ll n;
    cin >> n;
    For(i, 1, n) {
        scanf("%lld%lld", &a[i], &b[i]);
    }
    ll al = 0;
    ll minz = 1e18;
    For(i,2,n){
        ll co = (b[i - 1] >= a[i] ? 0 : a[i] - b[i-1]);
        al += co;
        minz = min(minz, a[i]-co);
    }
    ll co = (b[n] >= a[1] ? 0 : a[1] - b[n]);
    al += co;
    minz = min(minz, a[1]-co);
    cout << al+minz << endl;
}

signed main(){
    #ifndef ONLINE_JUDGE
    freopen("in.txt","r",stdin);
    #endif
    
    int T;
    cin >> T;
    while(T--){
        sov();
    }
    return 0;
}