F Infinity Tree 找规律
题意
每次给定一个参数k,刚开始有一个树节点,每一秒钟,每个节点会长出k个子节点,给定u和v,求出u和v的lca。
思路
经过 x 秒, 总结点数 f(x)=(k+1)(x−1)f(x) = (k + 1 ) ^ (x - 1)f(x)=(k+1)(x−1)
指数级增长, 也就是说, 链长不会超过 64
t 号节点的父亲fa[t]=ceil((t−mx)/k)fa[t] = ceil ( (t - mx) / k )fa[t]=ceil((t−mx)/k) mx 是严格小于t 的最大f(x)
然后两边不断的向上找就好
code
void sov() {
ll k, x, y;
cin >> k >> x >> y;
ll xx = 1, yy = 1;
for(; xx < (ll)ceil(1.0 * x / (k + 1)); xx *= (k + 1); // 除法避免爆ll
for(; yy < (ll)ceil(1.0 * y / (k + 1)); yy *= (k + 1));
while(x != y) {
if(x > y) {
x = (x - xx + k - 1) / k;
for(; xx >= x; xx /= (k + 1));
} else {
y = (y - yy + k - 1) / k;
for(; yy >= y; yy /= (k + 1));
}
}
cout << x << "\n" ;
}
J A Game about Increasing Sequences 博弈
题意:
Alice,Bob在一个数组上玩游戏。
二人轮流取走头部或者尾部的一个数,每次取的数要严格大于之前取的全部的数。
无法取到的算输。
思路:
关键点, 找到一个必胜或者必败的局面
发现, 可以取的数来自于前缀上升,和后缀的下降
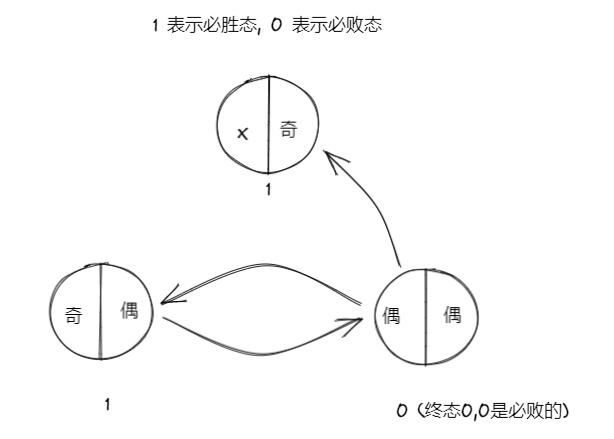
将可选两端分类, 把一端数字较大的叫 大端 , 一端数字较小的叫 小端
选了大端后, 那么小端就不能选了, 只能在大端选
状态转移
code
int n, L = 1, R = 1;
cin >> n;
fp(i, 1, n) {
cin >> a[i];
}
fp(i, 2, n) {
if(a[i] > a[i - 1]) L++;
else break;
}
fd(i, n - 1, 1) {
if(a[i] > a[i + 1]) R++;
else break;
}
if(L % 2 == 0 && R % 2 == 0) puts("Bob");
else puts("Alice");
B Non-decreasing Array dp暴力转移
题意
给定一个非递减数组a,每次操作:
可以选择一个数ai, 不能是开头或者结尾,
先删掉这个数, 然后在选一个数, 把它变成任意数
新数组必须满足非递减
依次输出1~n次操作后 ∑(ai−ai−1)2\sum {(a_{i} - a_{i - 1})^2}∑(ai−ai−1)2的最大值
思路
考虑3个点, 因为要满足非递减
所以, 如图:
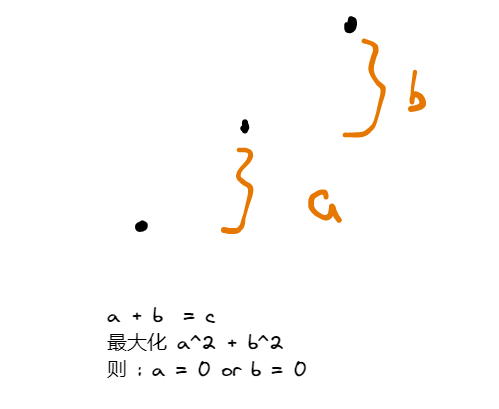
也就是, 变化一个点等价于删除一个点
k次操作可以删除 min(n - 2, 2 * k) 个数
n 只有100, 考虑暴力转移
状态定义: fi,j,k:=考虑到第i个数,上一个数是aj,已经删除了k个数f_{i, j , k} := 考虑到第i个数, 上一个数是a_j, 已经删除了k个数fi,j,k:=考虑到第i个数,上一个数是aj,已经删除了k个数
转移: fi,j,k:=max(fj,l,k′+cal(i,j)),k′=k−(i−j+1),1<=l<jf_{i,j,k} := max( f_{j,l,k'} + cal (i, j)), k' = k - (i - j + 1), 1<= l < jfi,j,k:=max(fj,l,k′+cal(i,j)),k′=





 本文介绍了2022年ICPC网络赛中涉及的算法和博弈问题,包括F Infinity Tree的规律寻找、A Game about Increasing Sequences的博弈策略、Non-decreasing Array的DP解决方案、Black and White Painting的模拟方法、以及Yet Another Remainder的费马小定理应用等。通过解析题目思路和提供代码示例,帮助读者理解这些问题的解决技巧。
本文介绍了2022年ICPC网络赛中涉及的算法和博弈问题,包括F Infinity Tree的规律寻找、A Game about Increasing Sequences的博弈策略、Non-decreasing Array的DP解决方案、Black and White Painting的模拟方法、以及Yet Another Remainder的费马小定理应用等。通过解析题目思路和提供代码示例,帮助读者理解这些问题的解决技巧。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








