Flip Game Poj1753

Flip Game

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 33621		Accepted: 14686

Description

Flip game is played on a rectangular 4x4 field with two-sided pieces placed on each of its 16 squares. One side of each piece is white and the other one is black and each piece is lying either it's black or white side up. Each round you flip 3 to 5 pieces, thus changing the color of their upper side from black to white and vice versa. The pieces to be flipped are chosen every round according to the following rules: 

1. Choose any one of the 16 pieces. 
   
2. Flip the chosen piece and also all adjacent pieces to the left, to the right, to the top, and to the bottom of the chosen piece (if there are any).

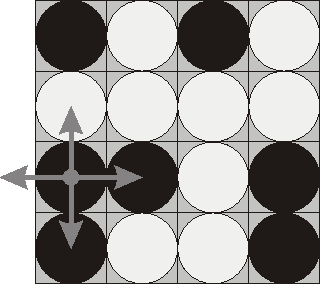Consider the following position as an example: 

bwbw 
wwww 
bbwb 
bwwb 
Here "b" denotes pieces lying their black side up and "w" denotes pieces lying their white side up. If we choose to flip the 1st piece from the 3rd row (this choice is shown at the picture), then the field will become: 

bwbw 
bwww 
wwwb 
wwwb 
The goal of the game is to flip either all pieces white side up or all pieces black side up. You are to write a program that will search for the minimum number of rounds needed to achieve this goal. 

Input

The input consists of 4 lines with 4 characters "w" or "b" each that denote game field position.

Output

Write to the output file a single integer number - the minimum number of rounds needed to achieve the goal of the game from the given position. If the goal is initially achieved, then write 0. If it's impossible to achieve the goal, then write the word "Impossible" (without quotes).

Sample Input

bwwb
bbwb
bwwb
bwww

Sample Output

4

 

 

和上道题目类似只不过不用标记并且对一维数组的转化方法也并不难。

 

 

#include <iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int map[20];
struct node
{
    int x,ans,a[20];
} q[100010];
void bfs()
{
    int i,j,k,s=0,e=0;
    node f1,f2;
    for(i=0; i<16; i++)
        f1.a[i]=map[i];
    f1.x=f1.ans=0;
    q[s++]=f1;
    while(s>e)
    {
        f1=q[e++];
        int ss=0;
        for(i=0;i<16;i++)
            ss+=f1.a[i];
        if(ss==0||ss==16)
        {
            cout<<f1.ans<<endl;
            return ;
        }
        for(i=0;i<16;i++)
        {
            f2=f1;
            if(f2.x<=i)
            {
                if( (i-4)>=0 )//上一行
                    f2.a[i-4]=1-f2.a[i-4];
                if( (i+4)<=15 )//下一行
                    f2.a[i+4]=1-f2.a[i+4];
                if( (i%4-1)>=0 )//左列
                    f2.a[i-1]=1-f2.a[i-1];//注意是下标是i-1而不是i%4-1;
                if( (i%4+1)<4 )
                    f2.a[i+1]=1-f2.a[i+1];
                f2.a[i]=1-f2.a[i];
                f2.x=i+1;
                f2.ans++;
                q[s++]=f2;
            }
        }
    }
    puts("Impossible");
    return ;
}
char s[4];
int main()
{
    int n,m,i,j,k;
    for(i=0; i<4; i++)
    {
        cin>>s;
        for(j=0; j<4; j++)
        {
            if(s[j]=='b')
            {
                map[i*4+j]=1;
            }
            else
                map[4*i+j ]=0;
        }
    }
    bfs();
    return 0;
}

 

过了一段时间再做这题结果TLE了，就是因为如果以某个旗子为中心的话，并且下面的若干次都以改旗子为中心，并翻转，会有重复的情况所以要，控制每个为中心的旗子只能翻一次。

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<queue>
#include<map>
#define L1 long long
#define L2 __int64
#define inf 0x3f3f3f3f

using namespace std;

const int m1=1001000;
const int m2=1010;
int head[m1],vex[m1],arr[m1],cnt;
bool vis[m2][m2];
char  s1[20],tm[10][10];

struct node
{
    int tmp,li;
    char s[20];
};

int bfs()
{
    int i;
    queue<node>q;
    while(!q.empty())
        q.pop();
    node f1,f2;

    for( i=0; i<16; i++)
        f1.s[i]=s1[i];
    f1.s[i]='\0';


    f1.li=f1.tmp=0;
    q.push(f1);

    while(!q.empty())
    {
        f1=q.front();
        q.pop();

        int bj=0;
        for(int i=1; i<16; i++)
        {
            if(f1.s[i]!=f1.s[i-1])
            {
                bj=1;
                break;
            }
        }
        if(!bj)
        {
            return f1.tmp;
        }

        for(int i=0; i<16; i++)
        {
            if(f1.li<=i)
            {
                f2=f1;
                f2.tmp++;
                if(f2.s[i]=='b')
                {
                    f2.s[i]='w';
                }
                else
                {
                    f2.s[i]='b';
                }
                if(i%4!=0)
                {
                    if(f2.s[i-1]=='b')
                    {
                        f2.s[i-1]='w';
                    }
                    else
                    {
                        f2.s[i-1]='b';
                    }
                }
                if(i>=4)
                {
                    if(f2.s[i-4]=='b' )
                    {
                        f2.s[i-4]='w';
                    }
                    else
                    {
                        f2.s[i-4]='b';
                    }
                }
                if( (i+1)%4!=0 )
                {
                    if(f2.s[i+1]=='b' )
                    {
                        f2.s[i+1]='w';
                    }
                    else
                    {
                        f2.s[i+1]='b';
                    }
                }
                if(i<12)
                {
                    if(f2.s[i+4]=='b')
                    {
                        f2.s[i+4]='w';
                    }
                    else
                    {
                        f2.s[i+4]='b';
                    }
                }
                f2.li=i+1;
                q.push(f2);
            }
        }
    }

    return inf;
}
int main()
{
    int n,m,i,j,k;
    for(i=0; i<4; i++)
        scanf("%s",tm[i]);
    for(i=0; i<4; i++)
        for(j=0; j<4; j++)
            s1[cnt++]=tm[i][j];
    s1[cnt]='\0';

    int p=bfs();
    if(p==inf)
    {
        printf("Impossible\n");
    }
    else
    {
        printf("%d\n",p);
    }
    return 0;
}