本文详细介绍了散列表的工作原理，包括哈希函数（如取余法和线性函数）、冲突处理（开放定址法与链地址法）以及STL中的散列函数和容器操作。通过实例演示了如何使用线性探测法避免散列冲突，并探讨了STL中的hashtable模板类及其插入操作。
一 哈希表的基本介绍:
散列表( Hash table,也叫哈希表)是根据关键码值(key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表。
那么他是如何映射的呢，就是通过哈希函数(散列函数)，常用的有取余法(h(x)= x mod p)，线性函数(h(x) = ax+b)，平方取中法(h(x = x*x的中间几位))。
好理解的取余法如下图。
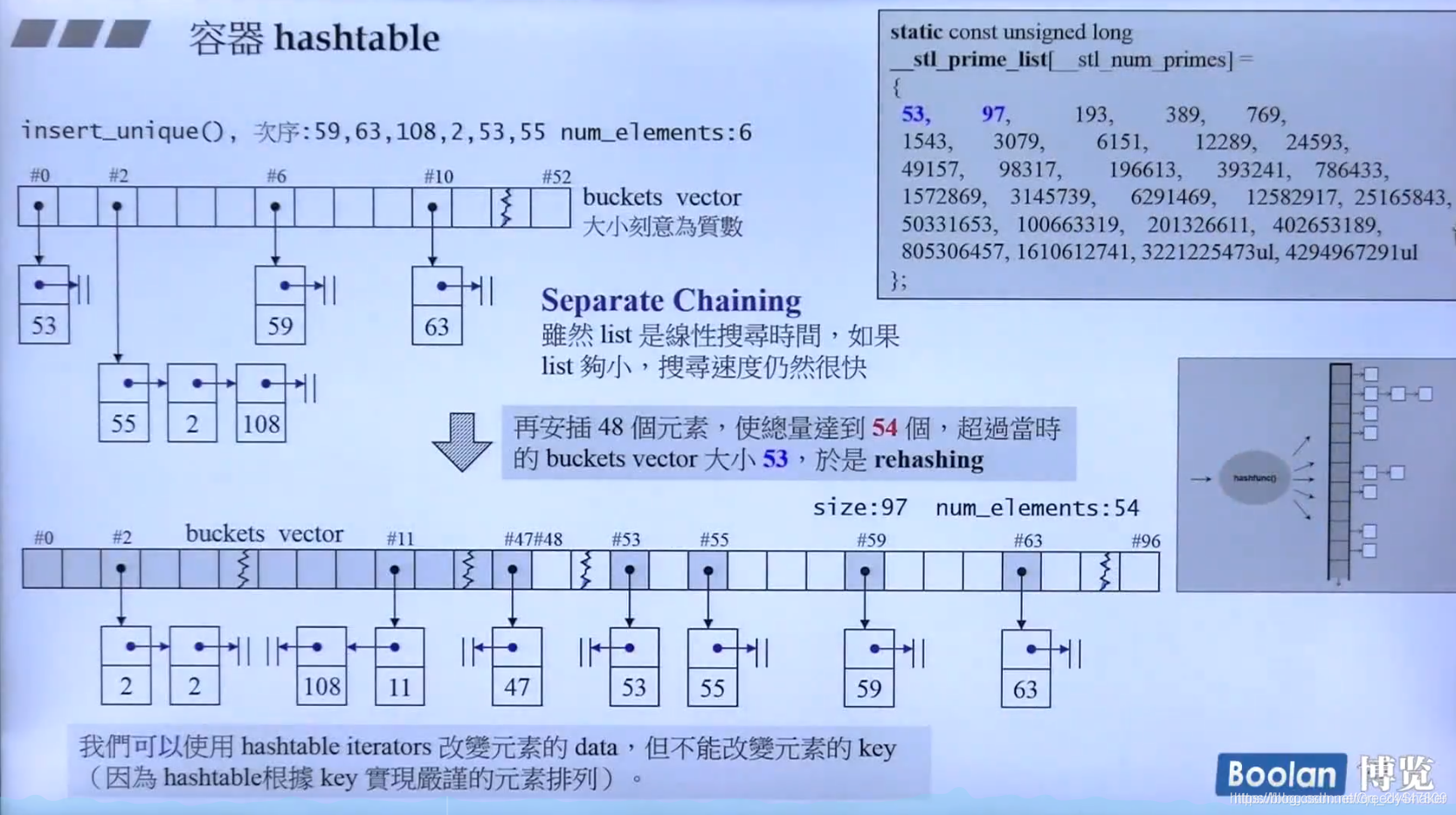
先看左上方的表，它以53取余，所以55，2，108都在2的下方。取余可以保证你的数据一定在这个区间内。右边是一个素数表，对素数取余保证你的散列分布相对均匀。下方的表是开链法，由于数据量巨大，比如上万个数据，那么这时对53取余就不太合适，这时就会对哈希表开链，重新生成一个新的哈希表。
散列冲突，就是上面的55，2，108对53取余都是2，那么这就是冲突了，对此我们有几种常用的方法，开放定址法（分为线性探测，二次探测（h’(x)= ((h(x)+ d）mod n) d是一组伪随机数），还有就是链地址法，就是2的后面其实是一个链表，那么其实就是对链表的操作了，添加，遍历，如上图。
三 小例子
首先输入一个整数，代表将要数。输入字符串的数量，然后输入字符串，将其存储起来
class MyHash
{
public:
MyHash()
{
fill(h,h+1542, 0);
}
int myhash(string str)
{
int r = 0;
for (int i = 0; i < str.size(); i++)
{
r = (r + 97 + str[i]) % 1543;
}
return r;
}
bool insert(string str)
{
int ha = myhash(str);
int h0 = ha;
h[ha];
while (s[h[ha]] != str)
{
if (h[ha] == 0)//当前位置没有被占用
{
h[ha] = cur;
s[cur] = str;
cur++;
return true;
}
ha = (ha + 97)%1543;//被占用，线性探测
if (ha == h0)//防止成环
{
ha = (h0 + 1) % 1543;
}
}
return false;
}
private:
int h[1542];
string s[10001];
int cur = 1;
};
int main()
{
MyHash myhash;
int c;
cin >> c;
int nCount = 0;
while (c--)
{
string str;
cin >> str;
if (myhash.insert(str))
nCount++;
}
cout << "count:" << nCount << endl;
return 0;
}
结果
这个例子，哈希函数采用线性函数，处理散列冲突采用开放定址法。还有一个find方法，觉得简单就没写，和插入是一样的，仔细想一下就明白
四 STL
stl的散列函数
可以发现数值类型的，hash函数的处理都是返回原值，但char*类型的进行单独处理，__stl_hash_string见下面
template <class Key> struct hash { };
/*字符串类型*/
inline size_t __stl_hash_string(const char* s)
{
/*处理方法*/
unsigned long h = 0;
for (; *s; ++s)
h = 5 * h + *s;
return size_t(h);
}
/*字符串类型，则调用上面处理方法*/
struct hash<char*>
{
size_t operator()(const char* s) const { return __stl_hash_string(s); }
};
struct hash<const char*>
{
size_t operator()(const char* s) const { return __stl_hash_string(s); }
};
/*下面各种类型直接返回，无需额外处理*/
struct hash<char> {
size_t operator()(char x) const { return x; }
};
struct hash<unsigned char> {
size_t operator()(unsigned char x) const { return x; }
};
struct hash<signed char> {
size_t operator()(unsigned char x) const { return x; }
};
struct hash<short> {
size_t operator()(short x) const { return x; }
};
struct hash<unsigned short> {
size_t operator()(unsigned short x) const { return x; }
};
struct hash<int> {
size_t operator()(int x) const { return x; }
};
struct hash<unsigned int> {
size_t operator()(unsigned int x) const { return x; }
};
struct hash<long> {
size_t operator()(long x) const { return x; }
};
struct hash<unsigned long> {
size_t operator()(unsigned long x) const { return x; }
};
//面这些包装函数最终会调用 hash(key) % n ，hash函数取编号，
//之后再对n取余后自然可以找到自己该放在哪个buckets
size_type bkt_num_key(const key_type& key) const
{
return bkt_num_key(key, buckets.size());
}
size_type bkt_num(const value_type& obj) const
{
return bkt_num_key(get_key(obj));
}
size_type bkt_num_key(const key_type& key, size_t n) const
{
return hash(key) % n;
}
size_type bkt_num(const value_type& obj, size_t n) const
{
return bkt_num_key(get_key(obj), n);
}
插入操作与表格重整
/*以下函数判断是否需要重建表格。如果不需要，立即返回。如果需要，就重建*/
template <class V, class K, class HF, class Ex, class Eq, class A>
void hashtable<V, K, HF, Ex, Eq, A>::resize(size_type num_elements_hint)
{
const size_type old_n = buckets.size();//bucket vector 的大小
/*如果元素个数(把新增元素计入后)比bucket vector 大，则需要重建表格*/
if (num_elements_hint > old_n) {
const size_type n = next_size(num_elements_hint);//找出下一个质数
if (n > old_n) { //old_n不是质数表里面的最大值时，才可扩展
vector<node*, A> tmp(n, (node*)0);//设立新的bucket vector，大小为n
try {
//以下处理每一个旧的bucket
for (size_type bucket = 0; bucket < old_n; ++bucket) {
node* first = buckets[bucket];//指向节点所对应之串行(链表)的起始节点
while (first) {//处理单个bucket中的链表
size_type new_bucket = bkt_num(first->val, n);//找出节点落在哪一个新的bucket内
buckets[bucket] = first->next;//令旧bucket指向其所对应的链表的下一个节点，以便迭代处理
/*下面将当前节点插入到新的bucket内，成为其对应链表的第一个节点，这里的实现比较巧妙
相当于插入新节点到新bucket vector中，新插入的元素插入到链表的首位置，这里不同于一般的插入的是，
由于之前已有元素占据空间，这里只是修改节点指针指向*/
first->next = tmp[new_bucket];
tmp[new_bucket] = first;
first = buckets[bucket];//回到旧bucket所指的待处理链表，准备处理下一个节点
//first = old_first->next;
}
}
buckets.swap(tmp);//vector::swap 新旧两个buckets 对调（浅修改）
/*对调两方如果大小不同，大的会变小，小的会变大，离开时释放local tmp 的内存*/
}
catch (...) {
for (size_type bucket = 0; bucket < tmp.size(); ++bucket) {
while (tmp[bucket]) {
node* next = tmp[bucket]->next;
delete_node(tmp[bucket]);
tmp[bucket] = next;
}
}
throw;
}
}
}
}
/*插入元素，不允许重复*/
template <class V, class K, class HF, class Ex, class Eq, class A>
pair<hashtable<V, K, HF, Ex, Eq, A>::iterator, bool>
hashtable<V, K, HF, Ex, Eq, A>::insert_unique_noresize(const value_type& obj)
{
const size_type n = bkt_num(obj);//定位bucket
node* first = buckets[n];
/*判断插入元素是否有重复*/
for (node* cur = first; cur; cur = cur->next)
if (equals(get_key(cur->val), get_key(obj)))
return pair<iterator, bool>(iterator(cur, this), false);
node* tmp = new_node(obj);//产生新节点 node_allocator::allocate()
/*先插入节点放在链表最前面*/
tmp->next = first;
buckets[n] = tmp;
++num_elements;//元素个数增加
return pair<iterator, bool>(iterator(tmp, this), true);
}
/*插入元素，允许重复*/
template <class V, class K, class HF, class Ex, class Eq, class A>
hashtable<V, K, HF, Ex, Eq, A>::iterator
hashtable<V, K, HF, Ex, Eq, A>::insert_equal_noresize(const value_type& obj)
{
const size_type n = bkt_num(obj);//定位bucket
node* first = buckets[n];//链表头节点
for (node* cur = first; cur; cur = cur->next)
if (equals(get_key(cur->val), get_key(obj))) {//如果插入元素是重复的(与cur->val重复)
node* tmp = new_node(obj);
tmp->next = cur->next;//新增元素插入重复元素的后面
cur->next = tmp;
++num_elements;
return iterator(tmp, this);
}
//没有重复，等同于insert_unique_noresize()
node* tmp = new_node(obj);
tmp->next = first;
buckets[n] = tmp;
++num_elements;
return iterator(tmp, this);
}
扫一扫
1801
到【灌水乐园】发言
