Leetcode 200. Number of Islands

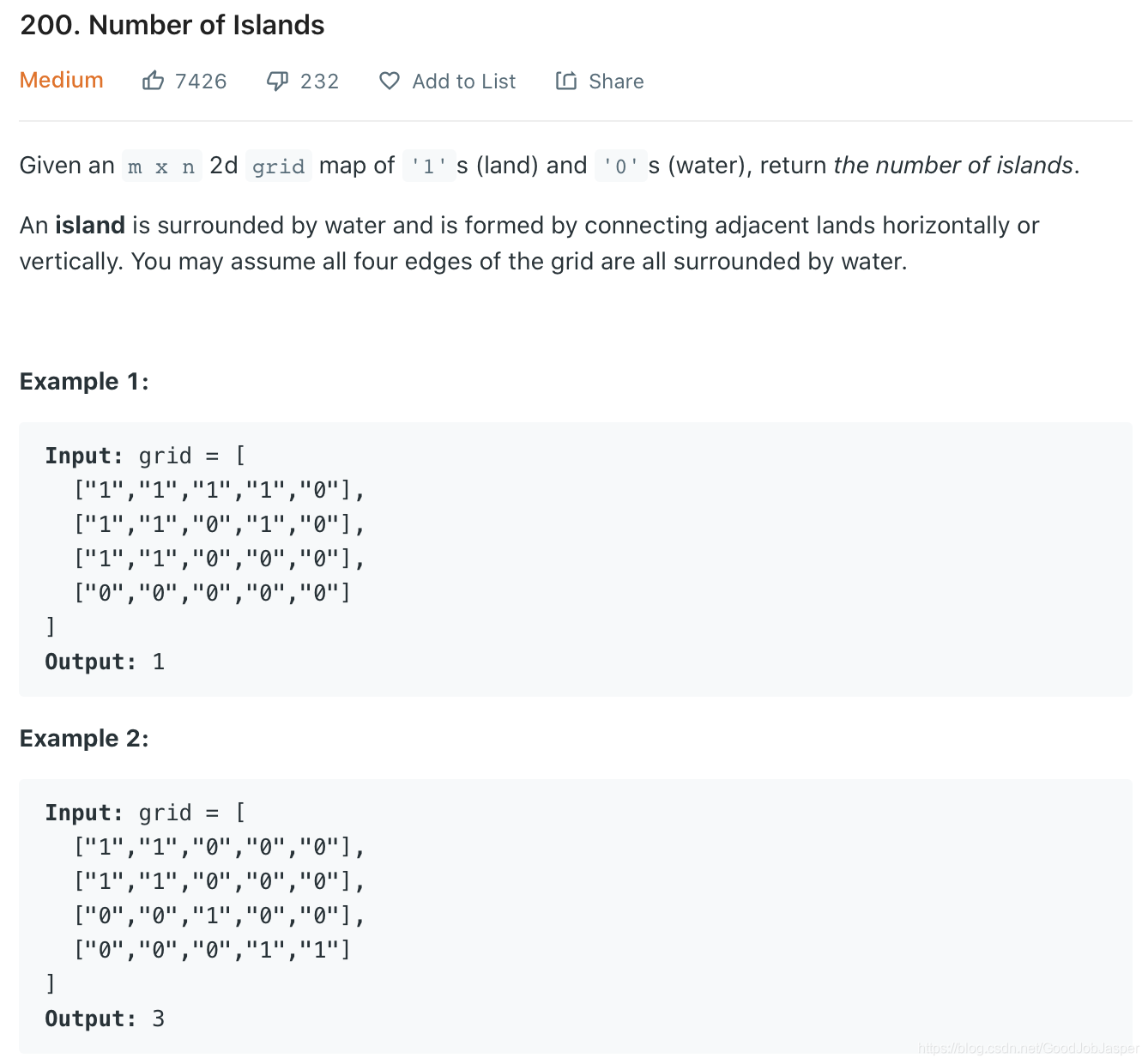
方法1: dfs/backtracking。这道题我不知道为啥没能想出来咋做，因为我感觉不是很难，可能是在看完答案之后觉得不是很难吧。直接上代码，时间复杂mn，空间复杂worst case mn

class Solution {
    int m;
    int n;
    public int numIslands(char[][] grid) {
        int count = 0;
        m = grid.length;
        if(m == 0) return 0;
        n = grid[0].length;
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(grid[i][j] == '1'){
                    dfs(grid, i, j);
                    count++;
                }
            }
        }
        return count;
    }
    
    public void dfs(char[][] grid, int i, int j){
        if(i < 0 || j < 0 || i >= m || j >= n || grid[i][j] != '1') return;
        grid[i][j] = '0';
        dfs(grid, i - 1, j);
        dfs(grid, i + 1, j);
        dfs(grid, i, j - 1);
        dfs(grid, i, j + 1);
    }
}

方法2: bfs-one queue。时间复杂m*n，空间复杂worst case Min(m,n)。bfs空间复杂分析如下图：

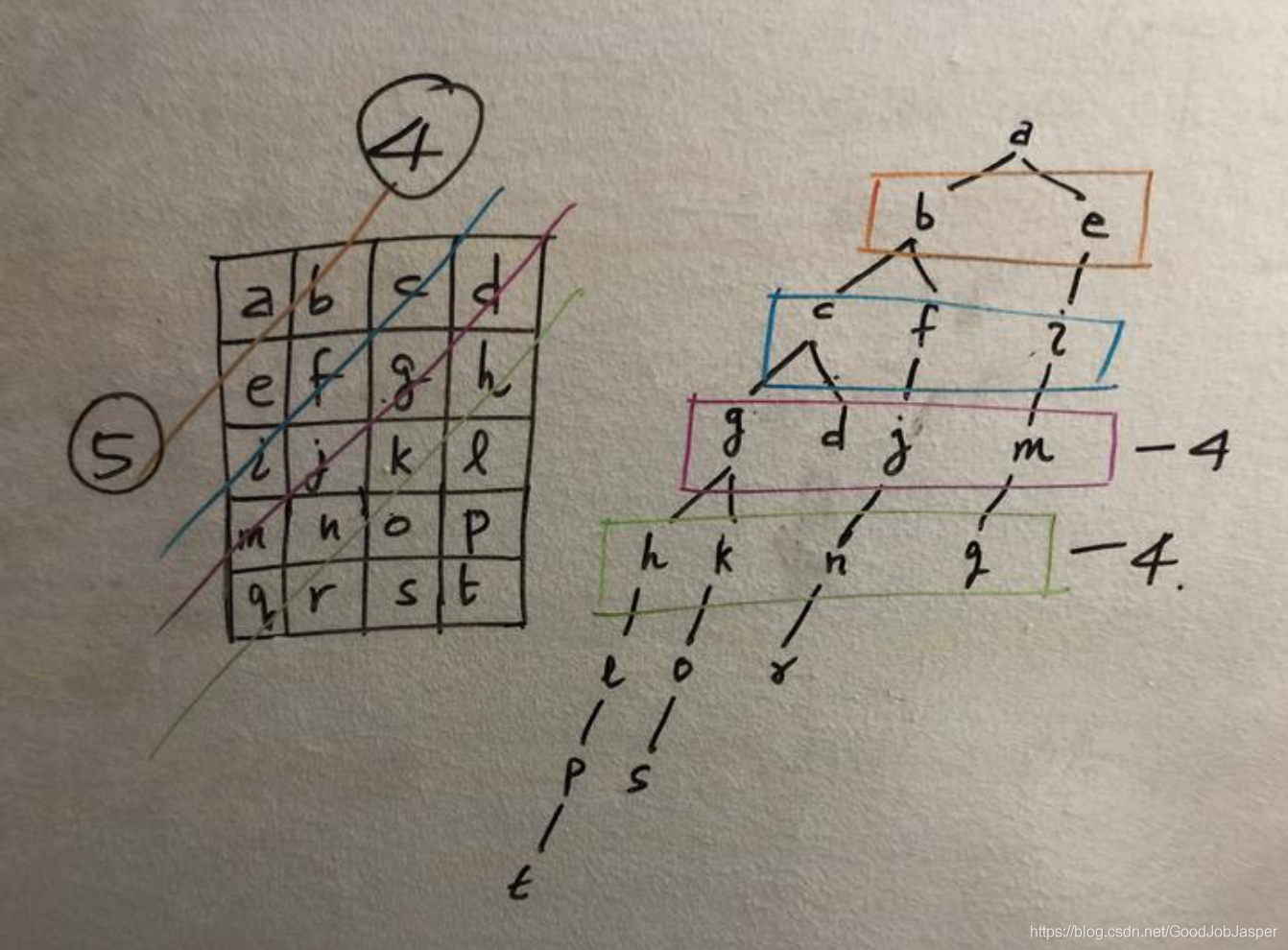
总结：

• 这道题复盘的时候要再仔细思考dfs与bfs有什么区别。我目前觉得区别是在于把‘1’node标为0的顺序不同。一个是纵向的一个是横向的。