问题描述:
- 设计一棋盘覆盖问题算法(分治法)
- 并计算其时间复杂度(要求写出递推公式,及其求解过程)
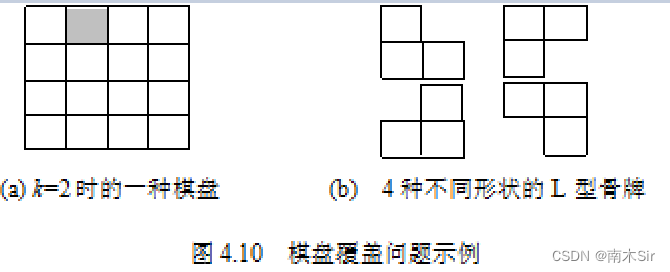
在一个2k×2k 个方格组成的棋盘中,恰有一个方格与其它方格不同,称该方格为一特殊方格,且称该棋盘为一特殊棋盘。在棋盘覆盖问题中,要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格,且任何2个L型骨牌不得重叠覆盖。
(该算法中可能用到的变量: tr :棋盘中左上角方格所在行;tc :棋盘中左上角方格所在列。 dr: 残缺方块所在行;dl
:残缺方块所在列。 size:棋盘的行数或列数;用二维数组board[ ][ ],模拟棋盘。)
分治的技巧在于如何划分棋盘,使划分后的子棋盘的大小相同,并且每个子棋盘均包含一个特殊方格,从而将原问题分解为规模较小的棋盘覆盖问题。
k>0时,可将2k×2k的棋盘划分为4个2(k-1)×2(k-1)的子棋盘。这样划分后,由于原棋盘只有一个特殊方格,所以,这4个子棋盘中只有一个子棋盘包含该特殊方格,其余3个子棋盘中没有特殊方格。
为了将这3个没有特殊方格的子棋盘转化为特殊棋盘,以便采用递归方法求解,可以用一个L型骨牌覆盖这3个较小棋盘的会合处,从而将原问题转化为4个较小规模的棋盘覆盖问题。
递归地使用这种划分策略,直至将棋盘分割为1×1的子棋盘。
代码如下:
def chess(tr,tc,pr,pc,size):
global mark
global table
if size==1:
return #递归终止条件
mark+=1 #表示直角骨牌号
count=mark
half=size//2 #当size不等于1时,棋盘格规模减半,变为4个
#小棋盘格进行递归操作
#左上角
if (pr<tr+half) and (pc<tc+half):
chess(tr,tc,pr,pc,half)
else:
table[tr+half-1][tc+half-1]=count
chess(tr,tc,tr+half-1,tc+half-1,half)
#将[tr+half-1,tc+half-1]作为小规模棋盘格的特殊点,进行递归
#右上角
if (pr<tr+half) and (pc>=tc+half):
chess(tr,tc+half,pr,pc,half)
else:
table[tr+half-1][tc+half]=count
chess(tr,tc+half,tr+half-1,tc+half,half)
#将[tr+half-1,tc+half]作为小规模棋盘格的特殊点,进行递归
#左下角
if (pr>=tr+half) and (pc<tc+half):
chess(tr+half,tc,pr,pc,half)
else:
table[tr+half][tc+half-1]=count
chess(tr+half,tc,tr+half,tc+half-1,half)
#将[tr+half,tc+half-1]作为小规模棋盘格的特殊点,进行递归
#右下角
if (pr>=tr+half) and (pc>=tc+half):
chess(tr+half,tc+half,pr,pc,half)
else:
table[tr+half][tc+half]=count
chess(tr+half,tc+half,tr+half,tc+half,half)
#将[tr+half,tc+half]作为小规模棋盘格的特殊点,进行递归
def show(table):
n=len(table)
for i in range(n):
for j in range(n):
print(table[i][j],end=' ')
print('')
if __name__=='__main__':
mark = 0
k = 8
table=[[-1 for x in range(k)] for y in range(k)] #-1代表特殊格子
chess(0,0,2,2,k)
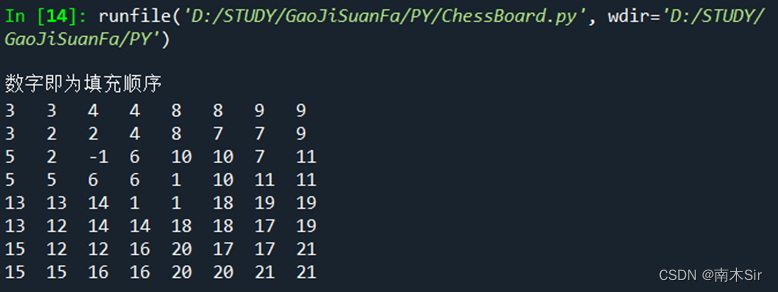
print('\n数字即为填充顺序')
show(table)
递推公式:



























 1015
1015

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










