出现incompatible types: possible lossy conversion from double to int错误

最新推荐文章于 2022-11-16 17:44:43 发布

原创最新推荐文章于 2022-11-16 17:44:43 发布 · 7.3k 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#动态规划 #算法 #java #c++

解决方案专栏收录该内容

11 篇文章

订阅专栏

力扣357题求解过程中遇到类型转换问题，当涉及Math.pow运算时，结果为double类型导致与int类型不兼容。通过在运算中加入(int)强转解决此错误。同时提供了问题的动态规划解决方案和C++版本的代码实现。

【力扣357题】计算各个位数不同的数字个数原题链接：力扣

给定一个非负整数 n，计算各位数字都不同的数字 x 的个数，其中 0 ≤ x < 10^n 。

输入: 2
输出: 91 
解释: 答案应为除去 11,22,33,44,55,66,77,88,99 外，在 [0,100) 区间内的所有数字。

思路：动态规划

class Solution {
    public int countNumbersWithUniqueDigits(int n) {
        int[] dp = new int[n + 1];
        for(int i = 2; i <= n; i++) {
            dp[i] = dp[i - 1] * 10 + (9 * Math.pow(10, i -2) - dp[i - 1]) * (i - 1);
        }
        int sum = 0;
        for(int num : dp) {
            sum += num;
        }
        return Math.pow(10, n) - sum;
    }
}

出错：

这里发生了不兼容类型错误：从double到int可能出现有损转换

分析：

定义dp数组时是int类型，但是在 (9 * Math.pow(10, i -2) - dp[i - 1]) * (i - 1)

以及Math.pow(10, n) - sum出现为double类型

因为Math.pow()方法返回值是double类型

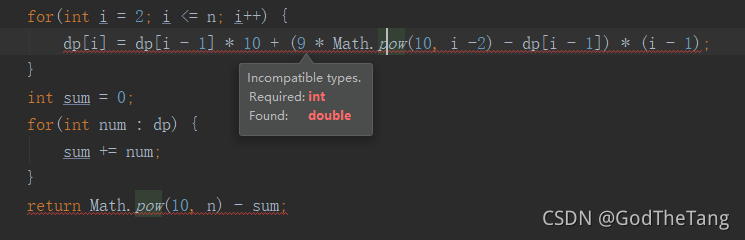
解决：在这里加（int）强转一下即可

class Solution {
    public int countNumbersWithUniqueDigits(int n) {
        int[] dp = new int[n + 1];
        for(int i = 2; i <= n; i++) {
            dp[i] = dp[i - 1] * 10 + (int)(9 * Math.pow(10, i -2) - dp[i - 1]) * (i - 1);
        }
        int sum = 0;
        for(int num : dp) {
            sum += num;
        }
        return (int)Math.pow(10, n) - sum;
    }
}

附带C++版本

class Solution {
public:
    int countNumbersWithUniqueDigits(int n) {
        vector<int> dp(n+1);
        for(int i = 2; i <= n; ++i)
            dp[i] = dp[i-1]*10 + (9*pow(10, i-2) - dp[i-1])*(i-1);
        int sum = 0;
        for(auto& x : dp)
            sum += x;
        return pow(10, n) - sum;
    }
};