整理低秩的理解

秩的定义是矩阵中非零特征值的个数。比如一个NxN的矩阵，它的秩为r，r远小于N，我们可以说它是低秩的。

但还有另一种情况：这个矩阵的的秩接近N，但它的特征值大多数接近于0，只有少数几个特征值特别大，这种也可以认为是低秩的。

如果我们将低秩图像的特征值从大到小排列，会得到这样一条曲线：

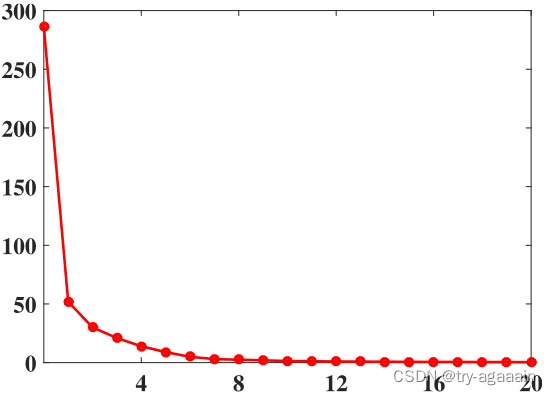
（纵坐标为特征值的大小，横坐标为不同的特征值下标）

从特征向量的角度来理解低秩的含义：矩阵只需要极少数的几个特征向量就能近似还原出原先矩阵中的每个向量。

在用这些特征向量还原矩阵的过程中，不同特征向量起到的作用是有差异的，特征值越大的特征向量，它和矩阵中的大部分向量越相似，所以只需要用前几个重要特征向量进行线性组合，就能近似的还原矩阵中的大多数向量。

如果我们将低秩矩阵X分解为A*Z，可以将A看作是特征向量，或者说是基向量组（基底），Z为图像的系数表示矩阵。那么可以取前r个特征向量$A^{\prime }=A\in R^{N\times r}$和对应的系数矩阵$Z^{\prime }=Z\in R^{r\times N}$相乘，得到$X^{\prime }=A^{\prime }\ast Z^{\prime }$的和原矩阵X是很接近的。

下面选用了一张有较多重复图案的图像，这类图像由于图像细节的相似性往往具有低秩特点，在RGB三通道上进行依次选用前k个特征向量来还原原图：

可以看到，仅使用一个特征向量便能大致刻画图像的图案特征，当选用前20个特征向量时，基本能很好的还原出原始图像的细节了。

在刚接触PCA时，常将其用于数据压缩，比如一个多分类问题，每条样本包含大量的属性，而有些属性并不关键，去掉这些属性对分类影响不大，于是通过PCA将原先由N个属性表示的样本压缩为r（r<<N）个属性表示，使数据的处理更加方便。在这个过程中，剩下的信息也是用少数r个特征向量来表示的，它们对应的特征值都较大。

我们会用能量来表示特征向量的作用，它计算很简单，第i个特征向量的能量为：该特征值 / 所有特征值之和。对于低秩矩阵来说，用能量占比前90%的前几个特征就能表示出原矩阵了，恢复的误差很小。

即使是一般的图像，也常常会用类似的方式压缩信息，以便节省传输过程中的流量，有时候我们会看到一些高糊的表情包，可能就是不断压缩的结果（趣称为“电子包浆”）。

在包含上百个波段的高光谱图像中，各个波段的图像很相似，因而往往具有低秩性。很多方法会根据这种性质对高光谱图像进行恢复。