如何利用分治法解决最大子段和问题

最新推荐文章于 2022-05-29 10:34:52 发布

原创

最新推荐文章于 2022-05-29 10:34:52 发布 · 1.1k 阅读

5 ·

CC 4.0 BY-SA版权

文章标签：

#算法

本文介绍了最大子段和问题，即在数组中寻找连续子序列的元素和最大值。通过阐述分治法的基本思想和策略，文章探讨了如何应用分治法来解决这个问题，并给出了具体的分治法实现代码。最后，总结了不同解法的时间复杂度，包括分治法的O(nlogn)复杂度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

什么是最大子段和问题？

在一个数组或者序列当中，有n个数，我们需要找出一段非空的连续区间，使得这个区间内所有元素之和最大。

什么是分治法？

分治法的基本思想：将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。

分治策略：对于一个规模为n的问题，若该问题可以容易的解决(比如规模n较小)则直接解决，否则将其分解为k个规模较小的子问题，这些子问题互相独立且与原问题形式相同，递归地解决这些子问题，然后将各个子问题的解合并得到原问题的解。

怎么引入分治法的思想呢？

我们想在这个数组中找到一段元素之和最大的区间，那么把这段数组一分为二，在两个子数组中各找到一段元素之和最大的区间，此时可能会出现整个数组中最大的元素之和的区域呢分三个，左边区域，右边区域，穿过左右区域的新区域。

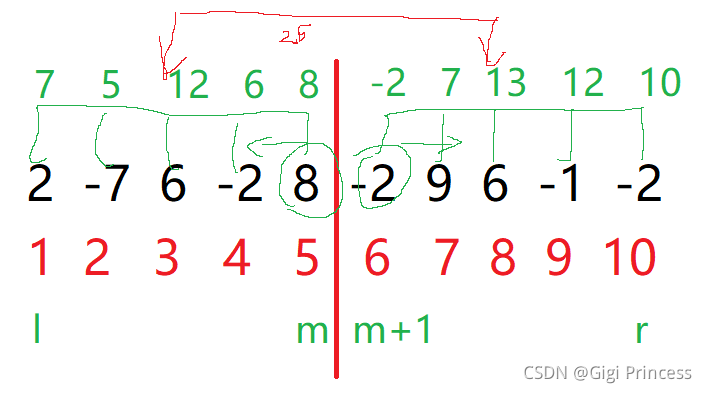
实现代码：

#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include <algorithm>
using namespace std;

const int N = 100000 + 5;
int n = 10, a[N] = { 2, -7, 6, -2, 8, -2, 9, 6, -1, -2 };
int f(int l, int r)
{
	//a[l]....a[r]横跨左右的最大最大子段和
	int m = (l + r) / 2;//中点
	int sumL = 0, ansL = a[m];//中点左侧 一个是和，一个是想要的最大值
	int sumR = 0, ansR = a[m + 1];//中点右侧 一个是和，一个是想要的最大值