链表相交之谜：一招“路径对齐”搞定！-优快云博客

你好，算法爱好者！

今天，我们来破解一个经典的链表面试题：。寻找两个链表的第一个相交节点

你可能会想：这不简单，用哈希表记录一个链表的所有节点，再遍历另一个链表不就行了？可以，但这需要 O(N) 的额外空间。或者，先计算两个链表的长度差，让长链表的指针先走 dd 步，然后两个指针再一起走？也可以，但这需要遍历两次。

有没有一种方法，只用 O(1) 的空间，并且逻辑上只遍历一次就能解决问题？答案是肯定的，而且它的思路美妙得像一首诗。

一、问题的核心：不等长的“赛道”

想象一下，两个指针和p1p2 分别是两条链表和 AB 上的赛跑选手。我们的目标是让他们在相遇。第一个交叉路口 c1

最大的障碍是：。如果他们同时出发，同速前进，在到达交叉口之前，他们走过的路程不同，因此无法同时到达。两条赛道（链表）的长度可能不同

      a1 -> a2
              \
               c1 -> c2 -> c3
              /
b1 -> b2 -> b3

如上图，从 p1a1 出发，从 p2b1 出发，显然的路程更长，他们无法在 p2c1 相遇。

二、天才般的构想：让赛道“逻辑上”等长 (★★★★★)

重要性评级： ★★★★★ (核心思想，极度巧妙，面试必考)
一句话解释： 我走完我的路再走一遍你的路，你走完你的路再走一遍我的路，我们走的总路程就一样了！

这个想法的数学原理是：。len(A) + len(B) = len(B) + len(A)

我们让两个指针和p1p2 这样跑：

p1：先遍历链表，到达终点 ANone 后，到链表 瞬间转移B 的头部，继续遍历。
p2：先遍历链表，到达终点 BNone 后，到链表 瞬间转移A 的头部，继续遍历。

为什么这样可行？

p1 走过的总路程 = len(A) + len(B)
p2 走过的总路程 = len(B) + len(A)

他们的总路程完全相同！这意味着，如果存在一个交点，他们最终必将在这个交点相遇。

图解这个“伟大的旅程”：

p1 的旅程:
的旅程: a1 -> a2 -> c1 -> c2 -> c3 -> (跳转) -> b1 -> b2 -> b3 -> c1 -> ...p2b1 -> b2 -> b3 -> c1 -> c2 -> c3 -> (跳转) -> a1 -> a2 -> c1 -> ...

可以清晰地看到，在他们各自完成第一段旅程并“交换赛道”后，他们都会在这个节点上相遇！c1

三、代码实现：优雅的极致 (★★★★☆)

重要性评级： ★★★★☆ (代码极简，但蕴含深意，需要能徒手写出并解释)

这个天才般的构想，其代码实现却短得令人惊叹。

生成的 python

      class Solution:
    def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
        if not headA or not headB:
            return None

        p1, p2 = headA, headB

        while p1 != p2:
            # p1 走一步，如果到达末尾，则切换到 headB
            p1 = p1.next if p1 else headB
            
            # p2 走一步，如果到达末尾，则切换到 headA
            p2 = p2.next if p2 else headA
            
        # 循环结束时，p1 和 p2 要么在交点相遇，要么都为 None
        return p1

代码剖析：p1 = p1.next if p1 else headB
这行代码是 Python 的三元表达式，等价于：

生成的 python

      if p1 is not None:
    p1 = p1.next  # 如果 p1 没到头，就正常走一步
else:
    p1 = headB    # 如果 p1 走到了 A 的尽头 (None)，就跳到 B 的开头

这正是我们“交换赛道”逻辑的完美实现。

四、灵魂拷问：如果没有交点呢？

你可能会问：如果两个链表平行，永不相交，这个代码会死循环吗？

答案是：不会，它会优雅地结束并返回 None。

指针移动过程模拟：

假设链表 A 的长度为 m，链表 B 的长度为 n：

指针 p1 的路径：
- 从 A 的头节点出发，走 m 步到达 A 的末尾（指向None）。
- 跳到 B 的头节点，再走 n 步到达 B 的末尾，最终指向 None。
- 总步数：m + n。
指针 p2 的路径：
- 从 B 的头节点出发，走 n 步到达 B 的末尾（指向None）。
- 跳到 A 的头节点，再走 m 步到达 A 的末尾，最终指向 None。
- 总步数：n + m。
循环终止条件：
当 p1 和 p2 都指向None时，while p1 != p2的条件为False（因为None == None），循环结束，返回None。

五、随堂测验（检验你的掌握程度）

问题 1：在这个算法中，两个指针 p1 和 p2 最多会走多少步？（假设链表 A 的独立部分长 a，链表 B 的独立部分长 b，公共部分长 c）

答案：最多 a + b + c 步。

详细解析：

有交点的情况：
- 若交点在公共部分，p1 走过的距离为 a + c，p2 走过的距离为 b + c。
- 当 a = b 时，两者直接在交点相遇；若 a ≠ b，则指针会 “交换赛道” 后继续移动，直到总路程相等（a + c + b = b + c + a），最终在交点相遇。
- 总步数：不超过 a + b + c。
无交点的情况：
- 此时公共部分长度 c = 0，链表 A 和 B 的总长度分别为 a 和 b。
- p1 和 p2 会走完两条链表的总长度（a + b），最终同时指向None，总步数为 a + b，仍满足 a + b + c（因为c=0）。
本质逻辑：
算法通过 “交换赛道” 确保两个指针的总路程相等（均为 len(A) + len(B)），因此无论是否有交点，指针最多走 (a + c) + (b) = a + b + c 步（或 (b + c) + (a) = a + b + c 步）。

问题 2：如果其中一个链表是空的，比如 headA 是 None，函数 getIntersectionNode 会如何表现？

答案：函数会正确返回 None。

两种情况解析：

有初始判断的情况：
代码中通常会有初始判断 if not headA or not headB: return None，直接处理空链表情况，返回None。
无初始判断的情况：
- 假设 headA 为None，p1 初始化为None，p2 初始化为headB。
- 第一次循环：p1 变为headB，p2 变为headB.next。
- 后续循环：p1 沿 B 链表移动，p2 沿 B 链表移动，直到两者都指向None。
- 最终p1 == p2 == None，循环结束，返回None。

问题 3：这个 “交换赛道” 的技巧，和 “快慢指针” 有什么本质区别？

答案：两者的解决模型和核心思想完全不同。

这个技巧不仅代码优美，思想更是深刻，希望你已经领会到了它的魅力！

如何求两个链表的相交节点呢

以下是借鉴Github上labuladong大佬的算法图片

图中C1就是两链表的交点

由于两条链表的长度可能不同，两条链表之间的节点无法对应：

如果两个指针p1和p2分别在链表上前进的话就不能够同时走到公共节点，解决这个问题的关键就是通过某些方式让其能够同时到达相交节点c1

所以，我们可以让 p1 遍历完链表 A 之后开始遍历链表 B，让 p2 遍历完链表 B 之后开始遍历链表 A，这样相当于「逻辑上」两条链表接在了一起。

如果这样进行拼接，就可以让 p1 和 p2 同时进入公共部分，也就是同时到达相交节点 c1：

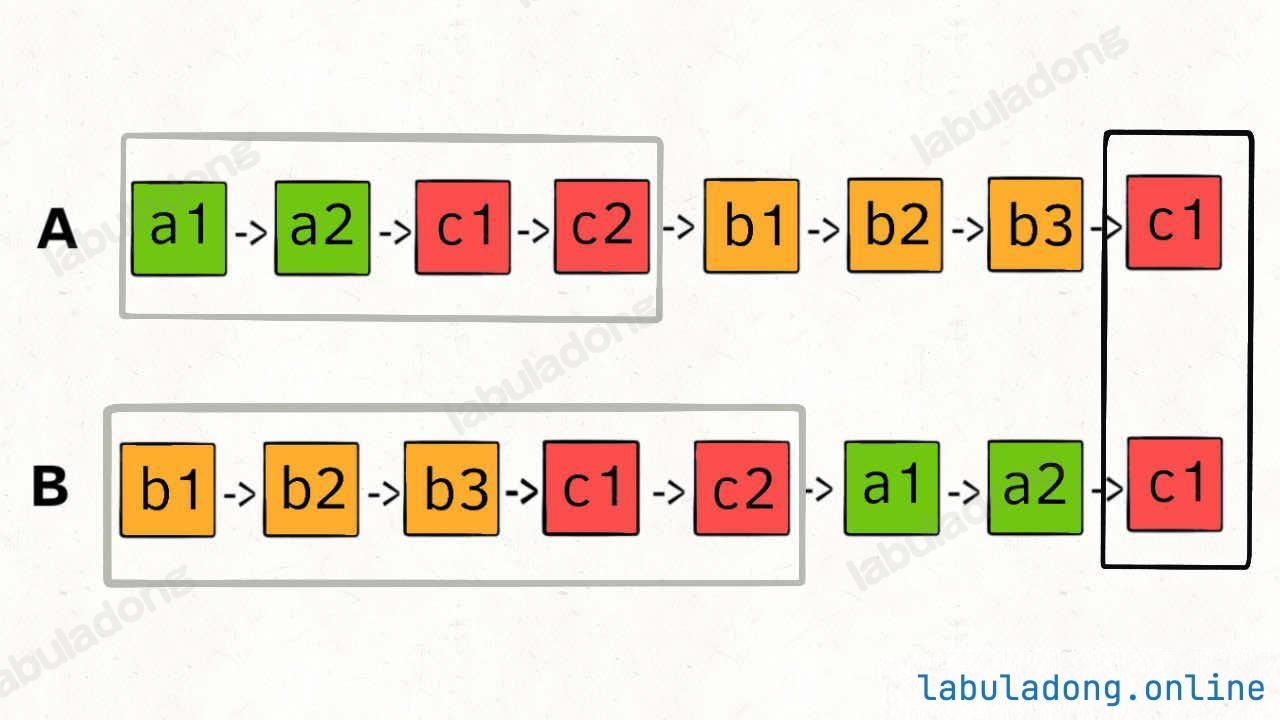
那你可能会问，如果说两个链表没有相交点，是否能够正确的返回 null 呢？

这个逻辑可以覆盖这种情况的，相当于 c1 节点是 null 空指针嘛，可以正确返回 null。

按照这个思路，可以写出如下代码：

class Solution:
    def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
        # p1 指向 A 链表头结点，p2 指向 B 链表头结点
        p1, p2 = headA, headB
        while p1 != p2:
            # p1 走一步，如果走到 A 链表末尾，转到 B 链表
            p1 = p1.next if p1 else headB
            # p2 走一步，如果走到 B 链表末尾，转到 A 链表
            p2 = p2.next if p2 else headA
        return p1