Dijkstra算法求解无向图一点到其他各点的最短路径

原创

已于 2022-08-08 09:39:26 修改 · 1.9k 阅读

19 ·

CC 4.0 BY-SA版权

文章标签：

#dijkstra #算法 #c++

于 2021-06-18 21:20:31 首次发布

本文介绍了一个使用Dijkstra算法求解无向带权图中顶点V1到其他各顶点最短路径的问题。通过邻接矩阵表示图结构，并采用C++实现算法流程，最终展示从指定起点到各个顶点的最短路径及其距离。

Dijkstra求解最短路径

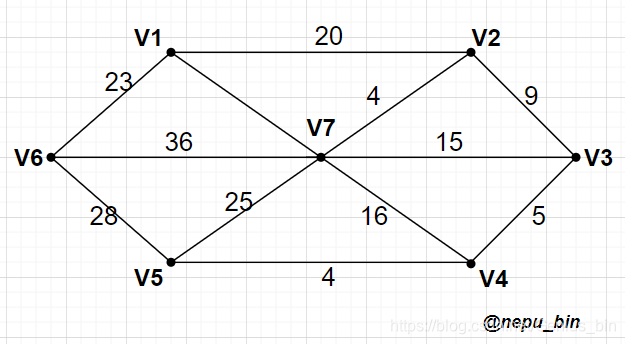
在这里插入图片描述
有一无向带权图，求解顶点V1到其他各顶点的最短路径。

实现代码

#include <iostream>
#include <vector>
#include <unordered_set>
using namespace std;

struct edge {
   
   
	int start;//起点
	int end;//终点
	int distance;//距离 (边权)
	edge(int s, int e, int d) :start(s), end(e), distance(d) {
   
   }
};

void init(vector<edge>& edges, vector<vector<int>>& inf);
void Dijkstra(vector<vector<int>>& inf, int fir, int& n);
void findPath(vector<pair<int, int>> path, vector<vector<int>>& inf, int fir, int& n);
//初始化邻接矩阵
void init(vector<edge>& edges, vector<vector<int>>& inf) {
   
   
	edges.push_back(edge(0, 1, 20));
	edges.push_back(edge(1, 2, 9));
	edges.push_back(edge(2, 3, 5));
	edges.push_back(edge(3, 4, 4));
	edges.push_back(edge(4, 5, 28));
	edges.push_back(edge(5, 0, 23));
	edges.push_back(edge(6, 0, 1));
	edges.push_back(edge(6, 1, 4));
	edges.push_back(edge(6, 2, 15));
	edges.push_back(edge(6, 3, 16));
	edges.push_back(edge(6, 4