位和位运算（32位和64位）

位

CPU位数

1. 寄存器：存放数值，大小叫位宽。32位CPU能放入最大2^32 的数值，
   64位就是最大2^64的值。32位位宽的CPU就是常说的32位CPU，同理64位CPU也是一样。

2. 总线：CPU跟内存之间，是用总线来进行信号传输的，总线可以分为数据总线，控制总线，地址总线。
   32位CPU的总线宽度一般是32位，最大能寻址的范围，也就到2^32，就是4G。
   64位CPU，按理说总线宽度是64位，但实际上是48位，所以寻址范围能到2^48次方，也就是256T。

系统和软件的位数

1. 在操作系统上运行一个用户态进程，会分为用户态和内核态，并设定一定的内存布局。
2. 操作系统和软件都需要以这个内存布局为基础运行程序。32位机器，内核态分配了1个G，用户态分配了3G，总不能将程序的运行内存边界设定在大于10G的地方。所以，系统和软件的位数，可以理解为，这个系统或软件内存寻址的范围位数。
   

程序的执行

代码，最后会变成一堆01机器码，放在可执行文件里，躺在磁盘上

1. 文件：硬盘->内存->CPU

2. CPU：

   1. 内存数据->总线->寄存器
   2. 寄存器->总线->内存

进制

任何一种进位计数制都有一个基数，基数为 X的进位计数制称为 X进制，表示每一个数位上的数运算时都是逢 X 进一。

常见进制

1. 十进制：0,1,2,3,4,5,6,7,8,90,1,2,3,4,5,6,7,8,9。

2. 二进制：0,10,1。

3. 八进制：0,1,2,3,4,5,6,70,1,2,3,4,5,6,7。

4. 十六进制： 0,1,2,3,4,5,6,7,8,90,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F

进制转换

非十进制转十进制

将非十进制数转成十进制数，只要将每个数位的加权和即可。

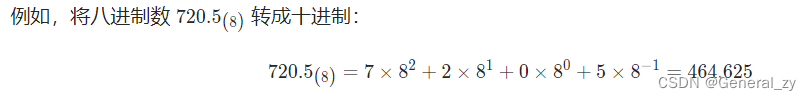
十进制转非十进制

将十进制数转成 XX 进制数，需要对整数部分和小数部分分别转换。

1. 对于整数部分，转换方式是将十进制数的整数部分每次除以 X直到变成 0，并记录每次的余数，反向遍历每次的余数即可得到 X进制表示。

2. 对于小数部分，转换方式是将十进制数的小数部分每次乘以 X直到变成 0，并记录每次的整数部分，正序遍历每次的整数部分即可得到 X 进制表示。

其他进制间的转换

1. 在两个不同的非十进制之间转换，常规的思路是先转成十进制数，再转成目标进制数。在一些特殊情况下，也可以不经过十进制，直接进行转换。
2. 例如，将二进制数转成八进制数或十六进制数，以及将八进制数或十六进制数转成二进制数，都不需要经过十进制。一位八进制数可以表示成三位二进制数，一位十六进制数可以表示成四位二进制数。
   

计算机中的二进制

1. 计算机采用的是二进制，二进制包括两个数码：0,1。
2. 一位二进制数的可能取值有 2 个，k位二进制数的可能取值就有 2^k个。

在计算机中有多种数据类型，表示整数的数据类型就有好几种：

1 字节数，即 8 位二进制数，可能取值有 2^8个；
2 字节数，即 16 位二进制数，可能取值有 2^16个；
类推......

32位机，寻址范围2^32，最大只能4G虚拟内存就是这个原因

有符号整数和无符号整数

1. 计算机中的数据类型包括有符号类型（整数）和无符号类型（正整数），有符号类型的整数称为有符号整数，无符号类型的整数称为无符号整数。

2. 有符号整数中，最高位用于表示符号，因此最高位又称符号位。当最高位是 0时表示 0或正整数，当最高位是 1时表示负整数。除了最高位以外的数位用于表示数字的大小。

3. 无符号整数中，所有的数位都用于表示数字的大小，因此无符号整数不存在负数。
   

原码、补码和反码

机器数和真值

1. 机器数：一个数在计算机中的二进制表示形式（有符号）
2. 真值：机器数的真正数值
3. 机器数的最高位是符号位，所以机器数的形式值不一定等于真正数值。

例如 10001010 的形式值是 138，真正数值是 -10

原码、反码和补码的概念

1. 原码：机器数的符号位加上机器数的真值的绝对值，最高位是符号位，其余位表示数值。
   以 8位二进制数为例。+10的原码是 00001010，-10的原码是10001010。

2. 反码
   0和正数的反码与原码相同，负数的反码是将原码的除了符号位之外的每一位取反。
   对于负数，反码的表示方式不直观，通常需要转换成原码才能计算其数值。

3. 补码
   0和正数的补码与原码、反码相同，负数的补码是在反码的基础上加 1 得到。
   对于负数，补码的表示方式不直观，通常需要转换成原码才能计算其数值。

4. 计算机中的表示

   • 反码的引入，解决了原码的减法运算结果错误的问题，但是仍然没有解决同时存在 +0 和 -0 的问题。
   • 补码的引入则同时解决了减法运算错误和同时存在 +0 和 -0的问题，而且可以多表示一个最小值。
   • 在补码表示法中，不存在 -0的情况。以 8位二进制数为例，0的补码是 00000000，10000000 表示的是 -128−128

位运算

位运算共有 6种，分别是：与、或、异或、取反、左移和右移，其中左移和右移统称移位运算，移位运算又分为算术移位和逻辑移位。

func main(){
	a:=0b10
	b:=0b11
	fmt.Println(a)
	fmt.Println(b)

	fmt.Println(a&b) //与
	fmt.Println(a|b) //或
	fmt.Println(a^b) //异或

	fmt.Println(^a) //反
	2
	3
	2
	3
	1
	-3
}

与、或、异或和取反

1. 与运算的符号是 &，运算规则是：对于每个二进制位，当两个数对应的位都为 1 时，结果才为 1，否则结果为 0。
2. 或运算的符号是 |，运算规则是：对于每个二进制位，当两个数对应的位都为 0 时，结果才为 0，否则结果为 1。
3. 异或运算的符号是 ∧ ，运算规则是：对于每个二进制位，当两个数对应的位相同时，结果为 0，否则结果为 1。
4. 取反运算的符号是 ∼，运算规则是：对一个数的每个二进制位进行取反操作，0 变成 1，1变成 0。。

移位运算

按照是否带符号分类可以分成算术移位和逻辑移位

• 逻辑移位：不考虑符号位，移位的结果只是数据所有的位数进行移位。
• 算术移位：算术是带有符号的数据，所以我们不能直接移动所有的位数，这可能会使得符号不正确。

1. 左移运算的符号是 <<。左移运算时，将全部二进制位向左移动若干位，高位丢弃，低位补 0。对于左移运算，算术移位和逻辑移位是相同的。

2. 右移运算的符号是 >>。右移运算时，将全部二进制位向右移动若干位，低位丢弃，高位的补位由算术移位或逻辑移位决定：

   • 算术右移时，高位补最高位；

   • 逻辑右移时，高位补 0。

在 Go 语言中，对于有符号整数的右移操作，使用的是算术右移（Arithmetic Shift Right）。算术右移会保留符号位的值，这意味着在右移过程中，左边空出的位会用符号位的原始值填充。对于负数，符号位是 1，因此算术右移会在左边填充 1；对于正数，符号位是 0，所以会填充 0。

当你对一个负数进行算术右移时，由于所有位（包括符号位）都是 1，右移后左边仍然会填充 1，因此结果仍然是一个所有位都是 1 的数，即 -1。

这里有一个关键点需要注意：^int64(0) 的结果是 -1，因为 ^ 操作符作为一元运算符时表示按位取反，它会将 0 的所有位取反，包括符号位，因此得到的是一个所有位都是 1 的数，即 -1 的补码表示。

当你对 -1（即 ^int64(0) 的结果）进行右移 63 位的操作时，由于 -1 是负数，其符号位是 1，算术右移会在左边填充 1，因此无论你移动多少位，结果都是 -1。

这就是为什么即使你对 -1 右移 63 位，结果仍然是 -1 的原因。这与逻辑右移（Logical Shift Right）不同，逻辑右移不考虑符号位，总是在左边填充 0，但在 Go 语言中，对有符号整数的右移操作总是算术右移。

Python 中没有专门的无符号整数类型。Python 的整数类型 int 是无限精度的，也就是说，它可以表示任意大小的整数，不受固定位宽的限制。这意味着在 Python 中，你不需要担心整数溢出或者整数的位宽。

由于 Python 的 int 类型可以表示任意大小的整数，当你对一个整数进行按位取反操作时，Python 会将其视为一个无限位宽的有符号整数，并且按位取反操作会影响所有的位，包括符号位。在 Python 中，按位取反操作是通过 ~ 运算符实现的。

例如，对于 0 的按位取反操作：

inverted = ~0
print(inverted)  # 输出: -1

这里，~0 的结果是 -1，因为在补码表示中，-1 的所有位都是 1。

当你对一个整数进行右移操作时，Python 会执行算术右移，保留符号位。例如：

shifted = inverted >> 63
print(shifted)  # 输出: -1

在这个例子中，-1 右移 63 位仍然是 -1，因为 Python 会在左边填充符号位（即 1），保持数值的符号不变。

由于 Python 的整数类型不受位宽限制，你不需要担心逻辑右移和算术右移的区别，也不需要担心无符号整数类型。这使得在 Python 中进行位运算时，你可以专注于逻辑操作，而不必担心底层的位宽和表示细节。

移位运算与乘除法的关系

1. 左移运算对应乘法运算。将一个数左移 k 位，等价于将这个数乘以 2^k。
2. 将一个数（算术）右移 k 位，和将这个数除以 2^k是不等价的

位运算的性质

1. a^a = 0
2. a^b ^a = b
   

例题

7进制

func convertToBase7(num int) string {
    if num == 0 {
        return "0"
    }
    var isMinus bool
    var ans string
    if num < 0 {
        isMinus = true
        num = -num
    }
    for num != 0 {
        ans = strconv.Itoa(num%7) + ans
        num /= 7
    }
    if isMinus {
        ans = "-" + ans
    }
    return ans
}

基本原理

0s 表示一串 0，1s 表示一串 1。

x ^ 0s = x      x & 0s = 0      x | 0s = x
x ^ 1s = ~x     x & 1s = x      x | 1s = 1s
x ^ x = 0       x & x = x       x | x = x

位 1 的个数

1. 编写一个函数，输入是一个无符号整数（以二进制串的形式），返回其二进制表达式中数字位数为 ‘1’ 的个数（也被称为汉明重量）。
2. 输入必须是长度为 32 的 二进制串 。

循环每一位

func hammingWeight(num uint32) int {
	count :=0
	for i:=0;i<32;i++{
		// 此处结果为uint32要转为int
		count+= int((num>>i)&1)
	}
	return count
}

位运算性质

对于整数 n，n & (n−1) 的结果为将 n 的二进制表示的最后一个 1 变成 0。

func hammingWeight(num uint32) int {
	count :=0
	for num!=0{
		num=num&(num-1)
		count++
	}
	return count
}

只出现一次的数字 II

给你一个整数数组 nums ，除某个元素仅出现 一次 外，其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。

菜鸡的做法（我的做法）：

func singleNumber(nums []int) int {
	counter:=make(map[int]int,len(nums))
	for _,val:=range nums{
		counter[val]++
	}
	for k,v :=range counter{
		if v==1{
			return k
		}
	}
	return -1
} 

大佬的做法：

使用变量ones 和twos 分别存储出现一次的元素的异或值以及出现两次的元素的异或值。考虑只有一个元素的情况，假设该元素为num，当该元素出现 0 次到 3 次时，ones 和 twos 的值变化如下：

出现 0 次时（即初始状态），ones=0，twos=0；

出现 1 次时，ones=num，twos=0；

出现 2 次时，ones=0，twos=num；

出现 3 次时，ones=0，twos=0，和出现 0 次时的值相同。

func singleNumber(nums []int) int {
	ones,twos:=0,0
	for _,val :=range nums{
		ones = ones^val & (^twos)
		twos = twos^val & (^ones)
	}
	return ones
} 

FQA

python中为什么number没有长度限制

struct PyLongObject{
long ob_refcnt;                // 引用计数，64位系统占8 bytes, 32位系统占4 bytes
struct_typeobject *ob_type;    // 类型指针，64位系统占8 bytes, 32位系统占4 bytes
long ob_size;                  // 数据部分int的个数，64位系统占8 bytes, 32位系统占4 bytes
unsigned int ob_digit[1];      // 64位系统占4 bytes * abs(ob_size); 32位系统占2 bytes * abs(ob_size);
};

对于64位Python:

ob_refcnt，ob_type，ob_size各占8字节。当ob_size为0时，ob_digit不存在，否则其字节数为4abs(ob_size)，所以最少为83=24字节，而且每次增量都是4的倍数。

对于32位Python:

ob_refcnt，ob_type，ob_size各占4字节。当ob_size为0时，ob_digit不存在，否则其字节数为2abs(ob_size)，所以最少为43=12字节，而且每次增量都是2的倍数。

采用这种处理方式，Python的整型变量基本上可做到无长度限制。

32位的CPU能进行int64位的数值计算吗？

能，但比起64位的CPU，性能会慢一些。

1. 64位的CPU在计算两个int64的数值相加时，可以将数据通过64位的总线，一次性存入到64位的寄存器，并在进行计算后返回到内存中。

2. 32位的CPU，虽然在代码里放了个int64的数值，但实际上CPU的寄存器根本放不下这么大的数据，因此最简单的方法是，将int64的数值，拆成前后两半，现在两个int64相加，就变成了4个int32的数值相加，并且后半部分加好了之后，拿到进位，才能去计算前面的部分，这里光是执行的指令数就比64位的CPU要多。所以理论上，会更慢些。

int32和int64？

int32也就是用4个字节，32位的内存去存储数据，int64也就是用8个字节，64位去存数据。这个数值就是刚刚CPU运行流程中放在内存里的数据。