一种不需递归的两点间所有路径的算法

• ps.这是我第三次作图、编辑这篇文章，之前都因为传图时卡死重新写，强烈要求能够自动保存。
• 之前在另一个账号发了个简单运用opencv实现图形化校园导游&地图导航系统 然而密码忘了……就发在这个账号和博客上了

话不多说，先放效果图（结合了opencv实现动态演示）

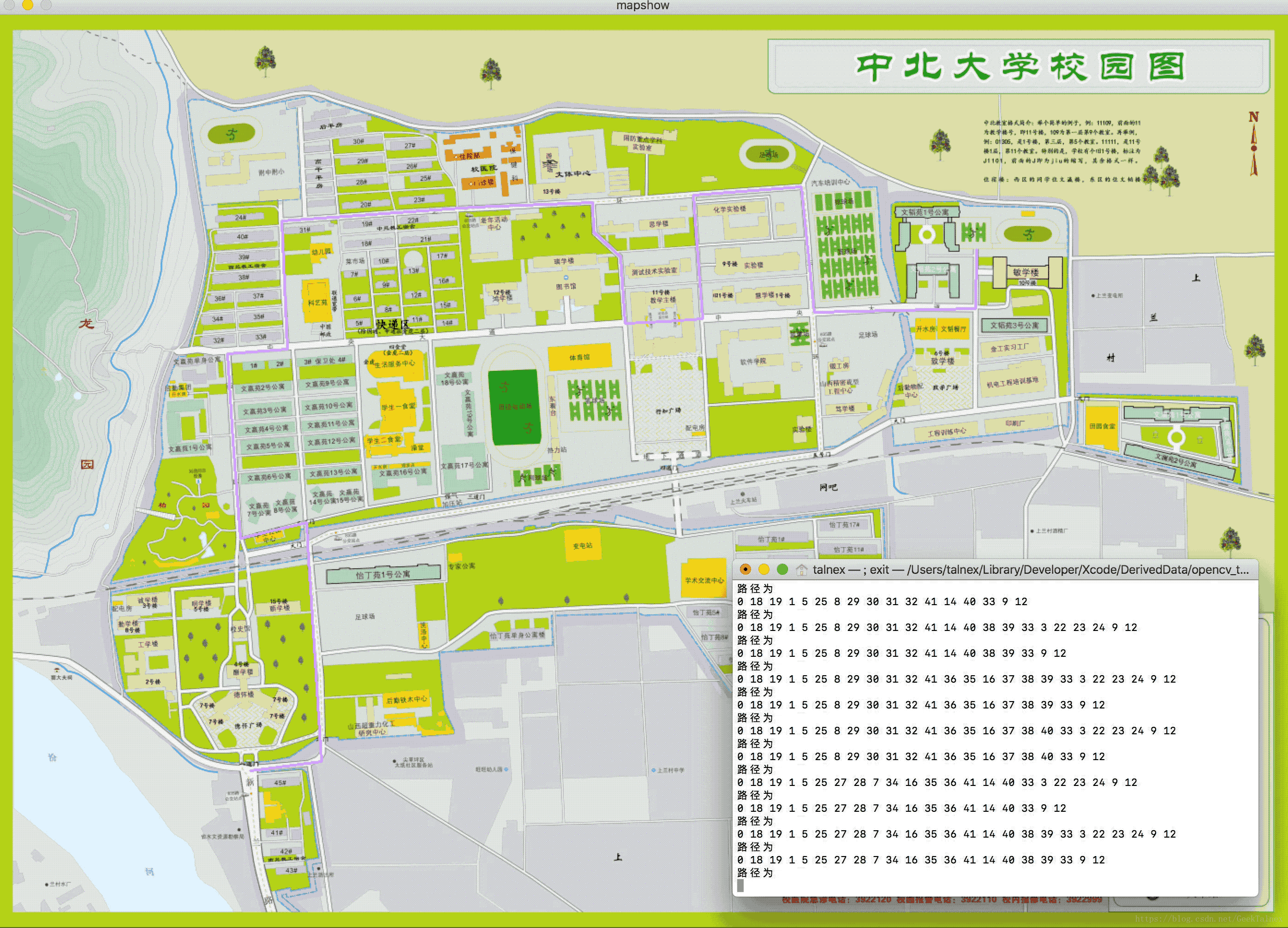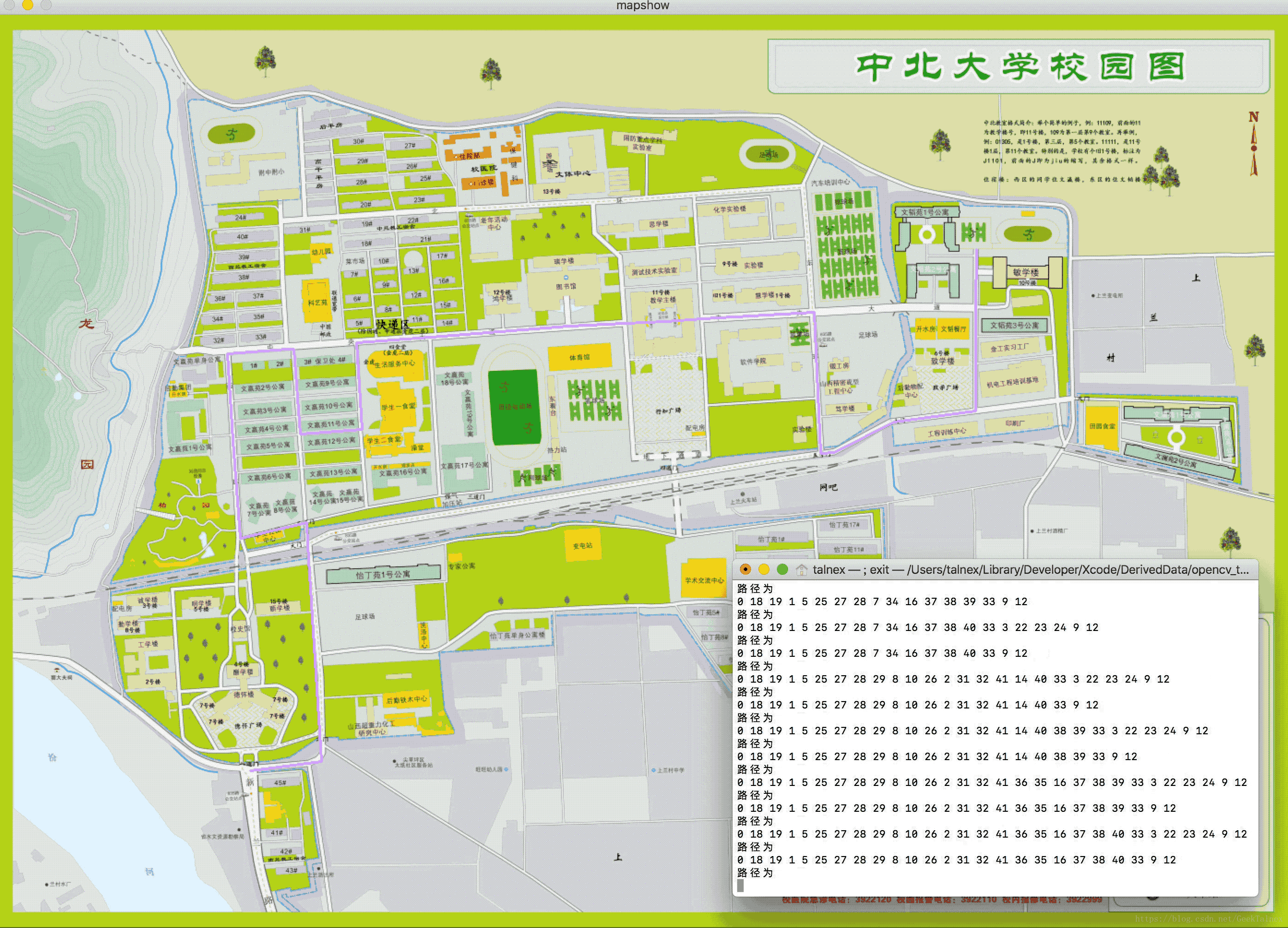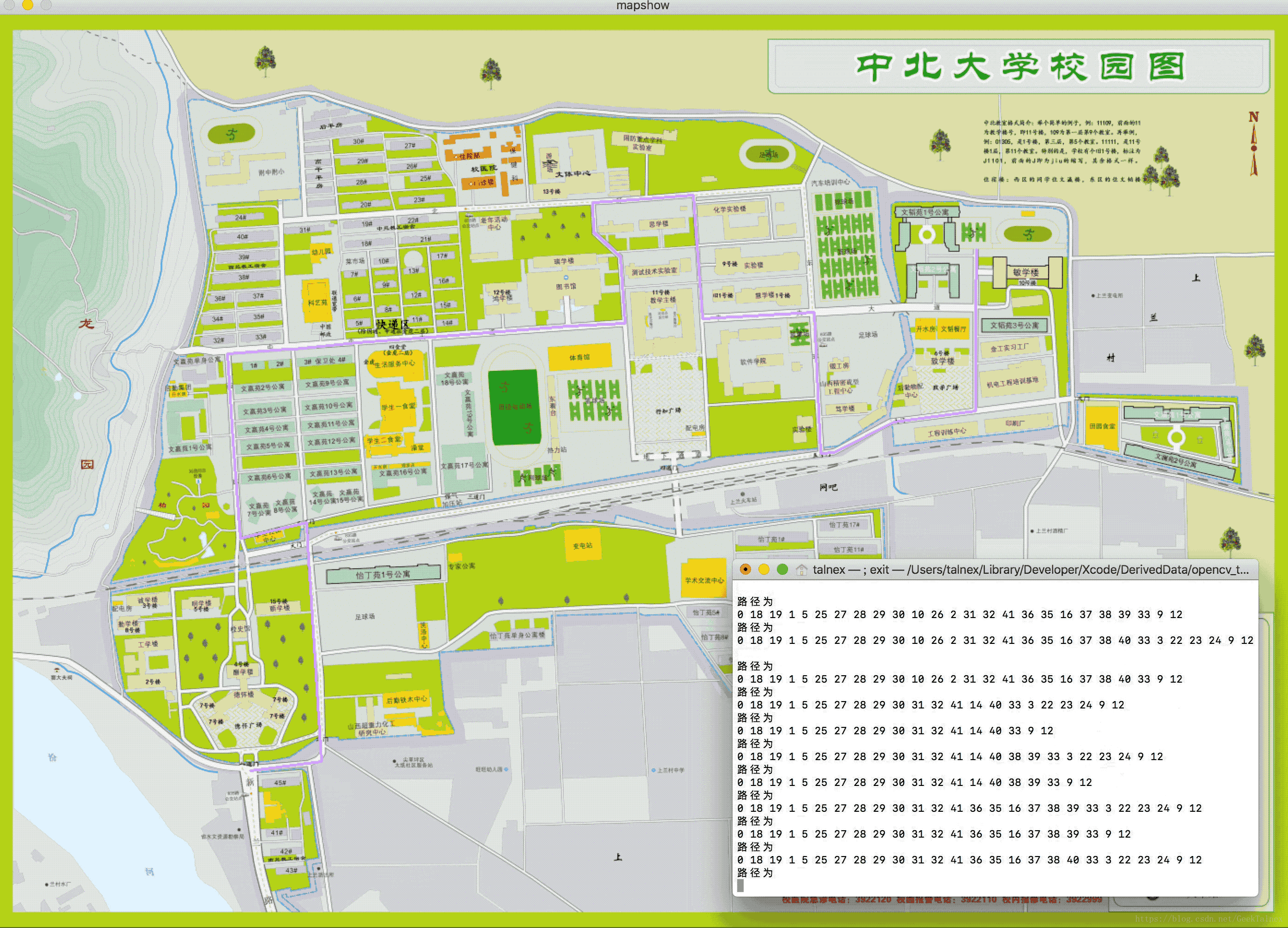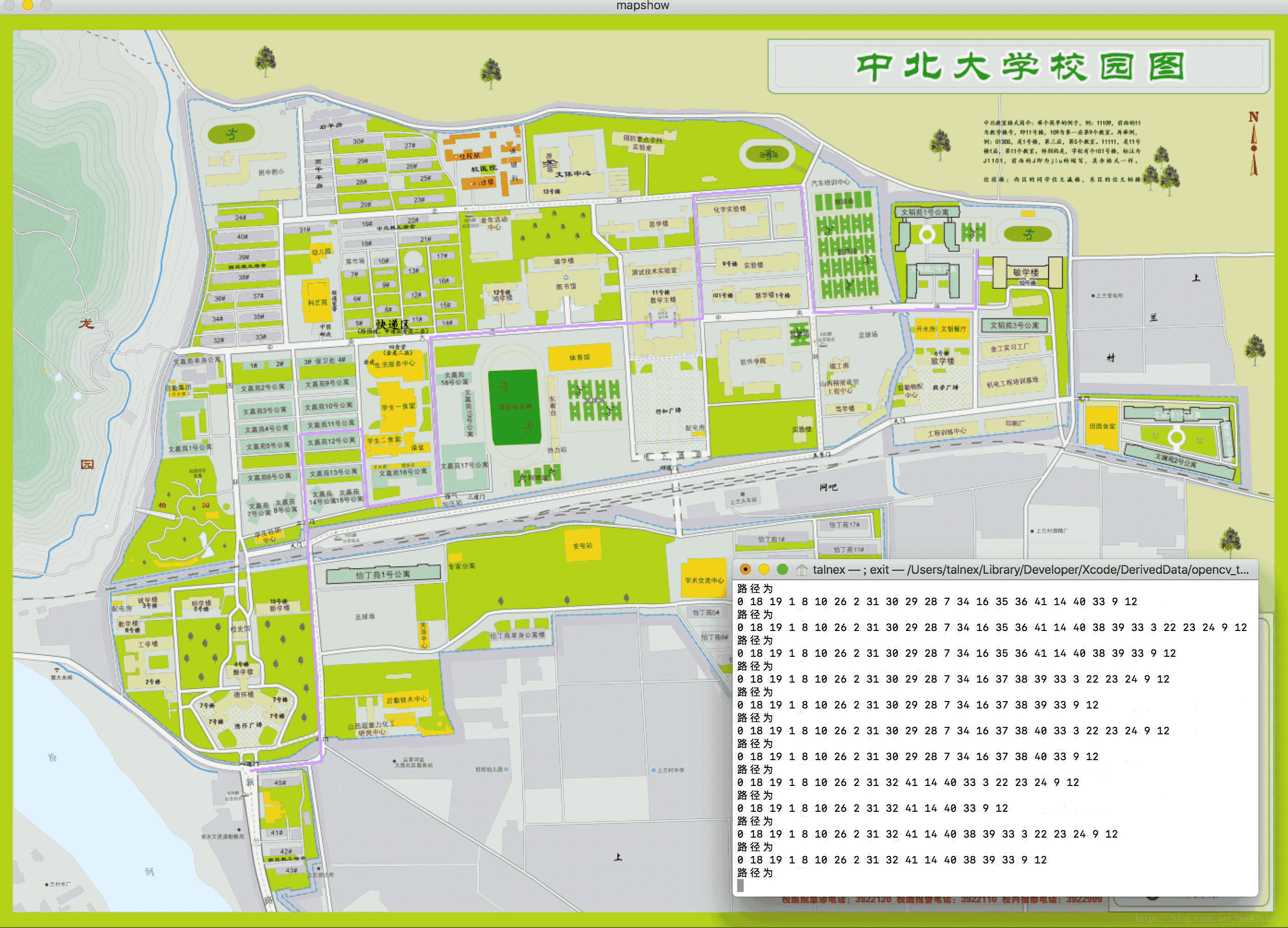
• 18个节点，一共大约是600条路径，能够全部找出并输出出来。

• 这里举一个例子介绍一下这个算法，其实两点间所有路径的算法有一个简短的多的递归算法，但是真的是不好理解，而且理论上这种递归了n层的算法效率也并不高，于是，这个只有一个循环，剩下的都是判断的奇葩算法就出现了，如下图所示，这里有一个图，其中有5个节点和7条边

• 我们将它的邻接矩阵表示出来，其中1代表可达，0代表不可达，为了能够正确地遍历路径，我们同时建立一个栈，如下图所示

注意：以下是图例介绍：
1、邻接矩阵的行号和列号与节点编号对应，如第0行代表0号节点对于其他节点的邻接关系
2、此邻接矩阵还同时代表了这个关系在Visited数组中的值，其中，空白表示还未访问过为初始值0，绿色底色表示值为1，同时为了演示过程方便，用橙色底色代表正在执行判断的关系
3、其实大多数操作理由都在图上标出来了，也会稍作讲解

---

下面让我们开始吧（多图预警）

• 首先我们分析一下需求，我们要实现输出两个点之间的所有路径，那么遍历整个图是难免的，图的遍历有两种算法，一种是深度优先遍历，一种是广度优先遍历，而我的思路是，使用深度优先遍历到一棵树的底部（终点），如果有分叉点就压入栈中保存，当遍历到终点，折返到上一个分叉点的另外一支进行遍历直到栈中没有没有访问的节点。

首先，选定一个起点和终点，以起点的编号为行号横着进行遍历。

• 在这里我们使用的是0号节点作为起点，2号节点作为终点，那么就从第0行开始，开始判断0号节点与周围节点的关系。
• 首先，根据图我们可以找出来从0到2的路线有：012,0132,032,0312,04312,0432

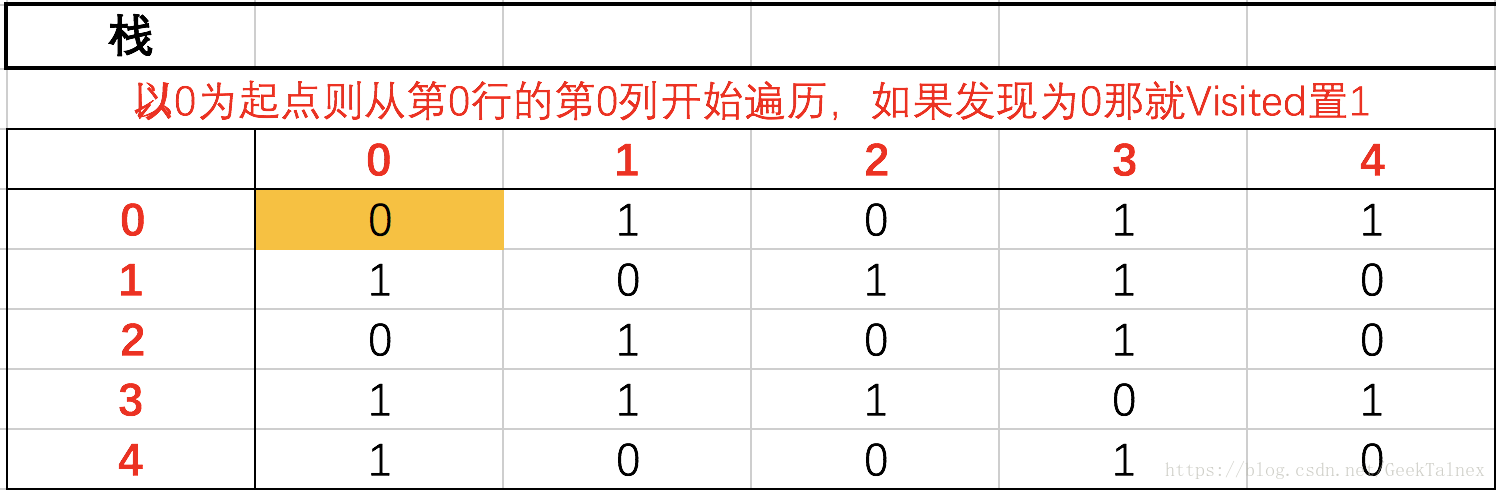
visited数组置1就代表了这个节点已经判断完了，遇到0就要置1。

遇到了连通的节点后会优先进入这个节点进行遍历，这就是深度优先，压栈就是为了以后这一棵子树遍历完后能返回遍历另外的子树。

每进入一行就要从这一行的第一列开始遍历，跳过的规则有这些
1、如果Visited为1，直接跳过
2、如果栈中有这个编号，直接跳过
3、如果数组值为0，相应Visited数组置1，相当于直接跳过
相应的理由为：
1、访问过了
2、防止成环或者出现双向箭头的路径（去了又回）
3、没有路径相连

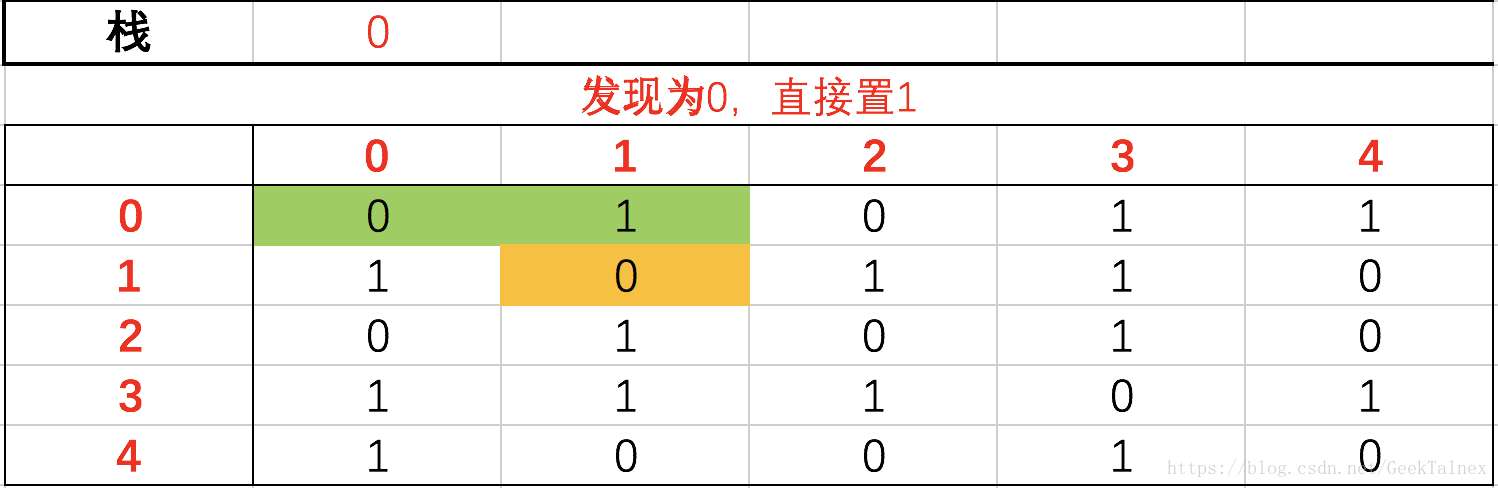
先判断栈中有就跳过，没有就判断visited，是1就跳过，是0再看邻接矩阵的值如果为0，visited置1，如果为1，判断是不是终点，如果是终点就输出，如果不是终点就进入对应行。
找到终点的列号时，压栈行号和列号就是一条完整的路径。

• 在实际中就是这样的了：

• 在实际中就是这样的了：
  

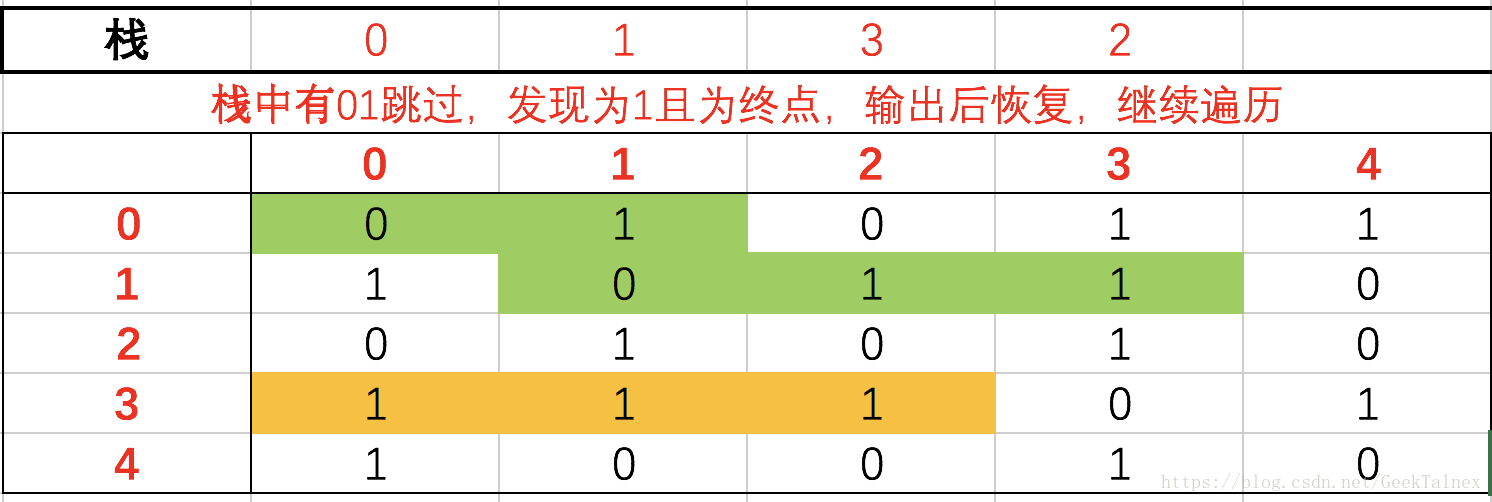
• 于是又找到了一条路径：

• 在实际中就是这样的了：

• 其实我们人眼一眼就能看出来进入4后没有路径，但是计算机还是需要遍历判断后才行的

这一步跳的有点多，首先进入了4行，发现栈中有013，则跳过了013，在24列时由于值为0所以直接置1。

这里说一下为什么出栈后要把本行刷新，其实很容易理解，比如当一棵左子树被访问完了后，如果不对他的所有节点进行重置，在对其右子树访问时如果遇到其子节点与左子树的某节点有连通关系，正常情况下应该进入这个节点继续遍历，然而由于没有刷新，导致之前访问左子树的节点时所有的Visited数组都为1，所以会丢失这些路径。

这里跳了好几步，首先刷新了4行出栈进入了3行，跳过了01，234Visited都为1也跳过，所以3行也遍历完了，所以刷新3行出栈进入1行，跳过了0列，发现123的Visited为1也跳过，所以现在在判断1行4列。

由于1行已遍历完，刷新、出栈进入了0行，在0行中由于01列Visited为1所以跳过，2列值为0，置1后继续遍历3列，发现为1，所以压栈、进入3行，在实际中是这样的：

• 在实际中是这样的：
  

• 找到了一条路径：

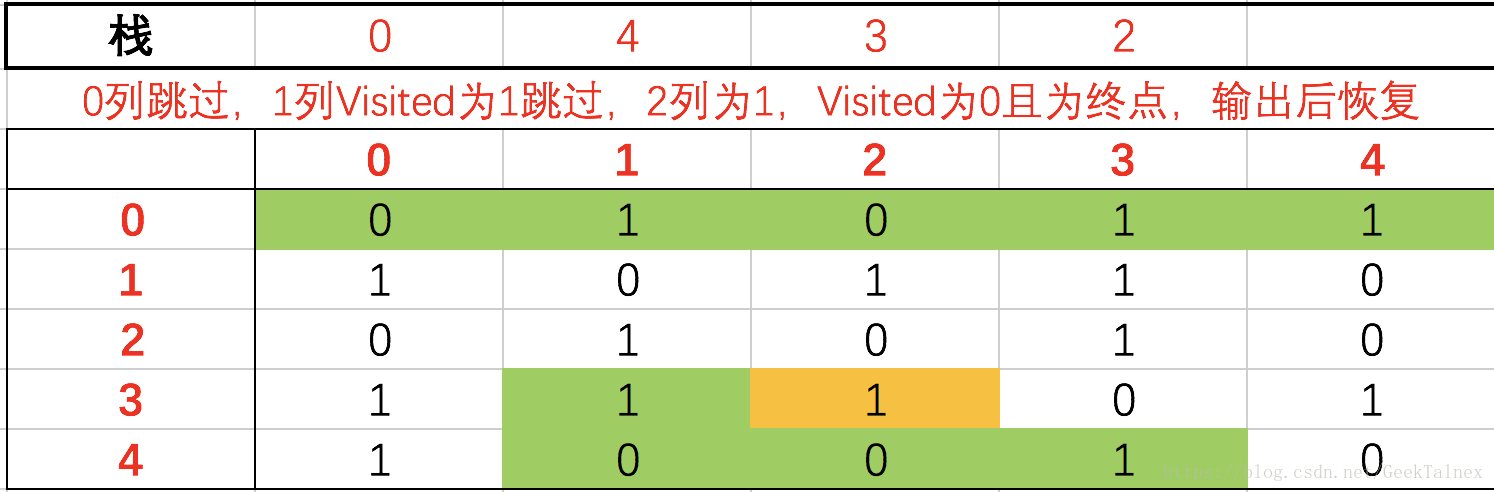
• 进入4了后其实也没有路径：

这两张就是0列跳过，12列置1，3列跳过，4列置1，遍历完了刷新本行，出栈，进入3行后Visited都为1所以继续刷新、出栈、进入了0行，0123列的Visited都为1所以都跳过，进入4行，压栈。

进入4行后栈中有0跳过0列，12列值为0置1，3列为1压栈进入3行，栈中有0，跳过0列，发现1列为1，压栈、进入1行。

---

剩下的就只放矩阵图了啊，其实动手在纸上一画就清楚了~

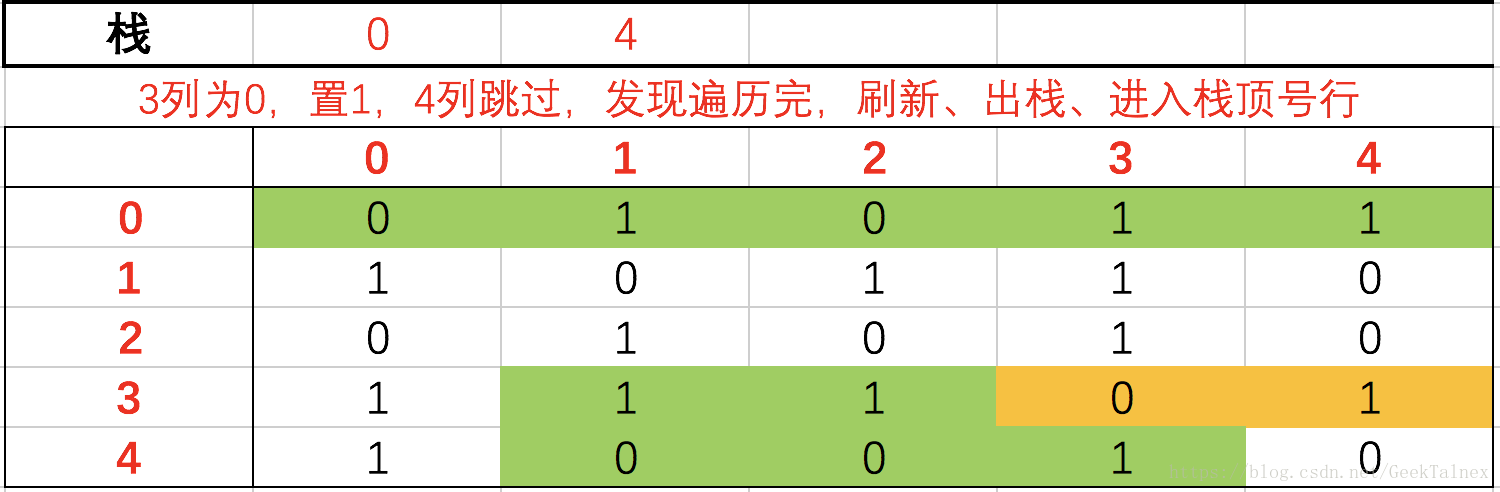
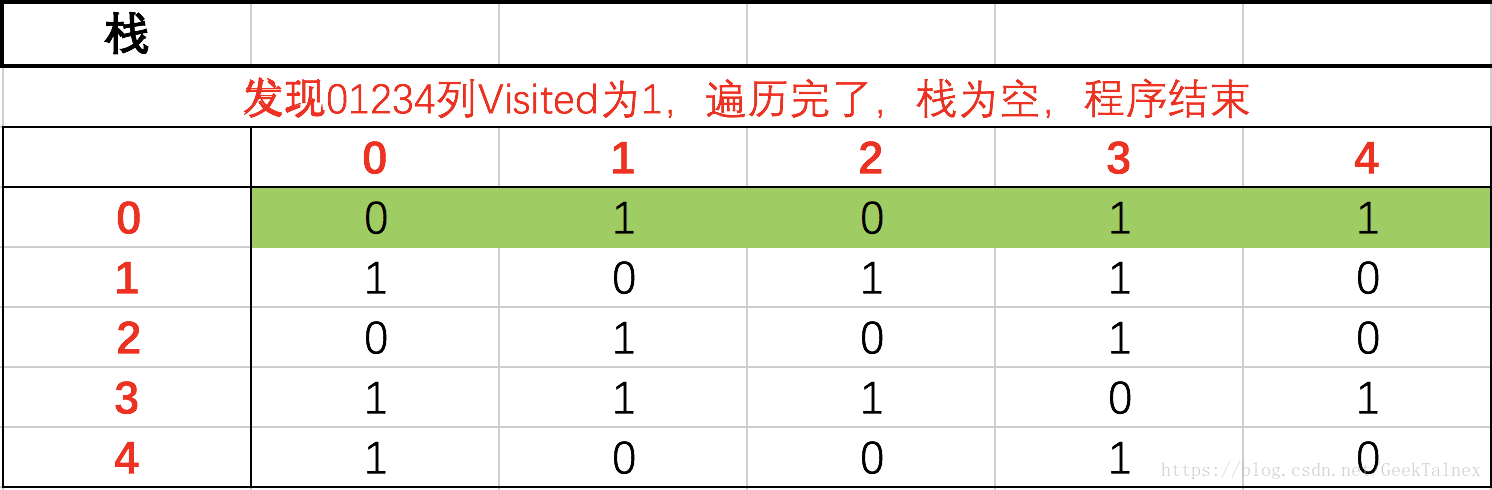
当时画的流程图，看看就好……

代码部分

理解整个程序的关键就在于注意a和i的赋值操作，进入哪一行是由a决定的，遍历这一行的哪一列是由i决定的，当i=-1时经过一遍循环体的i++就变成0了，也就是从0列开始遍历，而出栈时栈顶值是赋值给a的，这样在下一次循环体时a值改变，遍历的就是更改后的行了。
整个判断关系是分先后的，因为比较复杂后来就没有进行优化。

void DFS(int a,int b){
        for (int i=0; i<NUM_POINTS; i++) {
            if (!Matrix[a][i]) {
                visited[a][i]=1;
                visited[i][a]=1;
                if (i==NUM_POINTS-1) {
                    if (!s.is_empty()) {
                        for (int j=0; j<NUM_POINTS; j++) {
                            visited[a][j]=0;
                        }
                        path.pop();
                        a=s.pop();
                        i=-1;
                        continue;
                    }
                    else ;
                }
                else continue;
            }
            else{
                if (!visited[a][i]) {
                    if (s.do_have(i)){
                        if (i==NUM_POINTS-1) {
                            if (!s.is_empty()) {
                                for (int j=0; j<NUM_POINTS; j++) {
                                    visited[a][j]=0;
                                }
                                path.pop();
                                a=s.pop();
                                i=-1;
                                continue;
                            }
                            else ;
                        }
                        else continue;
                    }
                    else {
                        if(i==b){
                            visited[a][i]=1;
                            visited[i][a]=1;
                            path.push(a);
                            path.push(i);
                            NUM_ALLPATHS++;//修改这里
                            show_s(path,a,b);//修改这里
                            path.pop();
                            path.pop();
                            if (i==NUM_POINTS-1) {
                                if (!s.is_empty()) {
                                    for (int j=0; j<NUM_POINTS; j++) {
                                        visited[a][j]=0;
                                    }
                                    path.pop();
                                    a=s.pop();
                                    i=-1;
                                    continue;
                                }
                                else ;
                            }
                            else continue;
                        }
                        else{
                            visited[a][i]=1;
                            visited[i][a]=1;
                            path.push(a);
                            s.push(a);
                            a=i;
                            i=-1;
                            continue;
                        }
                    }
                }
                else {
                    if(i==NUM_POINTS-1){
                        if (!s.is_empty()) {
                            for (int j=0; j<NUM_POINTS; j++) {
                                visited[a][j]=0;
                            }
                            path.pop();
                            a=s.pop();
                            i=-1;
                            continue;
                        }
                        else ;
                    }
                    else continue;
                }
            }
        }
        cout<<"路径的数量为："<<NUM_ALLPATHS<<endl;
    }