AcWing第 77 场周赛

进球

两支足球队之间展开了一场足球赛。

整场比赛双方一共打进了 n 粒进球，进球多的一方将收获最终的胜利。

请你根据进球纪录，判断哪支球队最终获胜。

保证不存在平局。

输入格式

第一行包含整数 n。

接下来 n 行，其中第 i 行记录了打进第 i 粒进球的球队的名称。

球队名称由大写字母构成，长度范围 [1,10]。

保证输入中包含的不同球队不超过两支。

输出格式

输出最终获胜队伍的名称。

数据范围

前 5 个测试点满足 1≤n≤5。
所有测试点满足 1≤n≤100。

输入样例1：

1
ABC

输出样例1：

ABC

输入样例2：

5
A
ABA
ABA
A
A

输出样例2：

A

#include<bits/stdc++.h>
using namespace std;
typedef pair<string, int>Pair;

bool cmp(const Pair&a, const Pair&b) {
    return a.second > b.second;//大顶
}

int main() {
    int n;
    while (~scanf("%d", &n) && n) {
        vector<Pair>PairVec;
        map<string, int>m;
        for (int i = 0;i < n;i++) {
            string c;
            cin >> c;++m[c];//插入键  值默认为0（作为计数器）
        }
        for (map<string, int>::iterator it = m.begin();it != m.end();++it) {
            PairVec.push_back(make_pair(it->first, it->second));
        }
        sort(PairVec.begin(), PairVec.end(), cmp);
        cout << PairVec.front().first << endl;
    } 
} 

 

环形队伍 

n 个小朋友围成一圈，按顺时针顺序依次编号为 1∼n。

有 7 种颜色的帽子，每种颜色的帽子的数量都足够多。

7 种颜色不妨表示为 R、O、Y、G、B、I、V。

现在，要给每个小朋友都发一个帽子，要求：

• 每种颜色的帽子都至少有一个小朋友戴。
• 任意四个相邻小朋友的帽子颜色都各不相同。

请你提供一种分发帽子的方案。

输入格式

共一行，包含一个整数 n。

输出格式

输出一行长度为 n 的由代表颜色的字符组成的字符串，其中的第 i 个字符表示第 i 个小朋友分到的帽子的颜色。

如果方案不唯一，输出任意合理方案均可。

数据范围

所有测试点满足 7≤n≤100。

输入样例1：

8

输出样例1：

ROYGRBIV

输入样例2：

13

输出样例2：

ROYGBIVGBIVYG

#include<bits/stdc++.h>
using namespace std;
int n;
const string s = "ROYGBIV";
int main(){
    cin >> n;
    for(int i=0; i <= n - 4; i++) putchar(s[i % 4]);
    for(int i=4; i <= 6; i++) putchar(s[i]);
    return 0;
}

 

摆放棋子 

给定一个 n×mn×m 的国际象棋棋盘（即一个 n×mn×m 的方格矩阵）。

我们知道传统国际象棋中，主教（象）的行走规则是只能斜走，格数不限。

现在，我们对主教进行了加强，不妨称加强后的主教为大主教。

大主教仍然只能斜走，格数不限，但是当其走到棋盘边缘的方格时，它可以发生反射并继续移动。

更具体地说，当它到达棋盘边（但并非角）上的方格时，它可以将移动方向改变 9090 度并继续移动，当它到达棋盘角上的方格时，它可以将移动方向改变 180180 度并继续移动。

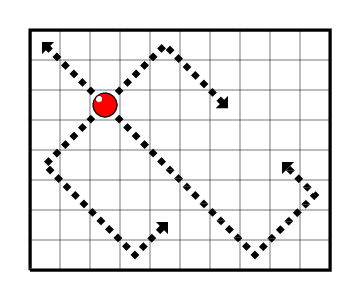
如果一个棋子可以到达另一个棋子所在的方格，则认为该棋子可以攻击到另一个棋子。

我们希望在给定的棋盘中摆放尽可能多的大主教，但是要求它们两两之间不能攻击到对方。

请你计算，最多可以摆放多少个大主教。

输入格式

共一行，包含两个整数 n,mn,m。

输出格式

一个整数，表示可以摆放的大主教的最大可能数量。

数据范围

前 66 个测试点满足 2≤n,m≤42≤n,m≤4。
所有测试点满足 2≤n,m≤1062≤n,m≤106。

输入样例1：

3 4

输出样例1：

2

输入样例2：

3 3

输出样例2：

3

新知识：__gcd 函数可以直接算出最大可能的数量！其他方法会比较复杂，如模拟或动态，应为方格的数量不确定，直接用gcd函数。

#include<bits/stdc++.h>
using namespace std;

int main()
{
    int n,m;
    cin>>n>>m;
    cout<<__gcd(n-1,m-1)+1;
}