哥伦比亚大学Coursera课程Natural Language Processing：Quiz 2: covers material from weeks 3 and 4

Quiz 2: covers material from weeks 3 and 4Help Center

Warning: The hard deadline has passed. You can attempt it, but you will not get credit for it. You are welcome to try it as a learning exercise.

In accordance with the Coursera Honor Code, I  certify that the answers here are my own work.

Question 1

Say we have a context-free grammar with start symbol S, and the following rules:

• S  →  NP VP
• VP  →  Vt NP
• Vt  →  saw
• NP  →  John
• NP  →  DT NN
• DT  →  the
• NN  →  dog
• NN  →  cat
• NN  →  house
• NN  →  mouse
• NP  →  NP CC NP
• CC  →  and
• PP  →  IN NP
• NP  →  NP PP
• IN  →  with
• IN  →  in

How many parse trees do each of the following sentences have under this grammar? 

1. John saw the cat and the dog
2. John saw the cat and the dog with the mouse
3. John saw the cat with the dog and the mouse

Write your answer as 3 numbers separated by spaces. For example if you think sentence 1 has 2 parses, sentence 2 has 5 parses, and sentence 3 has 3 parses, you would write 

2 5 3

Answer for Question 1

Question 2

Say we have a PCFG with start symbol S, and the following rules with associated probabilities:

• q(S  →  NP VP) = 1.0
• q(VP  →  Vt NP) = 1.0
• q(Vt  →  saw) = 1.0
• q(NP  →  John) = 0.25
• q(NP  →  DT NN) = 0.25
• q(NP  →  NP CC NP) = 0.3
• q(NP  →  NP PP) = 0.2
• q(DT  →  the) = 1.0
• q(NN  →  dog) = 0.25
• q(NN  →  cat) = 0.25
• q(NN  →  house) = 0.25
• q(NN  →  mouse) = 0.25
• q(CC  →  and) = 1.0
• q(PP  →  IN NP) = 1.0
• q(IN  →  with) = 0.5
• q(IN  →  in) = 0.5

Now assume we have the following sentence:

• John saw the cat and the dog with the mouse

Which of these statements is true?

All parse trees for the sentence have the same probability under the PCFG

At least two parse trees for the sentence have different probabilities under the PCFG

Question 3

Consider the CKY algorithm for parsing with PCFGs. The usual recursive definition in this algorithm is as follows: 

π(i,j,X)=maxs∈{i…(j−1)}X→YZ∈R,(q(X→YZ)×π(i,s,Y)×π(s+1,j,Z))  

Now assume we'd like to modify the CKY parsing algorithm to that it returns the maximum probability for any *left-branching* tree for an input sentence. Here are some example left-branching trees: 

It can be seen that in left-branching trees, whenever a rule of the form X  →  Y Z is seen in the tree, then the non-terminal Z must directly dominate a terminal symbol. 

Which of the following recursive definitions is correct, assuming that our goal is to find the highest probability left-branching tree?

π(i,j,X)=maxs∈{i…(j−1)}X→YZ∈R,(q(X→YZ)×π(i,s,Y)×π(s+1,j,Z))

π(i,j,X)=maxX→YZ∈R(q(X→YZ)×π(i,j−1,Y)×π(j,j,Z))

π(i,j,X)=maxs∈{(i+1)…(j−1)}X→YZ∈R,(q(X→YZ)×π(i,s,Y)×π(s+1,j,Z))

π(i,j,X)=maxX→YZ∈R(q(X→YZ)×π(i,i,Y)×π(i+1,j,Z))

Question 4

What are the head words for the following constituents? 

a) The NP "the man" 

b) The PP "with the telescope" 

c) The VP "saw the dog with the telescope" 

d) The S "the man saw the dog with the telescope" 

Write the answer as four words separated by spaces, for example 

the with saw the

Answer for Question 4

Question 5

Say we have a PCFG with start symbol S, and rules and probabilities as follows: 

q(S→a)=0.3  

q(S→a S)=0.7  

For any sentence  x=x1…xn , define  T(x)  to be the set of parse trees for  x  under the above PCFG. For any sentence  x , define the probability of the sentence under the PCFG to be 

p(x)=∑t∈T(x)p(t)  

where  p(t)  is the probability of the tree under the PCFG. 

Now assume we'd like to define a bigram language model with the same distribution over sentences as the PCFG. What should be the parameter values for  q(a|∗) ,  q(a|a) , and  q(STOP|a)  so that the bigram language model gives the same distribution over sentences as the PCFG? 

(For this question assume that the PCFG does not need to generate STOP symbols: for example the sentence "a a a" in the PCFG translates to the sentence "a a a STOP" in the bigram language model.) 

Write your answer as a sequence of three numbers, for example 

0.1 0.2 0.1

Answer for Question 5

Question 6

Say we have a PCFG with the following rules and probabilties:

• q( S  →  NP VP ) = 1. 0

• q( VP  →  Vt NP ) = 0. 2

• q( VP  →  VP PP ) = 0. 8

• q( NP  →  NNP ) = 0. 8

• q( NP  →  NP PP ) = 0. 2

• q( NNP  →  John ) = 0. 2

• q( NNP  →  Mary ) = 0. 3

• q( NNP  →  Sally ) = 0. 5

• q( PP  →  IN NP ) = 1. 0

• q( IN  →  with ) = 1. 0

• q( Vt  →  saw) = 1. 0

Now say we use the CKY algorithm to find the highest probability parse tree under this grammar for the sentence

• John saw Mary with Sally

We use tparser to refer to the output of the CKY algorithm on this sentence.

(Note: assume here that we use a variant of the CKY algorithm that can return the highest probability parse under this grammar - don't worry that this grammar is not in Chomsky normal form, assume that we can handle grammars of this form!)

The gold-standard (human-annotated) parse tree for this sentence is

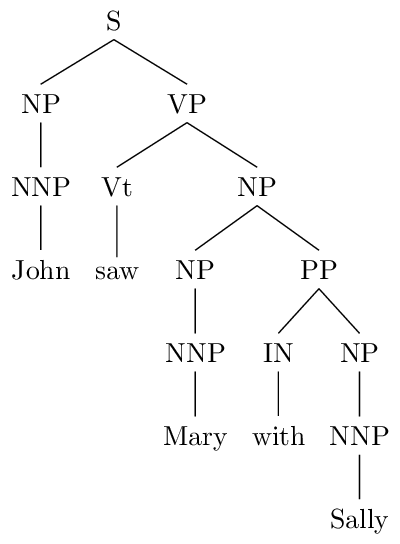
What is the precision and recall of tparser (give your answers to 3 decimal places)?

Write your answer as a sequence of numbers: for example “0.3 0.8” would mean that your precision is 0.3, your recall is 0.8.

Here each non-terminal in the tree, excluding parts of speech, gives a "constituent" that is used in the definitions of precision and recall. For example, the gold-standard tree shown above has 7 constituents labeled S, NP, VP, NP, NP, PP, NP respectively (we exclude the parts of speech NNP, IN, and Vt).