香农熵理论 Shannon Entropy

Shannon Entropy

The Shannon entropy equation provides a way to estimate the average minimum number of bits needed to encode a string of symbols, based on the frequency of the symbols.

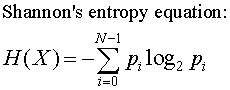
In the Shannon entropy equation, pi is the probability of a given symbol.

To calculate log2 from another log base (e.g., log10 or loge):

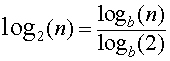
The minimum average number of bits is per symbol is

If we have a symbol set {A,B,C,D,E} where the symbol occurance frequencies are:

   A = 0.5
   B = 0.2
   C = 0.1
   D = 0.1
   E = 0.1

The average minimum number of bits needed to represent a symbol is

  H(X) = -[(0.5log20.5 + 0.2log20.2 + (0.1log20.1)*3)]
  H(X) = -[-0.5 + (-0.46438) + (-0.9965)]
  H(X) = -[-1.9]
  H(X) = 1.9

Rounding up, we get 2 bits/per symbol. To represent a ten character string AAAAABBCDE would require 20 bits if the string were encoded optimally. Such an optimal encoding would allocate fewer bits for the frequency occuring symbols (e.g., A and B) and long bit sequences for the more infrequent symbols (C,D,E).

This example is borrowed from A Guide to Data Compression Methods by Solomon. Note that the frequence of the symbols also happens to match the frequence in the string. This will not usually be the case and it seems to me that there are two ways to apply the Shannon entropy equation:

1. The symbol set has a known frequency, which does not necessarily correspond to the frequency in the message string. For example, characters in a natural language, like english, have a particular average frequency. The number of bits per character can be calculated from this frequency set using the Shannon entropy equation. A constant number of bits per character is used for any string in the natural language.

2. Symbol frequency can be calculated for a particular message. The Shannon entropy equation can be used calculate the number of bits per symbol for that particular message.

Shannon entropy provides a lower bound for the compression that can be achieved by the data representation (coding) compression step. Shannon entropy makes no statement about the compression efficiency that can be achieved by predictive compression. Algorithmic complexity (Kolmogorov complexity) theory deals with this area. Given an infinite data set (something that only mathematicians possess), the data set can be examined for randomness. If the data set is not random, then there is some program that will generate or approximate it and the data set can, in theory, be compressed.

Note that without an infinite data set, this determination is not always possible. A finite set of digits generated for a pi expansion satisify tests for randomness. However, these digits must be pseudo-random, since they are generated from a deterministic process. Algorithmic complexity theory views a pi expansion of any number of digits as compressible to the function that generated the sequence (a relatively small number of bits).

Ian Kaplan
August 2002
Revised:

Back to Lossless Wavelet Compression

Back to Wavelets and Signal Processing

---

Shannon Entropy

The Shannon entropy equation provides a way to estimate the average minimum number of bits needed to encode a string of symbols, based on the frequency of the symbols.

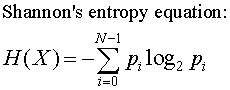
In the Shannon entropy equation, pi is the probability of a given symbol.

To calculate log2 from another log base (e.g., log10 or loge):

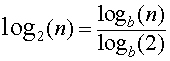
The minimum average number of bits is per symbol is

If we have a symbol set {A,B,C,D,E} where the symbol occurance frequencies are:

   A = 0.5
   B = 0.2
   C = 0.1
   D = 0.1
   E = 0.1

The average minimum number of bits needed to represent a symbol is

  H(X) = -[(0.5log20.5 + 0.2log20.2 + (0.1log20.1)*3)]
  H(X) = -[-0.5 + (-0.46438) + (-0.9965)]
  H(X) = -[-1.9]
  H(X) = 1.9

Rounding up, we get 2 bits/per symbol. To represent a ten character string AAAAABBCDE would require 20 bits if the string were encoded optimally. Such an optimal encoding would allocate fewer bits for the frequency occuring symbols (e.g., A and B) and long bit sequences for the more infrequent symbols (C,D,E).

This example is borrowed from A Guide to Data Compression Methods by Solomon. Note that the frequence of the symbols also happens to match the frequence in the string. This will not usually be the case and it seems to me that there are two ways to apply the Shannon entropy equation:

1. The symbol set has a known frequency, which does not necessarily correspond to the frequency in the message string. For example, characters in a natural language, like english, have a particular average frequency. The number of bits per character can be calculated from this frequency set using the Shannon entropy equation. A constant number of bits per character is used for any string in the natural language.

2. Symbol frequency can be calculated for a particular message. The Shannon entropy equation can be used calculate the number of bits per symbol for that particular message.

Shannon entropy provides a lower bound for the compression that can be achieved by the data representation (coding) compression step. Shannon entropy makes no statement about the compression efficiency that can be achieved by predictive compression. Algorithmic complexity (Kolmogorov complexity) theory deals with this area. Given an infinite data set (something that only mathematicians possess), the data set can be examined for randomness. If the data set is not random, then there is some program that will generate or approximate it and the data set can, in theory, be compressed.

Note that without an infinite data set, this determination is not always possible. A finite set of digits generated for a pi expansion satisify tests for randomness. However, these digits must be pseudo-random, since they are generated from a deterministic process. Algorithmic complexity theory views a pi expansion of any number of digits as compressible to the function that generated the sequence (a relatively small number of bits).

Ian Kaplan
August 2002
Revised:

Back to Lossless Wavelet Compression

Back to Wavelets and Signal Processing

---