神经网络中的网络优化和正则化（一）之学习率衰减和动态梯度方向

本文链接：https://blog.youkuaiyun.com/Gamer_gyt/article/details/100996744

转载请注明出处：https://thinkgamer.blog.youkuaiyun.com/article/details/100996744
博主微博：http://weibo.com/234654758
Github：https://github.com/thinkgamer
公众号：搜索与推荐Wiki

引言

神经网络中的网络优化和正则化问题介绍主要分为一，二，三，四篇进行介绍。

第一篇包括
- 网络优化和正则化概述
- 优化算法介绍
第二篇包括
- 参数初始化
- 数据预处理
- 逐层归一化
第三篇包括
- 超参数优化
第四篇包括
- 网络正则化

概述

虽然神经网络有比较强的表达能力，但是应用神经网络到机器学习任务时仍存在一些问题，主要分为：

网络优化

神经网络模型是一个非凸函数，再加上神经网络中的梯度消失和梯度爆炸，很难进行优化，另外网络的参数比较多，且数据量比较大导致训练效率比较低。

正则化

神经网络拟合能力强，容易在训练集上产生过拟合，需要一些正则化的方法来提高网络的泛化能力。

从大量的实践经验看主要是从网络优化和正则化两个方面提高学习效率并得到一个好的网络模型。

在低维空间的非凸优化问题中主要是存在一些局部最优点，基于梯度下降优化算法会陷入局部最优点，因此低维空间的非凸优化的难点在于如何选择合适的参数和逃离局部最优点。

深层神经网络中参数较多，其是在高维空间的非凸优化问题中，和低维空间的非凸优化有些不同，其主要难点在于如何逃离鞍点（Saddle Point），鞍点的梯度为0，但是在一些维度上是最高点，在另一些维度上是最低点，如下图所示（图1-1）：
鞍点示例

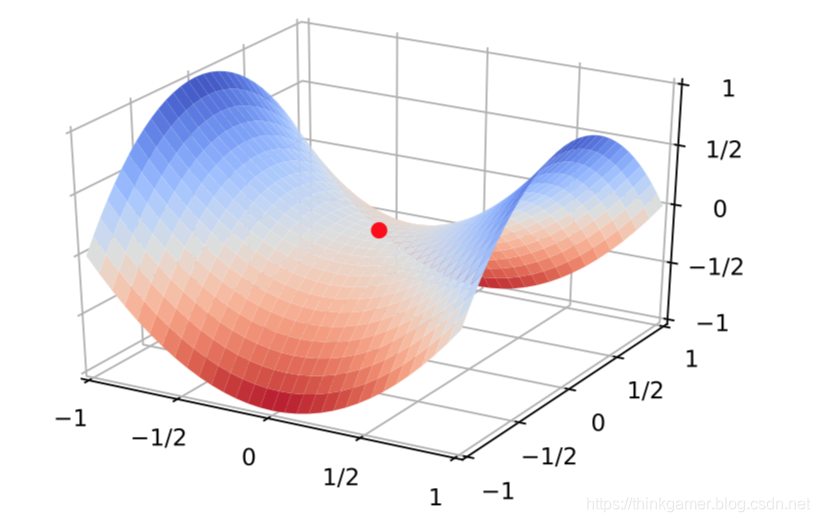
在高维空间中，局部最优点要求在每一维度上都是最低点，这种概率很低，假设网络有1000
个参数，每一维上取得局部最优点的最小概率为p，则在整个参数空间中取得局部最优点的最小概率为 $p^{1000}$ ，这种概率很小，也就是说在整个参数空间中，大部分梯度为0的点都是鞍点。

优化算法介绍

深层神经网络的参数学习主要是通过梯度下降算法寻找一组最小结构的风险参数，梯度下降分为：

批量梯度下降
随机梯度下降
小批量梯度下降

根据不同的数据量和参数量，可以选择一种合适的梯度下降优化算法，除了在收敛效果和效率上的区别，这三种梯度下降优化算法还存在一些共同问题（具体会在下一篇进行详细介绍）：

如何初始化参数
预处理数据
如何选择合适的学习率，避免陷入局部最优

在训练深层神经网络时，通常采用小批量梯度下降算法。令 $f(x,\theta)$ 为一个深层神经网络， $\theta$ 为网络参数，使用小批量梯度优化算法时，每次选择K个训练样本 $I_t =\left \{ (x^t,y^t) \right \} , t \in (1,T)$ ，第t次迭代时损失函数关于 $\theta$ 的偏导数为（公式1-1）：
$g_t(\theta ) = \frac{ 1 }{ K } \sum_{ (x^t,y^t) \in I_t} \frac{ \partial L(y^t,f(x^t, \theta)) }{ \partial \theta }$

第t次更新的梯度 $g'_t$ 定义为（公式1-2）：
$g_t'(\theta)= g_t(\theta_{t-1})$
使用梯度下降来更新参数（公式1-3）：
$\theta_t = \theta_{t-1} - \alpha g'(\theta)$
一般批量较小时，需要选择较小的学习率，否则模型不会收敛。下图（图1-2）给出了在Mnist数据集上批量大小对梯度的影响。从图1-2(a)可以看出，批量大小设置的越大，下降的越明显，并且下降的比较平滑，当选择批量的大小为1时，整体损失呈下降趋势，但是局部比较震荡。从图1-2(b)可以看出，如果按整个数据集上的迭代次数（Epoch）来看损失变化情况，则是批量样本数越小，下降效果越明显。

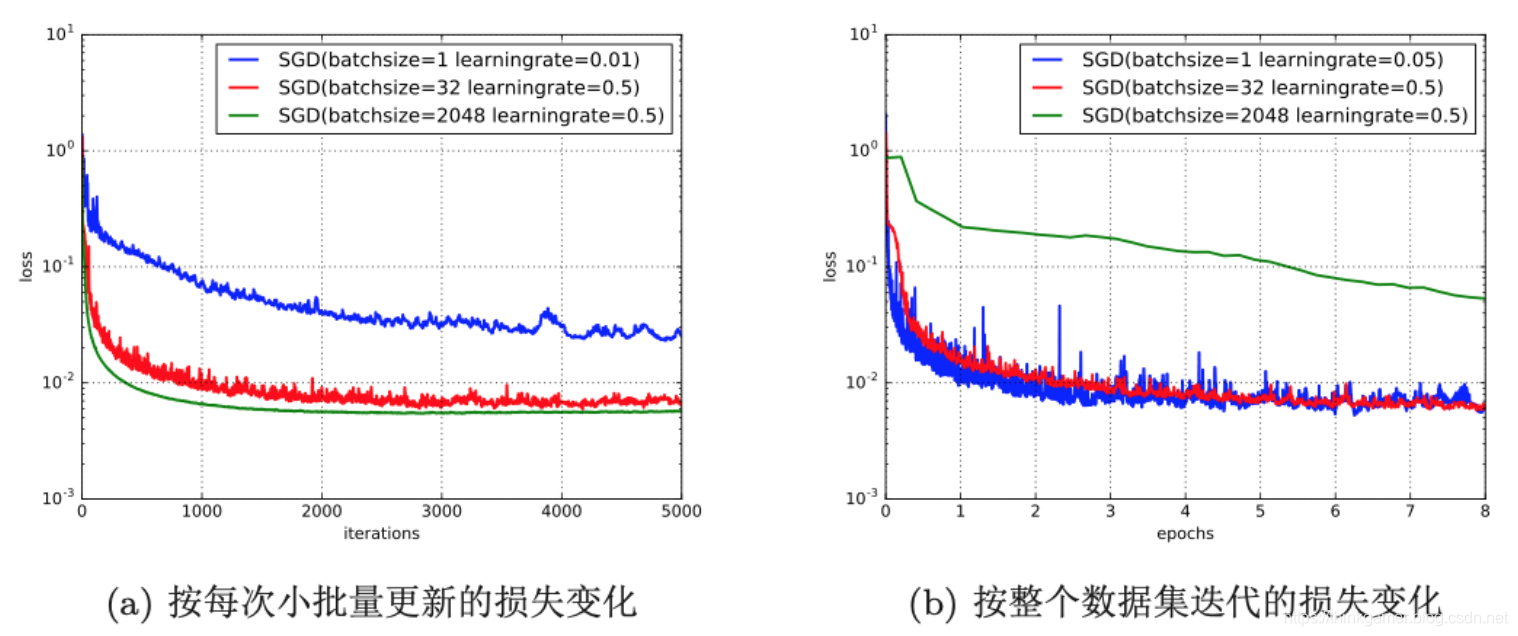
批量的大小对梯度的影响

为了更加有效的训练深层神经网络，在标准的小批量梯度下降算法中，经常使用一些改进方法加快优化速度，常见的改进方法有两种：

学习率衰减
梯度方向优化

这些改进的优化方法也同样可以应用在批量梯度下降算法和随机梯度下降算法。

学习率衰减

在梯度下降中，学习率的设置很重要，设置过大，则不会收敛，设置过小，则收敛太慢。从经验上看，学习率在一开始要设置的大些来保证收敛速度，在收敛到局部最优点附近时要小些来避免震荡，因此比较简单的学习率调整可以通过学习率衰减（Learning Rate Decay）的方式来实现。假设初始学习率为 $\alpha_0$ ，第t次迭代的学习率为 $a_t$ ，常用的衰减方式为按照迭代次数进行衰减，例如

逆时衰减（公式1-4）

$a_t = a_0 \frac{1 }{ 1 + \beta t}$

指数衰减（公式1-5）

$a_t = a_0\beta^t$

自然指数衰减（公式1-6）

$a_t = a_0 exp(-\beta * t)$
其中 $\beta$ 为衰减率，一般为0.96

AdaGrad

AdaGrad（Adaptive Gradient）算法是借鉴L2正则化的思想，每次迭代时自适应的调整每个参数的学习率。AdaGrad的参数更新公式为（公式1-7）：
$G_t = \sum_{t=1}^{T} g_t \odot g_t \\ \bigtriangleup \theta_t = - \frac{\alpha }{ \sqrt{G_t + \epsilon } } \odot g_t \\ g'_t(\theta) = g_t(\theta_{t-1}) + \bigtriangleup \theta_t$
其中 $\alpha$ 为学习率， $\epsilon$ 是为了保证数据稳定性而设置的非常小的常数，一般取值是 $e^{-7}$ 到 $e^{-10}$ ，这里的开平方，加，除运算都是按照元素进行的操作。

在AdaGrad算法中，如果某个参数的偏导数累积比较大，其学习率相对较小，相反，如果其偏导数累积比较大，其学习率相对较大。但是整体上随着迭代次数的增加，学习率逐渐减小。

AdaGrad算法的缺点是在经过一定次数的迭代后依然没有找到最优点，由于这时候的学习率已经很小了，就很难找到最优点。

RMSProp

RMSProp是Geoff Hinton提出的一种自适应学习率的方法，可以在有些情况下避免AdaGrad的学习率单调递减以至于过早衰减的缺点。

RMSProp算法首先计算的是每次迭代速度 $g_t$ 平方的指数衰减移动平均，如下所示（公式1-8）：
$G_t = \beta G_{t-1} + (1-\beta) g_t \odot g_t = (1- \beta) \sum_{t=1}^{T} \beta ^{T-t} g_t \odot g_t$
其中 $\beta$ 为衰减率，一般取值为0.9，RMSProp算法参数更新公式为（公式1-9）：
$\bigtriangleup \theta_t = - \frac{\alpha }{ \sqrt{G_t + \epsilon } } \odot g_t \\ g'_t(\theta) = g_t(\theta_{t-1}) + \bigtriangleup \theta_t$
其中 $\alpha$ 为学习率，通常为0.001。

从公式1-8 可以看出，RMSProp和AdaGrad的区别在于 $G_t$ 的计算由累积方式变成了指数衰减移动平均，在迭代过程中，每个参数的学习率并不是呈衰减趋势，即可以变大，也可以变小。

AdaDelta

AdaDelta算法也是AdaGrad算法的一个改进，和RMSProp算法类似，AdaDelta算法通过梯度平方的指数衰减移动平均来调整学习率，除此之外，AdaDelta算法还引入了每次参数更新差 $\bigtriangleup \theta$ 的平方的指数衰减移动平均。

第t次迭代时，每次参数更新差 $\bigtriangleup \theta_t , 1<t<T-1$ 的指数衰减移动平均为（公式1-10）：
$\bigtriangleup X^2_{t-1} =\beta _1 \bigtriangleup X^2_{t-2} + (1 - \beta) \bigtriangleup \theta_{t-1} \odot \bigtriangleup \theta_{t-1}$
其中 $\beta_1$ 为衰减率，AdaDelta算法的参数更新差值为（公式1-11）：
$\bigtriangleup \theta_t = - \frac{\sqrt {\bigtriangleup X^2_{t-1} + \epsilon }}{ \sqrt {G_t + \epsilon}} g_t$

其中 $G_t$ 的计算方式和RMSProp算法一样。从公式1-11可以看出，AdaDelta算法将RMSProp算法中的初始学习率 $\alpha$ 改为动态计算的 $\sqrt {\bigtriangleup X^2_{t-1} + \epsilon }$ ，在一定程度上减缓了学习旅率的波动。

梯度方向优化

除了调整学习率外，还可以使用最近一段时间内的平均梯度来代替当前时刻的梯度来作为参数的更新方向，从图1-2中可以看出，在小批量梯度下降中，如果每次选取样本数量比较小，损失就会呈现震荡的方式下降，有效的缓解梯度下降中的震荡的方式是通过用梯度的移动平均来代替每次的实际梯度。并提高优化速度，这就是动量法。

动量法

动量法（Momentum Method）是用之前积累的动量来替代真正的梯度，每次替代的梯度可以看作是加速度。

在第t次迭代时，计算负梯度的“加权移动平均”作为参数的更新方向，如下所示（公式1-12）：
$\bigtriangleup \theta_t = \rho \bigtriangleup \theta_{t-1}-\alpha g_t$
其中 $\rho$ 为动量因子，通常设置为0.9， $\alpha$ 为学习率。

参数的实际更新值取决于最近一段时间内梯度的加权平均值。当某个参数在最近一段时间内梯度方向不一致时，参数更新的幅度变小，相反，参数更新的幅度变大，起到加速的作用。

一般而言，在迭代初期，梯度的更新方向比较一致，动量法会起到加速作用，可以更快的起到加速的作用，可以更快的到达最优点，在迭代后期，梯度的更新方向不一致，在收敛时比较动荡，动量法会起到减速作用，增加稳定性。从某种程度来讲，当前梯度叠加上部分的上次梯度，一定程度上可以看作二次梯度。

Nesterov加速梯度

Nesterov加速梯度（Nesterov Accelerated Gradient， NAG）也叫Nesterov动量法（Nesterov Momentum），是一种对动量法的改进。

在动量法中，实际的参数更新方向 $\bigtriangleup \theta_t$ 为上一步的参数更新方向 $\bigtriangleup \theta_{t-1}$ 和当前的梯度 $g_t$ 的叠加，这样， $\bigtriangleup \theta_t$ 可以拆分为两步进行，先根据 $\bigtriangleup \theta_{t-1}$ 更新一次得到参数 $\tilde{\theta }$ ，再用 $g_t$ 进行更新，如下所示（公式1-13）：
$\tilde{\theta } = \theta_{t-1} + \rho \bigtriangleup \theta_{t-1} \\ \theta_t = \tilde{\theta } - \alpha g_t$

其中 $g_t$ 为点 $\theta_{t-1}$ 上的梯度，所以第二步不太合理，更合理的更新方向为 $\tilde{\theta }$ 上的梯度，这样合并后的更新方向为（公式1-14）：
$\bigtriangleup \theta_t = \rho \bigtriangleup \theta_{t-1} -\alpha g_t(\theta_{t-1} + \rho \bigtriangleup \theta_{t-1} )$
其中 $g_t(\theta_{t-1} + \rho \bigtriangleup \theta_{t-1} )$ 表示损失函数在 $\tilde{\theta } = \theta_{t-1} + \rho \bigtriangleup \theta_{t-1}$ 上的偏导数。

下图（图1-3）给出了动量法和 Nesterov 加速梯度在参数更新时的比较：

动量法和 Nesterov 加速梯度在参数更新时的比较

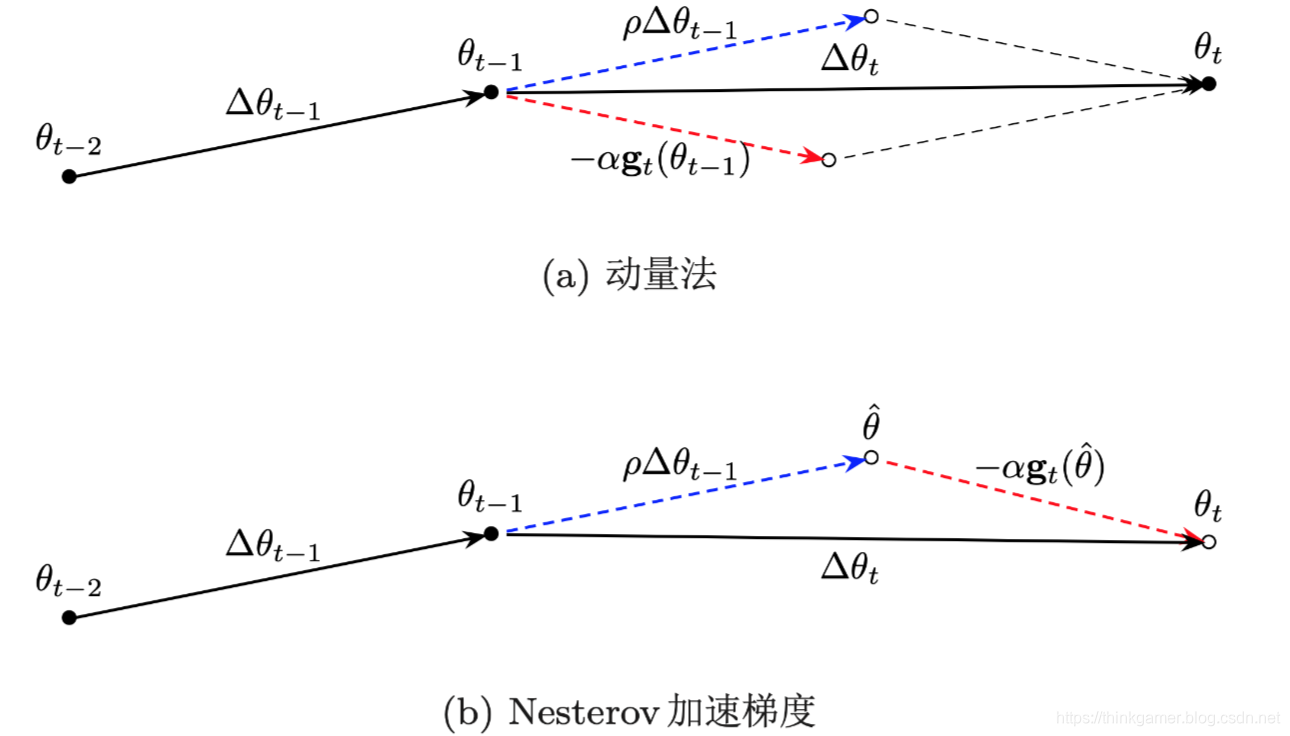
AdaM算法

自适应动量估计算法（Adaptive Moment Estimation，Adam）可以看作是动量法和RMSprop的结合，不但使用动量作为参数更新，而且可以自适应调整学习率（公式1-15）。
$M_t = \beta _1M_{t-1} + (1-\beta _1)g_t \\ G_t = \beta _2 G_{t-1} + (1-\beta _2)g_t \odot g_t$
其中 $\beta_1 ，\beta_2$ 分别为两个移动平均的衰减率，通常取值： $\beta_1=0.9,\beta_2=0.99$ 。

$M_t$ 可以看作是梯度的均值（一阶矩）， $G_t$ 可以看作是梯度的未减去均值的方差（二阶矩）。

假设 $M_t =0,G_t=0$ ，那么在迭代初期， $M_t，G_t$ 的值会比真实的均值和方差要小，特别是当 $\beta_1 ，\beta_2$ 都接近1时，偏差会很大，因此需要对偏差进行修正，如下所示（公式1-16）：
$\tilde{M_t} = \frac{M_t}{ 1 - \beta^t _1} \\ \tilde{G_t} = \frac{G_t}{ 1 - \beta^t _2}$
Adam算法的更新差值为（公式1-17）：
$\bigtriangleup \theta_t = - \frac{\alpha }{\sqrt{ \tilde{G_t} + \varepsilon }} \tilde{M_t}$
其中学习率 $\alpha$ 通常设置为0.001，并且也可以进行衰减，比如 $a_t = \frac{a_0} { \sqrt{t}}$ 。