Python数据结构与算法 DAY 03 快速排序&插入排序&二分法查找&二叉函数节点以及数的创建&二叉树深度遍历

Python数据结构与算法 DAY 03 重点知识总结 快速排序&插入排序&二分法查找&二叉函数节点以及数的创建&二叉树深度遍历

一 快速排序

快速排序需要注意的一点是它的思想 每一次排序会将比中间数大的数放在中间数的左边 并且将比中间数大的数放在中间数的右边 每一次取的中间数都是列表的第一个数 并采用递归的思想完成

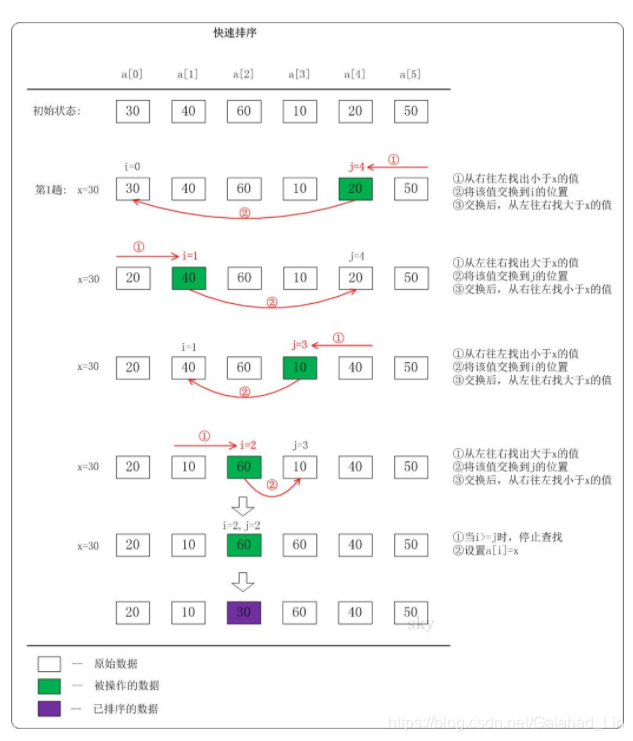
代码表示如下:
这里需要注意一个部分 外部大循环和内部的小循环 如果内部不加小循环 那么将会报错 根据逻辑来说需要仔细考虑内层循环的条件

def quick_sort(lst,start,end):
    if start >= end:
        return
    # 设定三个游标
    low = start
    high = end
    mid = lst[start]

    # 设立外层循环 主要目的 将数据分为mid左边的数据小于mid mid右边的数据大于mid
    while low<high:
        # 设立内层循环 先从high开始 判断数字大小 如果数字大于mid 则移动游标
        # 如果数字小于mid 则将该数 赋值与左边游标
        while low<high and lst[high] >= mid:
            high -= 1

        lst[low] = lst[high]
        # 设立内层循环 由于赋值为low low将开始向右移动 同样分为两种情况
        while low<high and lst[low] <= mid:
            low += 1
        lst[high] = lst[low]

    # 跳出循环的时候证明 high和low 的游标已经指向同一个了
    lst[high] = mid

    # 使用递归的思想 mid左边和右边的数进行快速排序
    quick_sort(lst,start,low-1)
    quick_sort(lst,low+1,end)

lst = [54,26,93,17,77,31,44,55,20]
quick_sort(lst,0,len(lst)-1)
print(lst)

快速排序的时间复杂度

1. 最优时间复杂度 : O(nlogn)
2. 最坏时间复杂度 : O(n^2)
3. 稳定性 : 不稳定

插入排序

插入排序是一种简单直观的排序算法 它的工作原理是通过构建有序序列 对未排序的数据 在已排序序列中从后向前扫描 找到相应的位置进行插入 插入排序在实现上 在从后向前扫描过程中 需要反复把已有元素逐步向后挪位 为最新元素提供空间

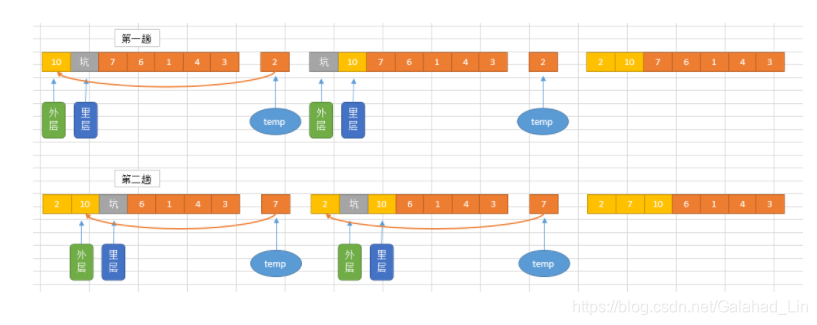
代码实现如下:

def insert_sort(alist):
    # 从第二个位置，即下标为1的元素开始向前插入
    for i in range(1, len(alist)):
        # 从第i个元素开始向前比较，如果小于前一个元素，交换位置
        for j in range(i, 0, -1):
            if alist[j] < alist[j-1]:
                alist[j], alist[j-1] = alist[j-1], alist[j]

alist = [54,26,93,17,77,31,44,55,20]
insert_sort(alist)
print(alist)

插入排序的时间复杂度:

1. 最优时间复杂度:O(n) (升序排列 序列已经处于升序的状态)
2. 最坏时间复杂度: O(n^2)
3. 稳定性 : 稳定

三 常见的排序算法的效率比较

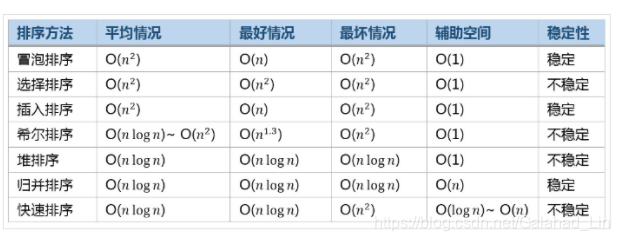
四 搜索&二分法查找

搜索是在一个项目集合中找到一个特定项目的算法过程 搜索通常的答案是真的或者假的 因为该项目是否存在 搜索最常见的方法是: 顺序查找 二分法查找 二叉树查找 哈希查找

一 二分法查找

二分法查找又称为折半查找 优点是比较次数少 查找速度快 平均性能号 其缺点事要求待查表格为有序表 且插入删除复杂 因此折半查找方法不适用于经常变动而查找频繁的有序列表

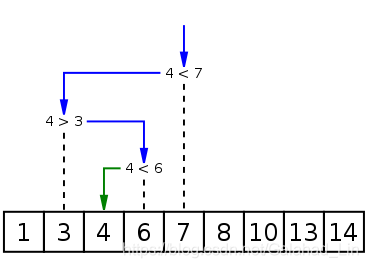
二分法查找的实现可以分为不使用迭代实现和使用迭代实现

1. 非迭代方法
   这里需要注意的是最外层的while循环的条件

def scaning_without(lst,number):
    start = 0
    end = len(lst) -1
    while start <= end :
        mid = (start + end + 1) // 2
        if lst[mid] == number:
            return True
        elif number < lst[mid]:
            end = mid-1
        else: # number > lst[mid]:
            start += 1
    return False

2. 迭代方法
   这里需要注意一下迭代的停止条件

def scaning_within(lst,number,start, end):
    if start>end:
        return False
    mid = (start + end ) // 2
    if lst[mid] == number:
        return True
    else:
        if number < lst[mid]:
            end = mid - 1
            scaning_within(lst,number,start,end)
        else: # number > lst[mid]:
            start = mid + 1
            scaning_within(lst,number,start,end)

五 树和树的算法

1. 树的特点
   
2. 树的术语
   
3. 树的种类
   

二叉树的节点表示以及树的创建

class Node():
    def __init__(self,elem):
        self.elem = elem
        self.lchild = None
        self.rchild = None

class Tree(object):
    """树类"""
    def __init__(self, root=None):
        self.root = root

    def add(self, elem):
        """为树添加节点"""
        node = Node(elem)
        #如果树是空的，则对根节点赋值
        if self.root == None:
            self.root = node
        else:
            queue = []
            queue.append(self.root)
            #对已有的节点进行层次遍历
            while queue:
                #弹出队列的第一个元素
                cur = queue.pop(0)
                if cur.lchild == None:
                    cur.lchild = node
                    return
                elif cur.rchild == None:
                    cur.rchild = node
                    return
                else:
                    #如果左右子树都不为空，加入队列继续判断
                    queue.append(cur.lchild)
                    queue.append(cur.rchild)

if __name__ == '__main__':
    t = Tree()
    t.add(10)