考研数学——高数：定积分

最新推荐文章于 2025-06-20 15:32:05 发布

原创最新推荐文章于 2025-06-20 15:32:05 发布 · 1.1k 阅读

·

23

·

CC 4.0 BY-SA版权

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

文章标签：

#考研数学 #高数

考研复习同时被 2 个专栏收录

16 篇文章

订阅专栏

16 篇文章

订阅专栏

本文详细讲解了高数中的定积分概念，包括微积分基本公式、定理和牛顿-莱布尼兹公式。通过证明积分中值定理，并探讨定积分在几何上的应用，如求平面图形的面积、旋转体的体积和曲线的弧长。文章通过例题加深读者对定积分的理解和应用。

目录

微积分基本公式

定理3（牛顿——莱布尼兹公式）

证明积分中值定理

定积分在几何上的应用

一、平面图形的面积

求曲线所围面积①

求曲线所围面积②

求曲线所围面积③

求曲线所围面积④

1.旋转体的体积

2.平行截面积已知的立体的体积

3.平面曲线的弧长

微积分基本公式

定理1

设 f(x) 在[a，b]上连续，则在[a，b]上 $\int_{a}^{x}f(t)dt$ 有 $(\int_a^{x}f(t)dt)' = f(x)$

定理2

设 f(x) 在[a，b]上连续，则在[a，b]上 $\int_{a}^{x}f(t)dt$ 是 f (x)的一个原函数

辅助理解

        这个求导是对于x求导，如果积分的下限为一个常数a，那么求导之后必定为0，所以不需要管这部分的结果，

        而对于上限是关于x的，求得它导数之前进行了一次积分相互抵消，所以结果就是原函数；如果上限是关于x的函数，求得的也会是关于这个函数的导数，利用F'x = F'u * U'x可得复合的结果

而对于下限如果是关于x的，（此时上限考虑为常数），那么结果实际上只用添一个负号就可以转化为变上限的形式；

所以可以推导出一般的公式：           $(\int_{\varphi (x)}^{\psi (x)}f(t)dt )' = f(\psi (x))*\psi '(x) - f(\varphi (x))*\varphi' (x)$

这个公式也能解释，如果上限或下限为常数时（与求导变量无关时），结果只会有一项

例题

$(1)\lim_{x\rightarrow 0}\frac{\int_{0}^{sin^2x}ln(1+t)dt}{x\sqrt{x^3-1}}$

提示：这题需要利用等价无穷小的多次替换，结合洛必达法则（这时候由于有积分，可以利用上面的定理公式进行求解）

定理3（牛顿——莱布尼兹公式）

设F（x）为连续函数f（x）在[a，b]上的一个原函数，则

$\int_{a}^{b}f(x)dx = F(b)-F(a)$

证明积分中值定理

求证：若 f (x) 在 [a，b]上连续，则 $\int_{a}^{b}f(x)dx = f(\xi )(b-a),a<\xi<b$

证明主要用到的方法： F'(x) = f(x) 与牛顿莱布尼兹公式

$\int_{a}^{b}f(x)dx = F(b)-F(a) = F'(\xi )(b-a) = f(\xi)(b-a)$

定积分在几何上的应用

能用定积分解决的问题的特征：

1、非均匀连续分布在[a，b]上的量

2、所求量对区间有可加性

方法

找积分范围
找微元
求积分

一、平面图形的面积

求曲线所围面积① $y^2 = x,y =x^2$

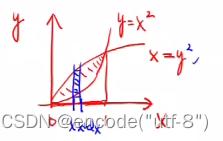
找到积分范围 [0，1]
微元：dx宽度下，对应的面积为多少（此时面积近似为矩形，上底为上曲线的函数值，下底为下曲线的函数值，得到高为二者的差值）——也就是根号x - x平方
得到积分公式： $\int_{0}^{1}\sqrt{x}-x^2dx$

同理，将y看作积分变量也可以得到同样的结果

求曲线所围面积② $y^2 = 2x,y =x-4$

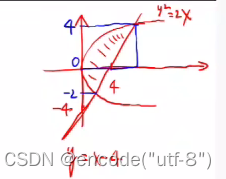
找到积分范围[0，8]
找微元：此时x=4左右两边情况不一样，需要分段讨论，积分也要分段求
列出积分求解： $S= \int_{0}^{2}2\sqrt{2x}dx+\int_{2}^{8}(\sqrt{2x}-(x-4))dx$

这题用y作为变量更加容易列式，且积分不需要分段

求曲线所围面积③ $x = a(t-sint),y = a(1-cost),0\leq t\leq 2\pi$

求与x轴所围面积

范围 [0，2πa]
找微元：此时矩形的高为 y = f(t)，而矩形的宽为dx，
- 要么把y写成只关于x的形式，那么需要通过x的表达式解出t，但显然很复杂
- 要么把dx写成dt的式子：由Udt = Udx * Xdt
得到积分式子： $S = \int_{0}^{2\pi a}y(x)dx = \int _{0}^{2\pi}a(1-cost) x'dt = \int _{0}^{2\pi}a(1-cost)a(1-cost)dt$

求曲线所围面积④

求心形线 $\rho = a(1+cos\theta )(a>0)$ 所围面积

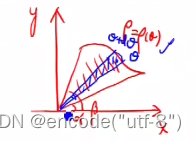
极坐标问题一般取θ作为变量，那么范围就是 [0，2π]
找微元：此时需要算的就是小扇形的面积，扇形的母线长度都看作 ρ（θ）
写出积分式求解： $S = \int_{0}^{2\pi}\frac{1}{2}\rho^2 (\theta)d\theta$

二、体积

1.旋转体的体积

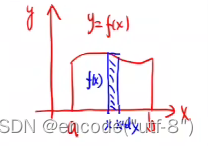
绕x轴转：取宽度dx的部分进行旋转，得到的其实是一个高为dx，底面半径为 f(x)的圆柱

体积的表示直接代入圆柱体积公式

$V = \pi \int_{a}^{b}f^2(x)dx$

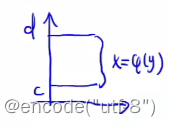
绕y轴转：取宽度dy的部分进行旋转，得到的其实是一个高为dy，底面半径为 φ(y)的圆柱

体积的表示直接代入圆柱体积公式

$V = \pi\int_{c}^{d}\varphi ^2(y)dy$

注意：但一般给出形式仍然是 y = f(x)，此时需要改变公式的推导过程

取宽度dx的带状区域绕y轴旋转，得到的是类似一个长方体的立体区域

其中底面长为 2πx，底面宽为dx，高为 f (x)，根据长方体体积，得到积分公式

$V = 2\pi\int_{a}^{b}xf(x)dx$

2.平行截面积已知的立体的体积

由于截面积已知，对于每个dx都可以看成求一个柱体的体积，也就是dv = S(x)dx

$V = \int_{a}^{b}S(x)dx$

试求椭球体体积： $\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$

提示：此处选取一个变量固定时（比如选取y），那么当y = y时，得到的其实是一个x-z平面的截面，而它为椭圆，此时利用椭圆面积公式πab即可列出积分公式

$V = \int_{-b}^{b}\pi ab(1-\frac{y^2}{b^2})dy$

3.平面曲线的弧长

推导弧长的公式（y = f(x)型 ）：取得dx，要得到这一点的长度，应该是在dx长度内构建一个直角三角形，

那样就有 $(dl)^2 = (dx)^2+(dy)^2$ ， $dl = \sqrt{(dx)^2+(dy)^2}$

又因为 $f'(x) = \frac{dy}{dx}$ ，所以化简得到 $L = \int \sqrt{1+f'(x)}dx$

（参数方程型）：同样根据 $dl = \sqrt{(dx)^2+(dy)^2}$ ，

直接根据关系，直接代入dx与dy： $dx = \varphi '(t)dt,dy = \psi '(t)dt$

$L = \int \sqrt{\varphi '(t)+\psi '(t)}dt$

（极坐标型）：同样根据 $dl = \sqrt{(dx)^2+(dy)^2}$ ，但此时dx，dy，dθ的关系要注意ρ(θ)

$dx = d(\rho (\theta )cos\theta ) =( \rho '(\theta )cos\theta -\rho (\theta )sin\theta ) d\theta$

$dy = d(\rho (\theta )sin\theta ) = (\rho '(\theta )sin\theta +\rho (\theta )cos\theta )d\theta$

$(dx)^2+(dy)^2 = \rho (\theta )+ \rho' (\theta )$

然后就得到了最终的弧长公式： $L = \int \sqrt{\rho^2(\theta )+\rho'^2 (\theta )}d\theta$

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。