梯度下降算法

简介

梯度下降是用来最小化成本函数的一个算法。
比如一个线性模型函数是f(x) = wx +b，w和b是常量参数，我们要做的是每次都稍微改变参数w和b，以尝试降低w和b的成本J，最终让成本函数j的值稳定或者无限接近于最小值，保证该模型的拟合直线近于完美。

梯度算法原理

如下图是一个某神经网络的成本函数J的三维立体图形，给定的常量参数起始值是小人的当前位置，梯度算法的目标是为了让图中的小人找到这个立体图形的最低谷。编码角度来讲这应该属于一个贪心算法，每走一步的都要思考下一步如何走可以最快走到谷底

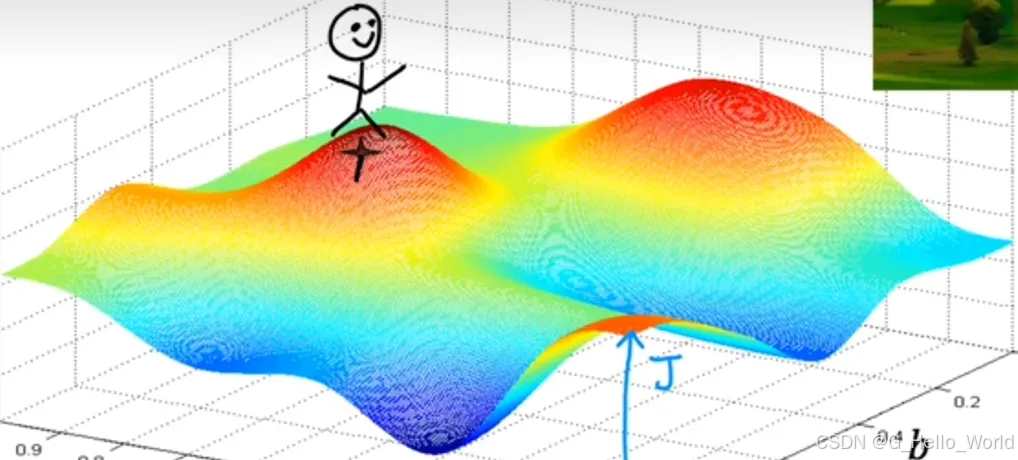
小人的最终路径如下图 红色箭头 所示

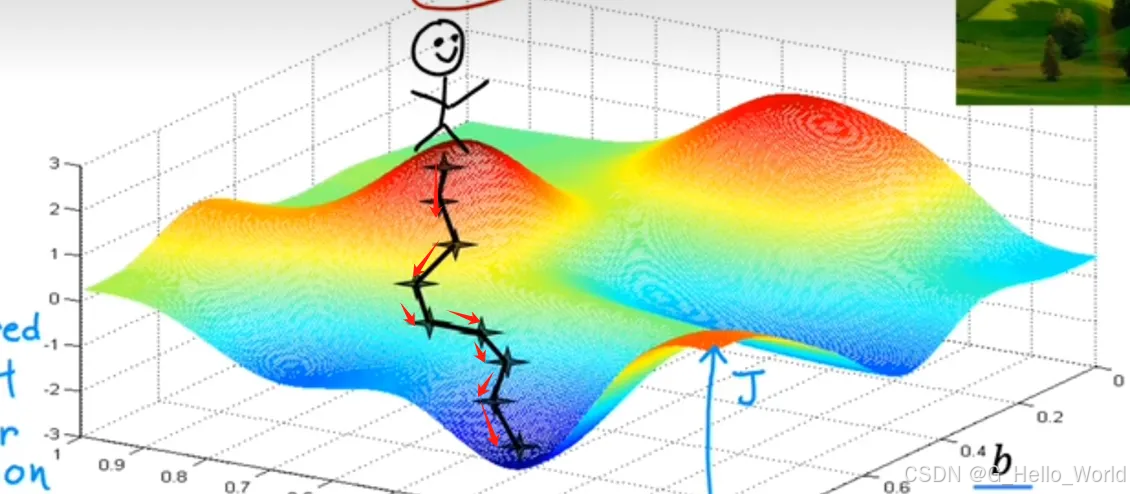
局部极小值

上述原理中提到了一个比较有趣的点，小人的起始位置是根据我们自定义的常量参数值计算出来的，基于那个位置得到的是左下角的山谷；如果小人的位置在下图中的位置，得到的结果就是这个样子；其实这并不是对错之分，这是算法的特性，这两个山谷称为局部极小值，在我们实际使用过程中可能会有N个局部极小值

梯度算法实现

每次下降梯度，都会计算出新的常量参数w和b，梯度下降算法公式如下
$w(新)=w（旧）-\alpha （学习率）\times \frac{\partial }{\partial w}J(w,b)（成本函数J的导数项）$
$b(新)=b（旧）-\alpha （学习率）\times \frac{\partial }{\partial b}J(w,b)（成本函数J的导数项）$
学习率（α）：通常指0到1的随机小正数，可以是0.01也可以是0.02等等，是用来控制我们向下走的步幅的，这个步幅可能会导致我们下落到的局部极小值不同
PS：这里的求导过程中，w和b都是用的原始值，不应用某一新值，所以在编码实现的时候要注意引用赋值