博弈搜索
博弈问题形式化
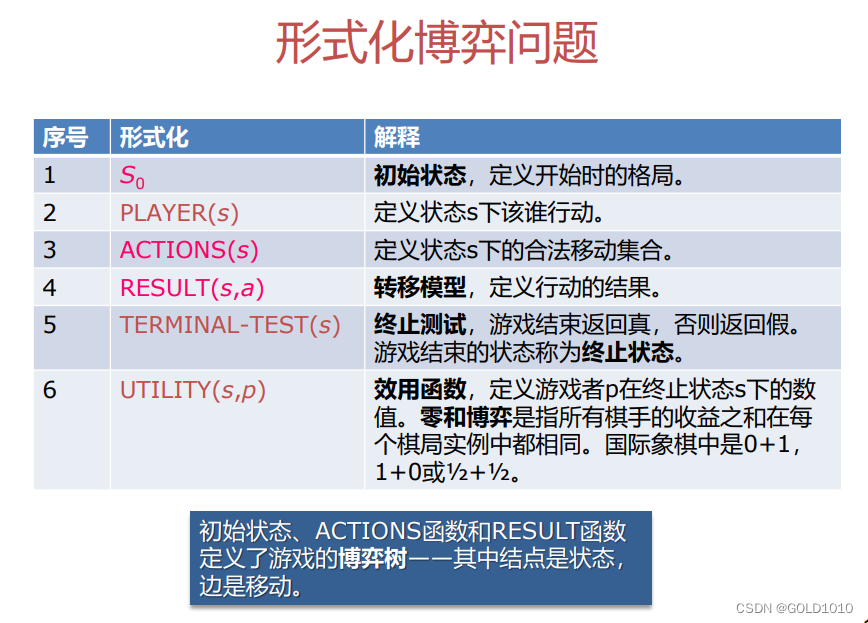

博弈中的优化决策
minimax算法



minmax算法,其基本思想是,由于该决策具有先手顺序,因此先手玩家想要自己的利益最大化,而后手玩家想要让先手玩家利益最小化。因此A结点使用max,而B,C,D结点使用min
多人博弈时的最优决策
多人博弈的最优决策与上面的决策类似,我们每个结点都用一个向量来表示,每次选择每个人都会去选择让自己利益最大化的状态。

以上图为例
A会选择(3,2,6),因为(3,2,6)>(1,2,6)
B会选择(3,2,6),因为(3,2,6)>(4,1,7)
C会选择(3,2,6),因为(3,2,6)>(2,3,4)

α-β剪枝和行棋排序
α-β剪枝的思路来源于MiniMax算法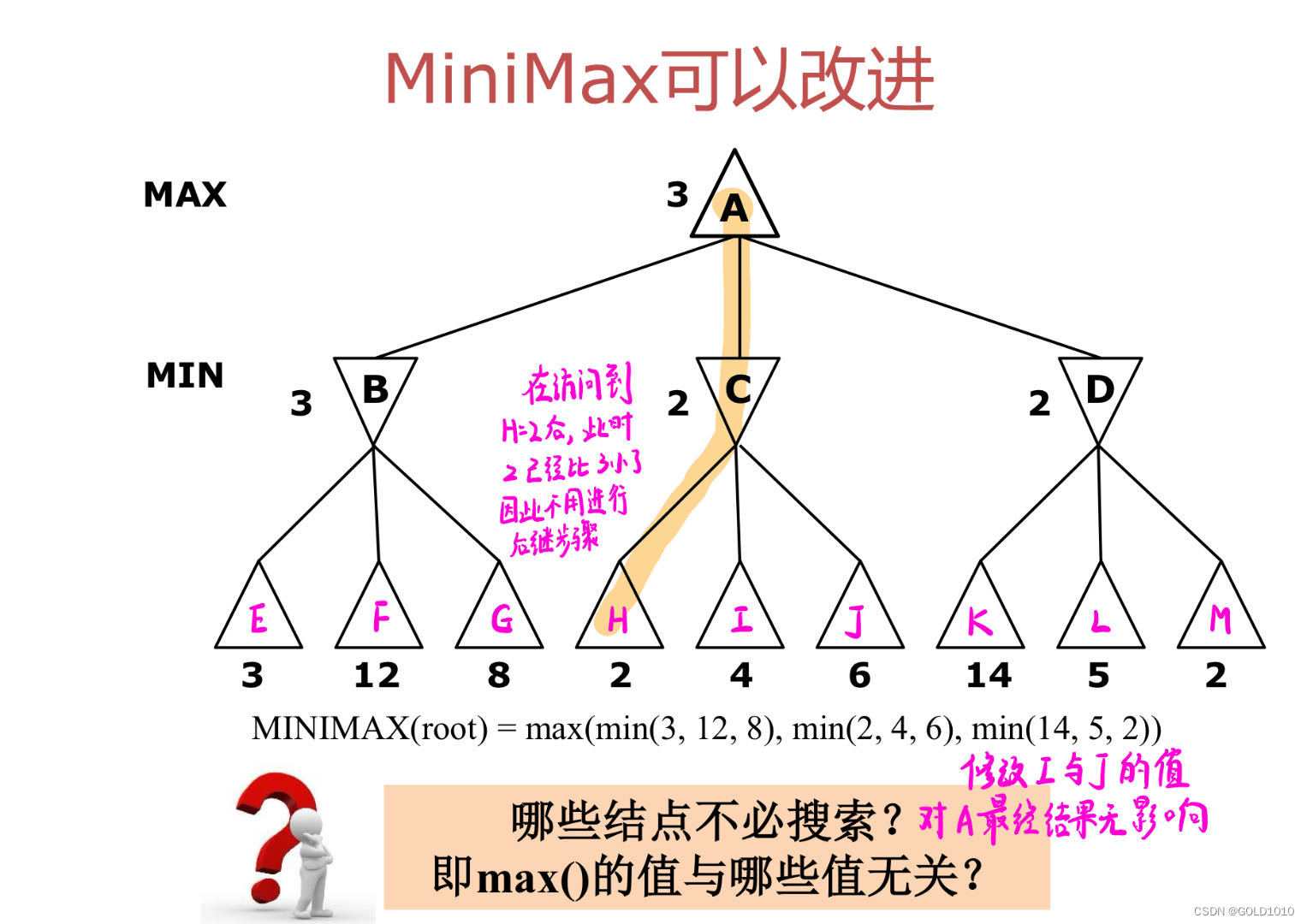
当访问最左边那条子树之后,返回给MAX=3
当我们接着访问中间这条子树,当访问到H=2时,此时已经可以不用再访问I和J了
因为I和J不论取什么值,都不会更改MAX的取值
我们可以利用下图分析整个搜索过程中,结点取值的范围


以这张图为例
先访问E结点,故B的最大值目前为3
再访问F结点,但F结点比E结点大,因此不会影响B的取值,B的最大值目前仍然为3
再访问G结点,与上同理,B的最大值目前仍然为3
左边子树访问结束,因此B的取值就是3
将B的取值传回A中,因此A的最小值为3
访问中间子树
访问H结点,取值为2,因此C的最大值为2
此时无需访问J和K结点,因为J和K的取值为A无影响
将C的值传回A,由于A最小值为3,因此C的值对A不发生改变
访问右边子树
访问L结点,取值为14,因此D的最大值为14
访问M结点,取值为5,因此D的最大值改为5
访问N结点,取值为2,因此D的最大值改为2
将D的值传回A,由于A最小值为3,因此D的值对A不发生改变









可以这么理解,此时A结点的范围是[3,+∞],因此对于A而言,它想要在下面找到比三大的数,由于你此时返回给C的是个比3小的数,因此不符合要求,那么该子树其他节点也不需要看了
对于D结点而言,首先返回的是14 ,是个比3大的数,因此说明有希望,继续往下搜索
又找到了5,也是个比3大的数,因此说明有希望,继续再往下搜搜
找到了2,是个比3小的数,那么这颗子树所有的搜索过程都白费了,因为出现了一个我们不想要的数
通过上述过程,我们可以发现,每个子树结点的先后顺序也很重要
在上述过程中,我们在搜索右边子树的过程中,如果一开始就发现了2这个值,我们压根就不需要继续搜索两个分支。

总结:
对于min节点的子节点:由小到大排序有助于剪枝
对于max节点的子节点:由大到小排序有助于剪枝
不完美的实时决策
完美决策:不考虑决策的时间和空间
不完美决策:考虑决策的时间和空间,由于状态空间巨大,因此有限时间内只能考虑很小的一部分
因此,我们需要在给定的有限时间内做决策,需要尽早截断搜索,不一定要等到终止状态才能评估和回传结果。
由于效用函数是必须要到叶节点才能使用,因此我们需要使用启发式评估函数EVAL来取代效用函数Utility,而用截断测试来取代终止测试。
以井字棋为例进行说明

我们以开放给X的位置和开放给O的位置的差作为EVAL的值
以绿色作为MAX,黄色作为MIN。
此时限制深度为2,因此可以由MINIMAX算法得出,MAX的值为1,即右边子树作为移动方向
但对于MIN而言,他不一定会选择执行1,而有可能执行2。
因为对于MIN而言,它也需要搜索两次,此时的1和2都只是第一层,因此不能将此处1和2作为MIN决策依据。
我们不妨假设MIN选择了2,则有下面这个图(因为2和下面的1是对称的,两者相同)

由上图可知从MAX 出发,搜索两层的图如上所示
如何截断,从而来满足时间上的限制呢?
截断的方法:
①设置固定深度
②迭代加深


随机博弈
即每个结点都以一定概率选择子节点
此处一般直接取期望值作为当前结点的值





















 1551
1551

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








