统计学习及监督学习概论
书目录
统计学习
统计学习分类基本分类(监督、无监督、强化、半监督)
按模型分类(概率和非概率、线性和非线性、参数化和非参数化)
按算法分类(在线、batch)
按技巧分类(贝叶斯、核方法)统计学习三要素
模型、算法、策略
模型评估与模型选择
误差
过拟合
模型选择方法正则化和交叉验证
生成模型和判别模型
监督学习应用
1、统计学习
Steps:
得到一个有限的训练数据集合
确定包含所有可能的模型的假设空间,即学习模型的集合
确定模型选择的准则,即学习的策略
实现求解最优模型的算法,即学习的算法
通过学习方法选择最优的模型
利用学习的最优模型对新数据进行预测或分析
2、统计学习分类
2.1 基本分类
监督学习
学习输入到输入的映射的统计规律
基本假设:输入变量 XXX 和输出变量 YYY 遵循联合概率分布P(X,Y)P(X,Y)P(X,Y)
假设空间:由输入空间到输出空间的映射的集合
学习过程:训练+预测
\quad 给定训练集T=(x1,y1),(x2,y2),……,(xn,yn)T={(x_{1},y_{1}),(x_{2},y_{2}),……,(x_{n},y_{n})}T=(x1,y1),(x2,y2),……,(xn,yn)
\quad 首先通过学习训练集得到一个模型,表示为条件概率分布P^(Y∣X)\hat{P}(Y|X)P^(Y∣X)或决策函数Y=f^(X)Y=\hat{f}(X)Y=f^(X)
\quad 对于给定的测试样本集中的输入xn+1x_{n+1}xn+1,由模型argmaxP^(Y∣Xn+1)argmax\hat{P}(Y|X_{n+1})argmaxP^(Y∣Xn+1)或决策函数Y=f^(Xn+1)Y=\hat{f}(X_{n+1})Y=f^(Xn+1)给出输出yn+1y_{n+1}yn+1
模型方法:
- 生成方法:
– 由数据学习联合概率分布P(X,Y)P(X,Y)P(X,Y),在此基础上求P(Y∣X)P(Y|X)P(Y∣X),即P(Y∣X)=P(X,Y)P(X)P(Y|X)=\dfrac{P(X,Y)}{P(X)}P(Y∣X)=P(X)P(X,Y)
– 收敛速度快, 当样本容量增加时, 学到的模型可以更快收敛到真实模型
– 当存在隐变量时仍可以用 - 判别方法:
– 直接学习P(Y∣X)P(Y|X)P(Y∣X),无法还原P(X,Y)P(X,Y)P(X,Y)
– 直接面对预测, 往往学习准确率更高
– 可以对数据进行各种程度的抽象, 定义特征并使用特征, 可以简化学习问题
应用:
- 分类问题:输出变量Y是离散变量,一般有二分类和多分类问题。
- 标注问题:输出一个输入序列的标记序列
- 回归问题
非监督学习
从无标注数据中学习预测模型的机器学习问题,本质是学习数据中的统计规律或潜在结构。
与监督学习相比,无监督学习的输出空间ZZZ 是一个隐式结构空间
强化学习 | 半监督学习和主动学习
暂时略过
2.2按模型分类
- 概率模型
–条件概率分布形式P(Y∣X)P(Y|X)P(Y∣X)【可以转化为函数 形式Y=f(X)Y=f(X)Y=f(X)】 - 非概率模型形式:
–函数形式Y=f(X)Y=f(X)Y=f(X)【联合概率分布不一定存在】
***在监督学习中,概率模型是生成模型,非概率模型是判别模型。
2.3按算法分类
2.4按技巧分类
贝叶斯方法:后验概率最大化
核方法
3、三要素
3.1模型
| 假设空间 | |
|---|---|
| 条件概率分布 | F={P∣Y=Pθ(Y∣X),θ∈Rn}F=\{P\vert Y=P_{\theta}(Y\vert X),\theta\in\R^{n}\}F={P∣Y=Pθ(Y∣X),θ∈Rn} |
| 决策函数 | F={f∣Y=fθ(X),θ∈Rn}F=\{f\vert Y=f_{\theta}(X),\theta\in\R^{n}\}F={f∣Y=fθ(X),θ∈Rn} |
3.2策略
度量函数
损失函数【度量模型一次预测的好坏】
\quad是关于预测值f(X)和真实值Y的非负实值函数,记作L(Y,f(X))L(Y,f(X))L(Y,f(X))
\quad损失函数越小,模型效果越好
- 0-1损失函数
L(Y,f(X))={1,Y≠f(X)0,Y=f(X)L(Y,f(X))=\begin{cases} 1, & Y \not = f(X) \\ 0, &Y=f(X) \end{cases}L(Y,f(X))={1,0,Y=f(X)Y=f(X) - 平方损失函数
L(Y,f(X))=(Y−f(X))2L(Y,f(X))=(Y-f(X))^2L(Y,f(X))=(Y−f(X))2 - 绝对损失函数
L(Y,f(X))=∣Y−f(X)∣L(Y,f(X))=|Y-f(X)|L(Y,f(X))=∣Y−f(X)∣ - 对数损失函数
L(Y,f(X))=−log(Y−f(X))L(Y,f(X))=-log(Y-f(X))L(Y,f(X))=−log(Y−f(X))
风险函数【损失函数的期望,度量平均意义下模型预测的好坏】
\quad和模型的泛化误差的形式一样,是模型f(X)f(X)f(X)关于联合分布P(X,Y)P(X,Y)P(X,Y)的平均意义下的损失(期望损失),但由于P(X,Y)P(X,Y)P(X,Y)是未知的,所以不能直接计算
Rexp(f)=Ep[L(Y,f(X)]=∫χ×γL(y,f(x))P(x,y)dxdyR_{exp}(f)=E_{p}[L(Y,f(X)]=\int_{\chi\times\gamma}L(y,f(x))P(x,y)dxdyRexp(f)=Ep[L(Y,f(X)]=∫χ×γL(y,f(x))P(x,y)dxdy
经验风险
\quad模型f(X)f(X)f(X)关于训练样本集的平均损失。根据大数定律,当样本容量N趋于无穷大时,经验风险趋于期望风险
Remp(f)=1N∑i=1NL(yi,f(xi))R_{emp}(f)=\dfrac{1}{N}\sum_{i=1}^NL(y_{i},f(x_{i}))Remp(f)=N1∑i=1NL(yi,f(xi))
风险最小化
- 经验风险最小化ERM
minf∈F1N∑i=1NL(yi,f(xi)min_{f\in F} \dfrac{1}{N}\sum_{i=1}^NL(y_{i},f(x_{i})minf∈FN1∑i=1NL(yi,f(xi) - 结构风险最小化SRM【防止过拟合,等价于正则化】
Rsrm(f)=1N∑i=1NL(yi,f(xi)+λJ(f)R_{srm}(f)=\dfrac{1}{N}\sum_{i=1}^NL(y_{i},f(x_{i})+\lambda J(f)Rsrm(f)=N1∑i=1NL(yi,f(xi)+λJ(f)
其中J(f)J(f)J(f)为模型复杂度;λ≥0\lambda \ge0λ≥0是系数
使经验风险和模型复杂度同时小,后者是因为奥卡姆剃刀原则
minf∈F1N∑i=1NL(yi,f(xi)+λJ(f)min_{f\in F} \dfrac{1}{N}\sum_{i=1}^NL(y_{i},f(x_{i})+\lambda J(f)minf∈FN1∑i=1NL(yi,f(xi)+λJ(f)
3.3算法
4、训练误差和模型选择(泛化能力、过拟合)
4.1训练误差与测试误差
训练集和测试集上的经验风险
4.2泛化能力
- 泛化误差(风险函数)
Rexp(f)=Ep[L(Y,f(X)]=∫χ×γL(y,f(x))P(x,y)dxdyR_{exp}(f)=E_{p}[L(Y,f(X)]=\int_{\chi\times\gamma}L(y,f(x))P(x,y)dxdyRexp(f)=Ep[L(Y,f(X)]=∫χ×γL(y,f(x))P(x,y)dxdy - 泛化误差上界
学习方法的泛化能力往往是通过研究泛化误差的概率上界进行的,泛化误差上界是样本容量的函数,当样本容量增加时趋于0;也是假设空间的函数,假设空间容量越大,模型越难学,泛化误差上界越大。
二分类问题的泛化误差上界
4.3性能度量*
acc=1N∑i=1NI(yi=f^(xi))acc=\dfrac{1}{N}\sum_{i=1}^NI(y_{i}=\hat f (x_{i}))acc=N1∑i=1NI(yi=f^(xi))
二分类问题:
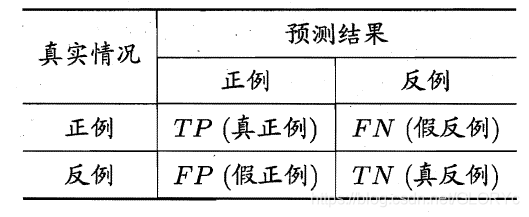
-
精确率Precision P=TPTP+FPP=\dfrac{TP}{TP+FP}P=TP+FPTP
-
召回率Recall R=TPTP+FNR=\dfrac{TP}{TP+FN}R=TP+FNTP
-
F1值2F1=1P+1R\dfrac{2}{F_{1}}=\dfrac{1}{P}+\dfrac{1}{R}F12=P1+R1
-
P-R曲线:以Precision为纵轴、Recall为横轴作图,曲线与y=x的交点称为平衡点
-
FβF_{\beta}Fβ:F1的一般形式,Fβ=(1+β2)×P×Rβ2×P+RF_{\beta}=\dfrac{(1+\beta^2) \times P \times R}{\beta^2 \times P +R}Fβ=β2×P+R(1+β2)×P×R,其中β\betaβ度量了Recall对Precision的相对重要性【β\betaβ如何确定?】
-
ROC:以TPR为纵轴,FPR为横轴作图
TPR(真阳性率)=TPTP+FN\quad TPR(真阳性率)=\dfrac{TP}{TP+FN}TPR(真阳性率)=TP+FNTP
TPR(假阳性率)=FPFP+TN\quad TPR(假阳性率)=\dfrac{FP}{FP+TN}TPR(假阳性率)=FP+TNFP -
AUC :ROC曲线下的面积
4.4过拟合
学习时选择的模型所包含的参数过多,导致模型对已知数据预测得很好,对未知数据预测得很差。
正则化:等价于结构风险最小化
minf∈F1N∑i=1NL(yi,f(xi)+λJ(f)\quad \quad min_{f\in F} \dfrac{1}{N}\sum_{i=1}^NL(y_{i},f(x_{i})+\lambda J(f)minf∈FN1∑i=1NL(yi,f(xi)+λJ(f)
L1正则化: L1范数∑i=1N∣ωi∣L1范数\sum_{i=1}^N|\omega_{i}|L1范数∑i=1N∣ωi∣
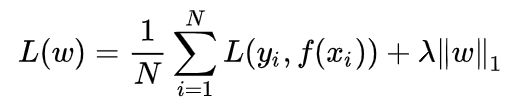
L2正则化:L2范数∑i=1Nωi2L2范数\sqrt{\sum_{i=1}^N\omega_{i}^2}L2范数∑i=1Nωi2
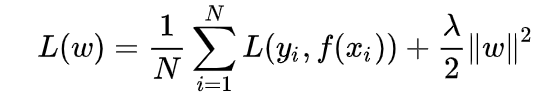
- L1正则化:模型参数ω\omegaω先验分布服从零均值拉普拉斯分布,此时:L(ω)=P(Y∣ω)P(ω)L(\omega)=P(Y|\omega)P(\omega)L(ω)=P(Y∣ω)P(ω),即对数似然函数中增加了负的ω\omegaωL1范数,即相应的损失函数中增加了L1正则项
- L2正则化:模型参数ω\omegaω先验分布服从零均值高斯分布,此时:L(ω)=P(Y∣ω)P(ω)L(\omega)=P(Y|\omega)P(\omega)L(ω)=P(Y∣ω)P(ω),即对数似然函数中增加了负的ω\omegaωL2范数,,即相应的损失函数中增加了L2正则项
交叉验证
基本思想:重复地使用数据,把给定的数据进行切分,将切分的数据集组合为训练集与测试集,在此基础上反复地进行训练、测试以及模型选择。
- 简单交叉验证(留出法):直接划分好训练数据和测试数据,在训练数据上做训练,测试数据上做测试
- k折交叉验证 (k-folds):首先随机地将已给数据切分为k个互不相交、大小相同的子集;然后利用k-1个子集的数据训练模型,利用余下的子集测试模型;将这一过程对可能的k种选择重复进行;最后选出S次评测中平均测试误差最小的模型。
- 留一法(leave one out):k折交叉验证的特殊情形,k=N。适用于N较小的情况。
此外模型评估方法还有Bootstrap(自助法),从样本中进行重抽样构型子样本,由子样本估计样本再估计总体,仅适用于小样本





 本文介绍了统计学习的基本概念,包括监督学习、非监督学习等不同学习方式,并探讨了模型选择、正则化等关键主题。
本文介绍了统计学习的基本概念,包括监督学习、非监督学习等不同学习方式,并探讨了模型选择、正则化等关键主题。
















 418
418










