二叉树（1）

 十分抱歉，停更了差不多一个月。暑假了，我又回来了！

概念

节点的度

叶子节点或终端节点：度为0的节点称为该节点的度

非终端节点或分支节点：度不为0的节点

双亲节点或父节点：若一个节点含有子节点，则称该节点为其子节点的父节点

孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点

兄弟节点：具有相同父节点的子节点称为兄弟节点

树的度：一棵树的最大节点数称为树的度

节点的层次：从根开始定义，根为第一层，根的子节点为第2层‘’

树的高度或深度：树中节点的最大层次

堂兄弟节点：双亲在同一层的节点互为堂兄弟

节点的祖先：从根到该节点所经分支上的所以节点

森林：由m棵互不相交的树的集合。

/*#define N 4
struct TreeNode
{
   int val;
   struct TreeNode* subs[N];
};明确树的度是4*/
//如果没有明确树的度是4
//如果没有明确树的度
/*struct TreeNode
{
   int val;
   SeqList subs;//顺序表内部存struct TreeNode*
 };*/
 //左孩子 右兄弟表示法
struct TreeNode
{
   int val;
   struct TreeNode*leftchild;
   struct TreeNode*rightBrother;
};

代码 

typedef int BTDataType;
typedef struct BinaryTreeNode
{
   BTDataType data;
   struct BinaryTreeNode* left;
   struct BinaryTreeNode* right;
}BTNode;
BTNode* BuyNode(int x)
{
   BuyNode* node=（BTNode*）malloc(sizeof(BTNode));
   if(node==NULL)
   {
      perror("malloc fail");
      return NULL;
   }
   node->data=x;
   node->left=NULL;
   node->right=NULL;
}


BTNode* CreatBinaryTree()
{
   BTNode* node1=BuyNode(1);
   BTNode* node1=BuyNode(2);
   BTNode* node1=BuyNode(3);
   BTNode* node1=BuyNode(4);
   BTNode* node1=BuyNode(5);
   BTNode* node1=BuyNode(6);
   node1->left=node2;
   node1->right=node4;
   node2->left=node3;
   node4->left=node5;
   node4->right=node6;  
   return node1;
}
void PrevOrder(BTNode* root)
{
  if(root==NULL)
  {
     printf("N\n");
     return;
   }
  printf("%d ",root->data);
  PrevOrder(root->left);
  PrevOrde(root->right);
}
int main()
{
   BTNode* root=CreatBinaryTree();
   PrevOrder(root);
   printf("\n");
   return 0;
}

接下来，我们来看看这个代码的执行过程。

首先，根节点1不为空，打印根节点1，打印完1之后访问1的左子树和右子树。递归调用左子树和右子树，建立新的栈帧。再接着把1的左传过来，打印2，打印完2，再递归调用2的左，也就是3。再打印3的左子树，左子树是一个空，就调用return，是回到调用的地方，也就是回到3，接着调用3的右边，3的右边又是一个空。打印一个空，又回到调用的地方。3的左边调用占用的空间和3的右边调用占用的空间是同一块空间。（空间不用，给下一个人）递归调用就是一份指令，只不过是一份指令执行多次的过程当中，传的参数不同，执行逻辑就不同。参数是存在栈帧里面的。当前函数当中的东西出了作用域就销毁了，函数调用结束，栈帧销毁，东西就跟着销毁了。全局变量不存在栈帧，存在一个单独的区域。（生命周期是全局）那么，malloc出的为什么不会销毁呢？malloc是要就会分配，不要了释放，才归还给它。

那么，中序遍历的代码怎么写呢？

void InOrder(BTNode* root)
{
  if(root==NULL)
  {
     printf("N\n");
     return;
   }
  InOrder(root->left);
  printf("%d ",root->data);
  InOrder(root->right);
}

如果要求节点的个数，应该怎么求呢？

int TreeSize(BTNode* root)
{
      static int size=0;
      if(root==NULL)
        return 0;
      else
        ++size;
      TreeSize(root->left);
      TreeSize(root->right);
      return size;
}
int TreeLeafSize(BTNode* root)
{
int TreeHeight(BTNode* root)
{

如果size用static修饰，那么他就存在静态区里，不存在栈帧里。第二次调用，size不会被初始化为0，而是进行累加。

int TreeSize(BTNode* root,int* psize)
{
      if(root==NULL)
        return 0;
      else
        ++(*psize);
      TreeSize(root->left,psize);
      TreeSize(root->right,psize);
      return *psize;
}
int main()
{
     BTNode* root=CreatBinarytree();
     

每个栈帧里都有一个指针，但是这个指针是指向同一个的。

更好的思路是用分支递归的思路来写：

1、节点为空，个数就是0个

2、节点不为空，分成左子树节点+自己（1）+右子树节点--认为走了一个后序

int TreeSize(BTNode* root)
{
   return root==NULL?0:TreeSize(root->left)+TreeSize(root->right)+1;
}

统计叶子结点（如果不是叶子结点，就等于左节点加右节点）

int TreeLeafSize(BTNode* root)
{
   if(root==NULL)
     return 0;
   if(root->left==NULL&&root->right==NULL)
     return 1;
   return TreeLeafSize(root->left)+TreeLeafSize(root->right);
}

这个代码，如果是空树，就会存在问题。即使不是空树，遇到度为1，出现空指针。因为&&是两边的表达式都为真，才会进入这个分支，那么你一边为空，另一边不是，那么下一层就是传入的空指针，就会解引用空指针的。

求高度

空树的高度：0

假设我已经知道左右子树的高度，那么我的高度等于多少呢？等于较大的那个数加上1。

int TreeHeight(BTNode* root)
{
   if(root==NULL)
     return 0;
   int leftHeight=TreeHeight(root->left);
   int rightHeight=TreeHeight(root->right);
   return leftHeight>rightHeight?leftHeight+1:rightHeight+1;
}

如果不统计，就会重复计算多次。

那如果代码是这样，还会重复计算吗？

int fmax(int x,int y)
{
   return x>y?x:y;
}
int TreeHeight(BTNode* root)
{
   if(root==NULL)
     return 0;
   return fmax(TreeHeight(root->left),TreeHeight(root->right))+1;
]

树的高度

如果为空，就是0，如果不为空，且k=1，那么返回1，如果k大于1，那么等于左子树的k-1层＋右子树的k-1层

二叉树第k层节点个数

int TreeLevelKSize(BTNode* root,int k)
{
    if(root==NULL)
     return 0;
    if(k==1)
    {
       return 1;
    }
    return TreeLevelKSize(root->right,k-1)+TreeLevelKSize(root->left,k-1);
}

二叉树找出节点为x的数

这道题返回的是节点的指针：容易出错

接下来，我们将分析一些错误代码，一一解读他们的问题。

1

BTNode* BinaryTreeFind(BTNode* root,BTDataType x)
{
  if(root==NULL)
    return NULL;
  if(root->data==x)
    return root;
  BinaryTreeFind(root->left,x);
  BinaryTreeFind(root->right,x);
}

第一个问题是，如果没有进if，就没有返回值。

第二个问题是，如果要查找3，那么我们从第一个节点开始走。1是不是3，不是3，那么往下递归，当前不是3，往左子树递归，当前不是3，往左子树递归，最后找到3，返回上一层，并不是返回3。

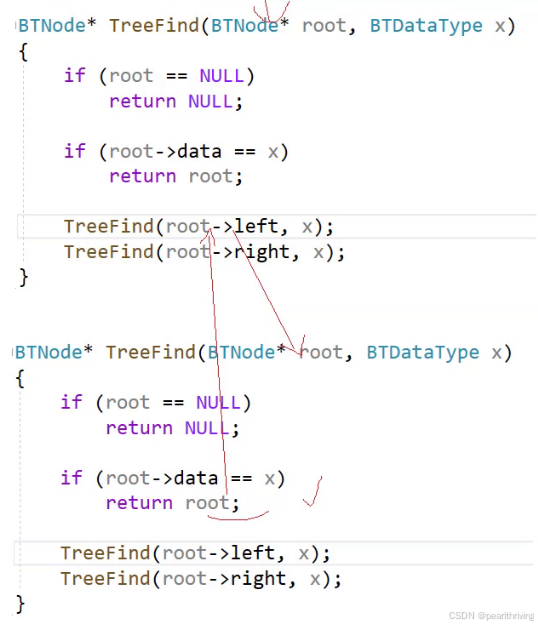
找到之后，回退到上一层左子树，没有。继续找该层的右子树，没有找到。

那么这一题的正确写法是什么呢？

BTNode* BinaryTreeFind(BTNode* root,BTDataType x)
{
  if(root==NULL)
    return NULL;
  if(root->data==x)
    return root;
  BTNode*ret1=BinaryTreeFind(root->left,x);
  if(ret1)
    return ret1;
  BTNode*ret2=BinaryTreeFind(root->right,x);
  if(ret2)
    return ret2;
  return NULL;
}

接下来，我们来看另一种写法：

BTNode* BinaryTreeFind(BTNode* root,BTDataType x)
{
   if(root==NULL)
      return NULL;
   if(root->data==x)
      return root;
   BTNode*ret=BinaryTreeFind(root->left,x);
   if(ret1)
      return ret1;
   return BinaryTreeFind(root->right,x);
   }

单值二叉树

. - 力扣（LeetCode）

bool isUnivalTree(struct TreeNode* root) {
    if(root==NULL)
    return true;
    if(root->left&&root->left->val!=root->val)
    {
        return false;
    }
    if(root->right&&root->right->val!=root->val)
    {
        return false;
    }
    return isUnivalTree(root->left)&&isUnivalTree(root->right);
}

如果一直和一个值比较：

bool _isUnivalTree(struct TreeNode* root,int val)
{
  
}
bool isUnivalTree(struct TreeNode* root)
{
  
}

相同的树

100. 相同的树 - 力扣（LeetCode）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
    if(p==NULL&&q==NULL)
    {
        return true;
    }
    if(p==NULL||q==NULL)//一个为空，一个不为空的情况（如果有一个为空，已经在上面return了）
    {
        return false;
    }
    if(p->val!=q->val)
    {
        return false;
    }
    return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);l;

}

对称二叉树

. - 力扣（LeetCode）

跟和跟比较，左子树和右子树比较。

二叉树的前序遍历

int TreeSize(struct TreeNode* root)//统计节点的个数
 {
    return root==NULL?0:TreeSize(root->left)+TreeSize(root->right)+1;
 }
 void preOrder(struct TreeNode* root,int* a,int* pi)
 {
    if(root==NULL)
    return;
    a[i++]=root->val;
    preOrder(root->left,a,i);
    preOrder(root->right,a,i);
 }
 //遍历一遍，将这棵树节点的个数求出来
int* preorderTraversal(struct TreeNode* root, int* returnSize) {
    *returnSize=TreeSize(root);//输出型参数
    int*a=(int*)malloc(sizeof(int)*(*returnSize));
    int i=0;
    preOrder(root,a,&i);
    return a;

}

我们期望右边的i是2，但是问题是右边的i是1，这是为什么呢？主要是因为左边形参的改变不会影响左边实参的变化，右边的i是在原有的0上加1。

那么这个问题应该怎么解决呢？

数组 a：这是一个用于存储二叉树节点值的数组。

如果你直接传递一个整数索引，函数内部对该索引的任何修改都不会影响到函数外部的那个变量。但是，如果你传递一个指向该整数的指针，那么函数内部就可以通过解引用这个指针来修改原始变量。

使用指针而不是直接返回整数的原因是：

1. 多个返回值：C语言函数只能返回一个值，但通过指针参数，你可以“返回”多个值。
2. 修改外部变量：通过指针，你可以在函数内部修改函数外部定义的变量的值。这在某些情况下是非常有用的，比如当你需要更新一个状态或配置时。
3. 效率：避免不必要的内存分配和复制。如果你只是传递一个整数的值而不是它的地址，那么每次函数返回时都需要复制这个值。而使用指针则可以直接修改原始内存位置的值，避免了这种复制。
4. 灵活性：使用指针可以让你传递任何类型的数据，而不仅仅是基本数据类型。你可以传递一个指向任何数据结构（如数组、结构体、联合体等）的指针，并在函数内部修改这个数据结构的内容。

另一棵树的子树

572. 另一棵树的子树 - 力扣（LeetCode）

找出root所有子树，跟subroot比较。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
    if (p == NULL && q == NULL) {
        return true;
    }
    if (p == NULL ||
        q == NULL) // 一个为空，一个不为空的情况（如果有一个为空，已经在上面return了）
    {
        return false;
    }
    if (p->val != q->val) {
        return false;
    }
    return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) {
    if (root == NULL) {
        return false;
    }
    if (root->val == subRoot->val && isSameTree(root, subRoot))
        return true;

    return isSubtree(root->left, subRoot) ||isSubtree(root->right, subRoot);
}

具体的比较过程如下： 

1. 检查根节点：
   • root不为空，进入下一层判断。
   • root->val（值为1）不等于subRoot->val（值为2），所以root不是与subRoot相同的树。
2. 递归检查左子树：
   • 调用isSubtree(root->left, subRoot)，注意：只有当左子树不满足条件时，才会检查右子树，此时root->left指向值为2的节点。
   • 再次检查根节点：
     • root->left->val（值为2）等于subRoot->val（值为2），进入isSameTree检查是否整棵树相同。
3. 调用isSameTree：
   • 调用isSameTree(root->left, subRoot)检查两棵树是否相同。
   • 首先检查根节点（值都为2），它们相同。
   • 递归检查左子树：
     • root->left->left->val（值为4）等于subRoot->left->val（值为4）。
     • 递归检查右子树：
       • root->left->right->val（值为5）等于subRoot->right->val（值为5）。
     • 由于左子树和右子树都相同，isSameTree返回true。
4. isSubtree函数继续执行：
   • 因为root->val == subRoot->val且isSameTree(root->left, subRoot)返回true，所以if (root->val == subRoot->val && isSameTree(root, subRoot))的条件成立，isSubtree返回true。
5. 注意：由于isSubtree函数在root->left就找到了匹配的子树，所以不会继续检查root->right。

最终，isSubtree函数返回true，因为subRoot是root的子树。

这个过程中，isSameTree函数被用来比较两棵树是否完全相同，而isSubtree函数则通过递归遍历root的所有子树，并调用isSameTree来检查是否存在与subRoot相同的子树。

二叉树遍历

 
 typedef struct BinTreeNode {
     int val;
      struct BinTreeNode *left;
     struct BinTreeNode *right;
 }BTNode;



BTNode* CreatTree(char*a,int* pi)
{
    if(a[*pi]=='#')
    {
        (*pi)++;
    return NULL;
    }
    BTNode* root=(BTNode*)malloc(sizeof(BTNode));//为新节点分配内存，并将其地址赋给 root 指针
    root->val=a[(*pi)++];
    root->left=CreatTree(a,pi);
    root->right=CreatTree(a,pi);
    return root;
}
int main()
{
    char a[100];
    scanf("%s",a);
    int i=0;
    BTNode*root=CreatTree(a,&i);
    return 0;
}

二叉树的最大深度 

104. 二叉树的最大深度 - 力扣（LeetCode）

int maxDepth(struct TreeNode *root) {
    if (root == NULL) return 0;
    return fmax(maxDepth(root->left), maxDepth(root->right)) + 1;
}

翻转二叉树 

226. 翻转二叉树 - 力扣（LeetCode）