手撕二叉搜索树

已于 2022-11-17 17:02:48 修改
阅读量1.1k 收藏 7
点赞数 12
分类专栏： 数据结构 文章标签： 算法 c++
于 2022-11-17 16:51:05 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/GG_Bruse/article/details/127816929
版权

目录

一、概念

二、常见操作

2.1 查找操作

2.2 插入操作

2.3 删除操作

三、模型应用

3.1 K模型

3.2 KV模型

3.3 代码完整实现

四、 性能分析

一、概念

二叉搜索树(BST,Binary Search Tree),也称二叉排序树或二叉查找树

它或者是一棵空树，或者是具有以下性质的二叉树:
1. 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
2. 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
3. 它的左右子树也分别为二叉搜索树
4. 不允许键值冗余

二、常见操作

2.1 查找操作

规则: a、从根开始比较，查找，比根大则往右边走查找，比根小则往左边走查找。
         b、最多查找高度次，若走到到空还没找到，则这个值不存在

非递归

bool find(const K& key) {
    BSTNode* cur = _root;
	while (cur != nullptr) {
    	if (cur->_key > key) {
        	cur = cur->_left;
	    }
	    else if (cur->_key < key) {
		    cur = cur->_right;
	    }
	    else {//cur->_key == key
		    return true;
	    }
    }
	return false;
}

递归

bool _find(BSTNode* root, const K& key) {
	if (root == nullptr) return false;

	else if (root->_key > key) return _find(root->_left, key);
	else if (root->_key < key) return _find(root->_right, key);
	else return true;//root->_key == key
}

bool find(const K& key) {
	return _find(_root, key);
}

2.2 插入操作

规则: a. 树为空，则直接新增节点，赋值给root指针
         b. 树不空，按二叉搜索树性质查找插入位置，插入新节点

非递归

bool insert(const K& key) {
    //树为空，则直接新增节点，赋值给root指针
	if (_root == nullptr) {
		_root = new BSTNode(key);
		return true;
	}

    //树不空，按二叉搜索树性质查找插入位置
	BSTNode* cur = _root, * parent = nullptr;
	while (cur != nullptr) {
		if (cur->_key > key) {
			parent = cur;
			cur = cur->_left;
		}
		else if (cur->_key < key) {
			parent = cur;
			cur = cur->_right;
		}
		else {//cur->_key == key
			return false;//不允许键值冗余，插入失败
		}
	}

    //插入新节点
	cur = new BSTNode(key);
	if (parent->_key > key) parent->_left = cur;
	else parent->_right = cur;

	return true;
}

递归

//root为上一层左指针(右指针)的别名，直接赋值即可
bool _insert(BSTNode*& root, const K& key) {
	if (root == nullptr) {
		root = new BSTNode(key);
		return true;
	}
	else if (root->_key > key) return _insert(root->_left, key);
	else if (root->_key < key) return _insert(root->_right, key);
	else return false;
}

bool insert(const K& key) {
	return _insert(_root, key);
}

2.3 删除操作

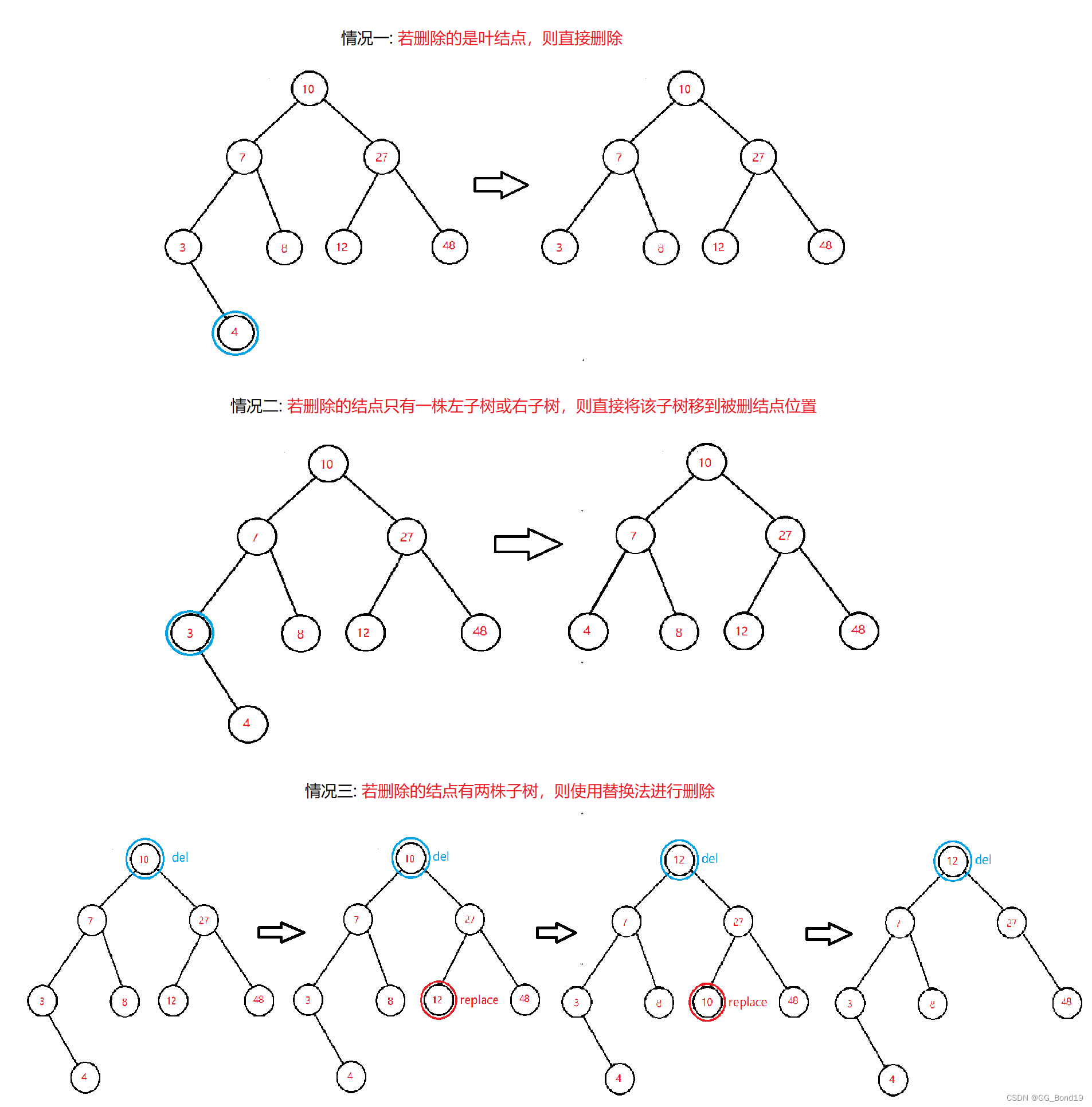
删除这个操作具有一定难度，为了使树在完成结点的删除后依然保持二叉树搜索树的性质，必须分情况进行处理。

(1)若删除的是叶结点，则直接删除

(2)若删除的结点只有一株左子树或右子树，则直接将该子树移到被删结点位置

(3)若删除的结点有两株子树，则使用替换法进行删除。在它的右子树中寻找中序下的第一个结点(关键码最小)，用它的值与待删除结点的值进行交换，再来处理该结点的删除问题

 非递归

bool erase(const K& key) {
	BSTNode* cur = _root, * parent = nullptr;
	while (cur != nullptr) {
		if (cur->_key > key) {
			parent = cur;
			cur = cur->_left;
		}
		else if (cur->_key < key) {
			parent = cur;
			cur = cur->_right;
		}
		else {//cur->_key == key,找到待删除结点，开始删除

            //待删除结点的左子树为空 或 待删除结点左右子树都为空
			if (cur->_left == nullptr) {
				if (cur == _root) {
					_root = cur->_right;
				}
				else {
					if (cur == parent->_left) {
						parent->_left = cur->_right;
					}
					if (cur == parent->_right) {
						parent->_right = cur->_right;
					}
				}
				delete cur;
				cur = nullptr;
			}
            
            //待删除结点的右子树为空
			else if (cur->_right == nullptr) {
				if (cur == _root) {
					_root = cur->_left;
				}
				else {
					if (cur == parent->_left) {
						parent->_left = cur->_left;
					}
					if (cur == parent->_right) {
						parent->_right = cur->_left;
					}
				}
				delete cur;
				cur = nullptr;
			}
            
            //左右都不为nullptr,使用替换法
			else {
                //找到待删除结点右子树的最小结点和其父结点
				BSTNode* replace = cur->_right, * min_parent = cur;
				while (replace->_left != nullptr) {
					min_parent = replace;
					replace = replace->_left;
				}
                //将最小结点的值与待删除结点的值进行交换
				swap(replace->_key, cur->_key);
                
                //最小结点不可能有左子树，接上右子树即可
				if (min_parent->_left == replace) {
					min_parent->_left = replace->_right;
				}
				else {
					min_parent->_right = replace->_right;
				}
				delete replace;
			}
			return true;
		}
	}
	return false;
}

递归

bool _erase(BSTNode*& root, const K& key) {
	if (root == nullptr) return false;

	else if (root->_key > key) return _erase(root->_left, key);
	else if (root->_key < key) return _erase(root->_right, key);

	else {//找到待删除结点
		BSTNode* del = root;

        //待删除结点的左子树为空或左右子树都为空
		if (root->_left == nullptr) {
			root = root->_right;
		}

        //待删除结点的右子树为空
		else if (root->_right == nullptr) {
			root = root->_left;
		}
        
        //左右都不为空
		else {
            //找到带删除结点右子树的最小结点
			BSTNode* replace = root->_right;
			while (replace->_left != nullptr) {
				replace = replace->_left;
			}
            //交换值
			swap(replace->_key, root->_key);

			return _erase(root->_right, key);
            //不可写成erase(key),因为重新查找不到
            //此时二叉搜索树的存储性质已被破坏，但待删除结点的右子树依然保持二叉搜索树的性质
		}
		delete del;
		return true;
	}	
}

bool erase(const K& key) {
	return _erase(_root, key);
}

三、模型应用

3.1 K模型

K模型即只有key作为关键码，结构中只需要存储Key即可，关键码即为需要搜索到的值
比如: 给一个单词word，判断该单词是否拼写正确，具体方式如下：以词库中所有单词集合中的每个单词作为key，构建一棵二叉搜索树在二叉搜索树中检索该单词是否存在，存在则拼写正确，不存在则拼写错误。

3.2 KV模型

每一个关键码key，都有与之对应的值value，即<Key, Value>的键值对
比如英汉词典就是英文与中文的对应关系，通过英文可以快速找到与其对应的中文，英文单词与其对应的中文<word, chinese>就构成一种键值对；
再比如统计单词次数，统计成功后，给定单词就可快速找到其出现的次数，单词与其出现次数就是<word, count>就构成一种键值对

3.3 代码完整实现

k模型

#define RECURSION
#include<iostream>
#include<algorithm>
using std::swap;
using std::cout;
using std::endl;
namespace KEY
{
	template<class K>
	struct BinarySearchTreeNode
	{
		BinarySearchTreeNode(const K& key = K()) : _left(nullptr), _right(nullptr), _key(key) {}
		BinarySearchTreeNode<K>* _left;
		BinarySearchTreeNode<K>* _right;
		K _key;
	};
	template<class K>
	class BinarySearchTree
	{
		typedef BinarySearchTreeNode<K> BSTNode;
	public:
		BinarySearchTree() = default;//C++11: 强制编译器生成默认构造
		BinarySearchTree(const BinarySearchTree<K>& obj) {
			_root = _copy(obj._root);
		}
		~BinarySearchTree() {
			_destory(_root);
		}
		BinarySearchTree<K>& operator=(BinarySearchTree<K> obj) {
			swap(_root, obj._root);
			return *this;
		}

		bool insert(const K& key) {
#ifdef RECURSION
			return _insert(_root, key);
#else
			if (_root == nullptr) {
				_root = new BSTNode(key);
				return true;
			}
			BSTNode* cur = _root, * parent = nullptr;
			while (cur != nullptr) {
				if (cur->_key > key) {
					parent = cur;
					cur = cur->_left;
				}
				else if (cur->_key < key) {
					parent = cur;
					cur = cur->_right;
				}
				else {//cur->_key == key
					return false;
				}
			}
			cur = new BSTNode(key);
			if (parent->_key > key) parent->_left = cur;
			else parent->_right = cur;
			return true;
#endif
		}

		bool erase(const K& key) {
#ifdef RECURSION
			return _erase(_root, key);
#else
			BSTNode* cur = _root, * parent = nullptr;
			while (cur != nullptr) {
				if (cur->_key > key) {
					parent = cur;
					cur = cur->_left;
				}
				else if (cur->_key < key) {
					parent = cur;
					cur = cur->_right;
				}
				else {//cur->_key == key
					if (cur->_left == nullptr) {
						if (cur == _root) {
							_root = cur->_right;
						}
						else {
							if (cur == parent->_left) {
								parent->_left = cur->_right;
							}
							if (cur == parent->_right) {
								parent->_right = cur->_right;
							}
						}
						delete cur;
						cur = nullptr;
					}
					else if (cur->_right == nullptr) {
						if (cur == _root) {
							_root = cur->_left;
						}
						else {
							if (cur == parent->_left) {
								parent->_left = cur->_left;
							}
							if (cur == parent->_right) {
								parent->_right = cur->_left;
							}
						}
						delete cur;
						cur = nullptr;
					}
					else {
						BSTNode* replace = cur->_right, * min_parent = cur;
						while (replace->_left != nullptr) {
							min_parent = replace;
							replace = replace->_left;
						}
						swap(replace->_key, cur->_key);
						if (min_parent->_left == replace) {
							min_parent->_left = replace->_right;
						}
						else {
							min_parent->_right = replace->_right;
						}
						delete replace;
					}
					return true;
				}
			}
			return false;
#endif 
		}

		bool find(const K& key) {
#ifdef RECURSION
			return _find(_root, key);
#else
			BSTNode* cur = _root;
			while (cur != nullptr) {
				if (cur->_key > key) {
					cur = cur->_left;
				}
				else if (cur->_key < key) {
					cur = cur->_right;
				}
				else {//cur->_key == key
					return true;
				}
			}
			return false;
#endif
		}

		void inorder() {
			_inorder(_root);
		}

	private:
		BSTNode* _copy(BSTNode* root) {
			if (root == nullptr) return nullptr;
			BSTNode* copy_root = new BSTNode(root->_key);
			copy_root->_left = _copy(root->_left);
			copy_root->_right = _copy(root->_right);
			return copy_root;
		}

		bool _insert(BSTNode*& root, const K& key) {//root为上一层左指针(右指针)的别名，直接赋值即可
			if (root == nullptr) {
				root = new BSTNode(key);
				return true;
			}
			else if (root->_key > key) return _insert(root->_left, key);
			else if (root->_key < key) return _insert(root->_right, key);
			else return false;
		}

		bool _erase(BSTNode*& root, const K& key) {
			if (root == nullptr) return false;
			else if (root->_key > key) return _erase(root->_left, key);
			else if (root->_key < key) return _erase(root->_right, key);
			else {
				BSTNode* del = root;
				if (root->_left == nullptr) {
					root = root->_right;
				}
				else if (root->_right == nullptr) {
					root = root->_left;
				}
				else {//左右都不为空
					BSTNode* replace = root->_right;
					while (replace->_left != nullptr) {
						replace = replace->_left;
					}
					swap(replace->_key, root->_key);
					return _erase(root->_right, key);
				}
				delete del;
				return true;
			}
		}

		bool _find(BSTNode* root, const K& key) {
			if (root == nullptr) return false;
			else if (root->_key > key) return _find(root->_left, key);
			else if (root->_key < key) return _find(root->_right, key);
			else return true;//root->_key == key
		}

		void _inorder(BSTNode* root) {
			if (root == nullptr) {
				return;
			}
			_inorder(root->_left);
			cout << root->_key << " ";
			_inorder(root->_right);
		}

		void _destory(BSTNode*& root) {
			if (root == nullptr) {
				return;
			}
			_destory(root->_left);
			_destory(root->_right);
			delete root;
			root = nullptr;
		}
	private:
		BSTNode* _root = nullptr;
	};
}

KV模型

namespace KEY_VALUE
{
	template<class K,class V>
	struct BinarySearchTreeNode
	{
		BinarySearchTreeNode(const K& key = K(), const V& value = V()) : _left(nullptr), _right(nullptr), _key(key), _value(value) {}
		BinarySearchTreeNode<K,V>* _left;
		BinarySearchTreeNode<K,V>* _right;
		K _key;
		V _value;
	};
	template<class K,class V>
	class BinarySearchTree
	{
		typedef BinarySearchTreeNode<K, V> BSTNode;
	public:
		bool insert(const K& key,const V& value) {
			if (_root == nullptr) {
				_root = new BSTNode(key,value);
				return true;
			}
			BSTNode* cur = _root, * parent = nullptr;
			while (cur != nullptr) {
				if (cur->_key > key) {
					parent = cur;
					cur = cur->_left;
				}
				else if (cur->_key < key) {
					parent = cur;
					cur = cur->_right;
				}
				else {//cur->_key == key
					return false;//不允许键值冗余，插入失败
				}
			}
			cur = new BSTNode(key,value);
			if (parent->_key > key) parent->_left = cur;
			else parent->_right = cur;
			return true;
		}

		BSTNode* find(const K& key) {
			BSTNode* cur = _root;
			while (cur != nullptr) {
				if (cur->_key > key) {
					cur = cur->_left;
				}
				else if (cur->_key < key) {
					cur = cur->_right;
				}
				else {//cur->_key == key
					return cur;
				}
			}
			return nullptr;
		}

		void inorder() {
			_inorder(_root);
		}
		private:
		void _inorder(BSTNode* root) {
			if (root == nullptr) {
				return;
			}
			_inorder(root->_left);
			cout << root->_key << ":" << root->_value << " ";
			_inorder(root->_right);
		}
	private:
		BSTNode* _root = nullptr;
	};
}

四、 性能分析

插入和删除操作都必须先查找，查找效率代表了二叉搜索树中各个操作的性能

对于同一个关键码集合，如果各关键码插入的次序不同，可能得到不同结构的二叉搜索树

最优情况下，二叉搜索树为完全二叉树(或者接近完全二叉树)，其平均比较次数为: log_2 N
最差情况下，二叉搜索树退化为单支树(或者类似单支)，若插入顺序有序即会出现单支的情况

问题:
若退化成单支树，二叉搜索树的性能就失去了。

那能否进行改进，不论按照什么次序插入关键码，二叉搜索树的性能都能达到最优？

使用AVL树和红黑树

评论 12
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

GG_Bond21

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值