求斐波那契数（递归和非递归）

斐波那契数的简介

斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家莱昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……

递归实现斐波那契数

#include<stdio.h>
int fib(int n)
{
    if(n<=2)
	{
	    return 1;
	}
	else
	{
	    return fib(n-1) + fib(n-2);
	}
}
int main()
{
	int n = 0;
	int ret = 0;
	scanf("%d",&n);
	ret = fib(n);
	printf("%d\n",ret);
	return 0;
}

在递归实现求斐波那契数中，存在着计算速度较慢的问题，原因出在大多数的数字重复运算，如下图:

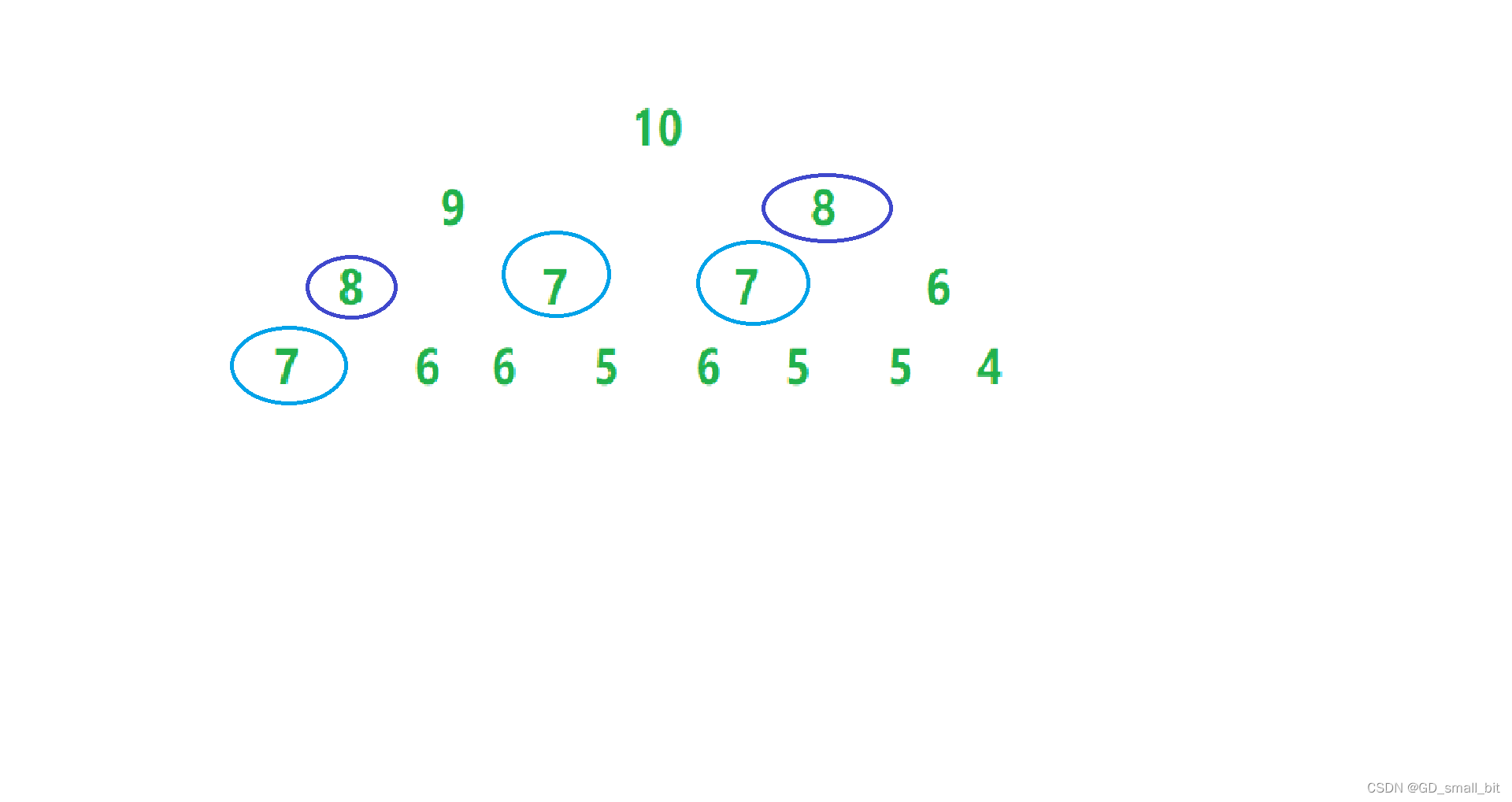
假设我们计算第十个斐波那契数，还没计算出结果，8就已经重复计算2次，7更是重复计算3次，由此可见，代码效率不高，所以我们采用非递归实现求斐波那契数。

非递归求斐波那契数

#include<stdio.h>
int fib(int n)
{
	int a = 1;
	int b = 1;
	int c = 1;
	while(n>2)
	{
	    c = a + b;
		a = b;
		b = c;
		n--;
	}
	return c;
}
int main()
{
	int n = 0;
	int ret = 0;
	scanf("%d",&n);
	ret = fib(n);
	printf("%d\n",ret);
	return 0;
}

今天的分享到这里，关注点一点，下期更精彩。