先行概念:
unitary matrix (酉矩阵)
two-level unitary matrix (two-level 的酉矩阵)
Gray code (格雷码)
circuit model
理论支持:
1.任意酉矩阵可以进行分解为two-level的酉矩阵,即对d维酉矩阵有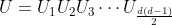
2.任意two-level的酉矩阵可以用单量子门与two-level的酉矩阵构建
构建步骤:
1.将运算的酉矩阵进行分解,分解的步骤如下:
- 将矩阵的第一列除第一行外的每一行利用two-level的酉矩阵全部变零,以上面的U矩阵为例,则
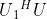 的结果应该是使得U的二行一列为零。若U为
的结果应该是使得U的二行一列为零。若U为
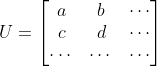
则
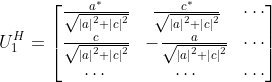
其余对角线均为1。然后对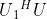 矩阵的第一行第三列进行操作得到
矩阵的第一行第三列进行操作得到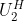 ,重复这一步骤得到第一列除第一行外全为零的矩阵
,重复这一步骤得到第一列除第一行外全为零的矩阵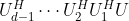
- 对一步得到的矩阵,对以第二行第二列开始的矩阵重复操作使得第二行除第二列不为零其余全为零。重复这一步骤得到除右下角2*2的矩阵外其余矩阵中只有对角线上非零的矩阵








 本文介绍了如何通过分解酉矩阵为two-level单元,并结合单量子门与受控非门来构建任意酉矩阵的量子运算门。首先,详细解释了酉矩阵的分解步骤,然后阐述了two-level矩阵的构建方法,利用格雷码和受控非门进行状态转换。通过MATLAB代码辅助理解,展示了具体的量子门构造过程。
本文介绍了如何通过分解酉矩阵为two-level单元,并结合单量子门与受控非门来构建任意酉矩阵的量子运算门。首先,详细解释了酉矩阵的分解步骤,然后阐述了two-level矩阵的构建方法,利用格雷码和受控非门进行状态转换。通过MATLAB代码辅助理解,展示了具体的量子门构造过程。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1562
1562

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








