2019年 7月29日--8月4日 周报

最新推荐文章于 2022-12-02 08:00:31 发布
原创 最新推荐文章于 2022-12-02 08:00:31 发布 · 669 阅读 · 4 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#EEGLAB #频谱分析 #串口通信 #fadtool #MATLAB

本文介绍了使用MATLAB处理脑电数据的技巧，包括数据截取、带通滤波器设计、归一化频谱分析，以及Python上位机串口通信的常见问题。通过实际案例展示了静息态和癫痫态小鼠脑电数据的处理过程。

2019年 7月29日--8月4日 课题组周汇报_目录

8月4日 周报

(一)本周进展及下周计划

本周进展：
1.学习直接用MATALB对原始脑电数据进行处理，而不依赖于EEGLAB工具箱；
2.学习python及串口通信，想办法解决python上位机存在的bug.

存在的问题：
1.超声课题组的各位都放假回家了，实验进度停滞，日报无材料可写；
2.python上位机的bug找到了，正在想办法解决.

下周计划：
1.把python上位机的问题解决掉；
2.开始抽时间去推进PLADRC论文的工作。

(二)具体进展情况

1. 从脑电数据中截取某一段的方法

环境需求：画图用MATLAB R2018a，查看eeg用MATALB R2013b中的EEGLAB，EEGLAB版本为v13.0.1
方法：在EEGLAB中遍历脑电数据，找到自己感兴趣的eeg片段，记下它的时间节点，然后在MATLAB R2018a中画图

(1) 在EEGLAB中遍历脑电数据，找到自己感兴趣的某一段
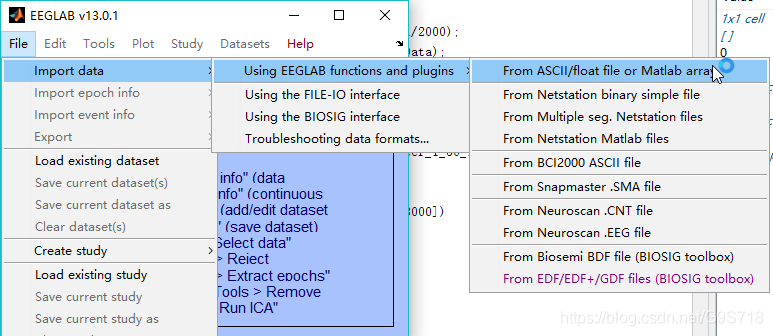
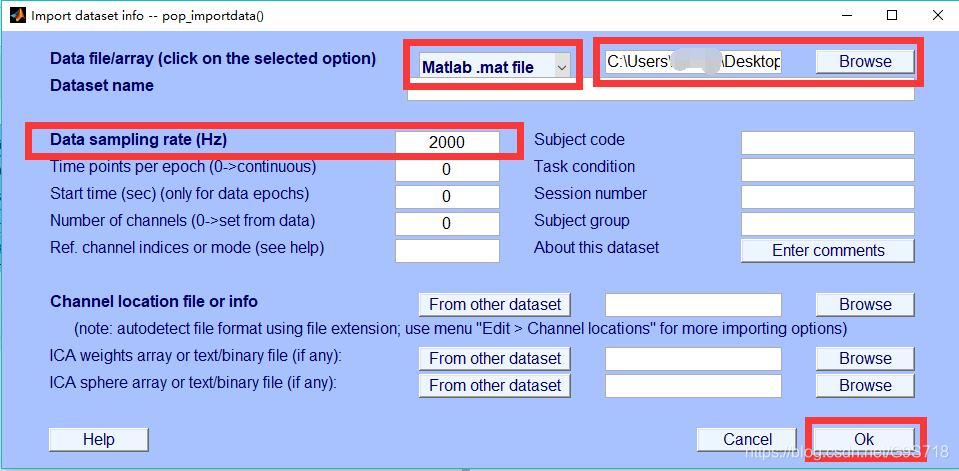
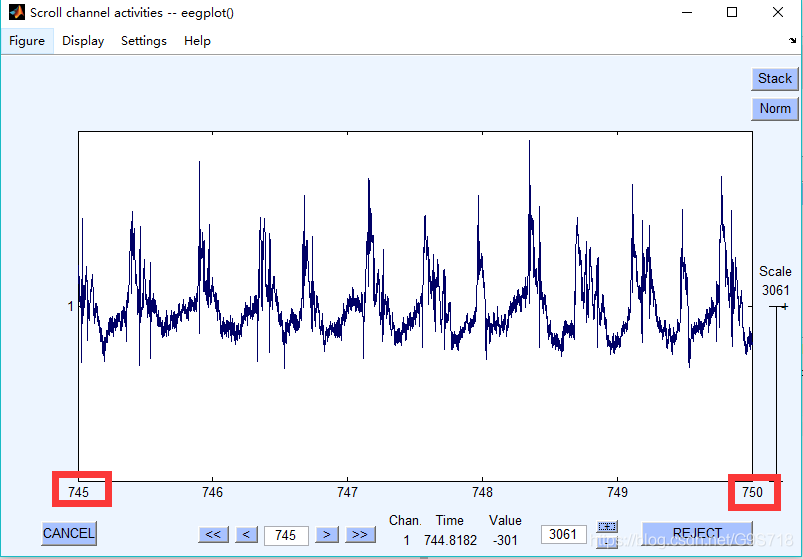
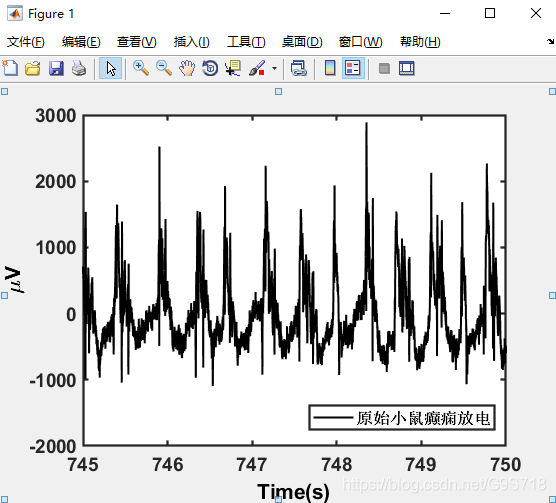
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
745~750s出现癫痫放电，我们对这段eeg很感兴趣，接下来要在MATLAB R2018a中将它画出来，并且分析它.

(2)在MATLAB R2018a中将745~750s的脑电数据画出来（无刺激时的癫痫状放电，文件夹1-1的数据）

clc;
clear;
close all;

openNSx('read');
t=745:(1/2000):750;
eega=double(NS3.Data);
eegn=eega(745*2000:750*2000);

figure(1)
plot(t,eegn,'k','linewidth',1.5);

l1=legend('原始小鼠癫痫放电');
set(l1,'linewidth',1.6,'fontsize',12,'fontweight','bold');
xlabel('Time(s)','fontsize',16,'fontweight','bold');
ylabel('\muV','fontsize',16,'fontweight','bold');
set(gca, 'linewidth',1.6,'fontsize',14,'fontweight','bold')
axis([745 750 -2000 3000]);

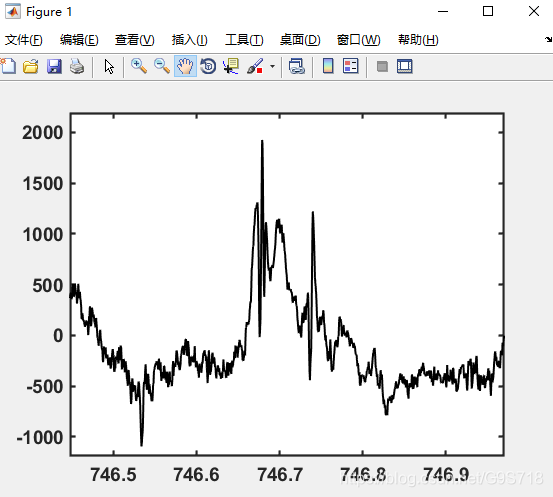
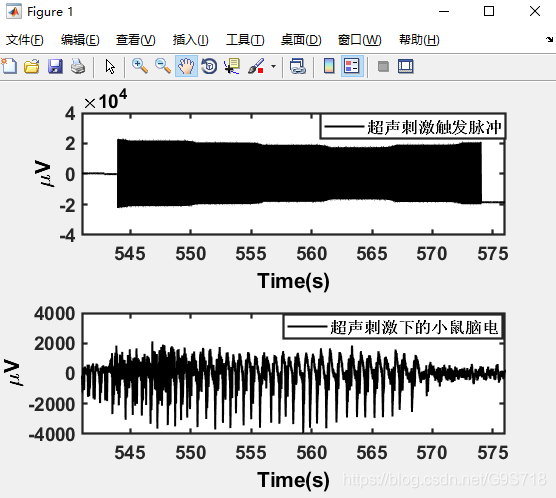
在这里插入图片描述在这里插入图片描述
(3) 同理，现在画有刺激时的癫痫状放电及其刺激信号（文件夹2-2的数据）
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
注：这里打开的显然是降频滞后的刺激信号，原数据是30000Hz的方波，现在在EEGLAB中将其以采样率2000Hz打开，所以才变成了类似三角波的信号.

clc;
clear;
close all;

warning('选择脑电数据的ns5数据,文件夹2-2');
openNSx('read');
warning('选择脑电数据的ns3数据，文件夹2-2');
openNSx('read');

t=541:(1/2000):576;

eega=double(NS3.Data);
eegn=eega(541*2000:576*2000);

tusa=double(NS5.Data);
tusp=resample(tusa,2000,30000);
tusn=tusp(541*2000:576*2000);

figure(1)
subplot(2,1,1)
plot(t,tusn,'k','linewidth',1.5);
l1=legend('超声刺激触发脉冲');
set(l1,'linewidth',1.6,'fontsize',12,'fontweight','bold');
xlabel('Time(s)','fontsize',16,'fontweight','bold');
ylabel('\muV','fontsize',16,'fontweight','bold');
set(gca, 'linewidth',1.6,'fontsize',14,'fontweight','bold');
axis([541 576 -4e4 4e4]);

subplot(2,1,2)
plot(t,eegn,'k','linewidth',1.5);
l2=legend('超声刺激下的小鼠脑电');
set(l2,'linewidth',1.6,'fontsize',12,'fontweight','bold');
xlabel('Time(s)','fontsize',16,'fontweight','bold');
ylabel('\muV','fontsize',16,'fontweight','bold');
set(gca, 'linewidth',1.6,'fontsize',14,'fontweight','bold')
axis([541 576 -4000 4000]);

在这里插入图片描述
(4)没有经过resample(tusp,2000,30000)改变采样率时的超声刺激信号(文件2-2)
在这里插入图片描述
arun_waveform 源码：

clear all
close all
clc%是否以超声开始点作为0时刻点，false为超声结束点
%一般以超声开始点为0时刻点，但画图的时候记得标注超声结束点
is_use_start=true;

%运行的时候会要求依次打开数据
warning('选择脑电数据的ns3数据');
openNSx('read');
warning('选择超声数据的ns5数据');
openNSx('read');
%%%%%%%%%%%画波形图

eega=double(NS3.Data);
eeg_srate=NS3.MetaTags.SamplingFreq;
clear NS3;

tusa=double(NS5.Data);
tus_srate=NS5.MetaTags.SamplingFreq;
clear NS5;
sample_rate_1=2000;
sample_rate_2=30000;
tus=resample(tusa,sample_rate_1,sample_rate_2);

eegn=eega(1:end);
tus_p=tus(1:end);

figure;
subplot(2,1,1)
plot(eegn);
subplot(2,1,2)
plot(tus_p);

从源码中可以开出tusa是未经改变采样率之前的超声刺激触发信号，从MATLAB的workplace中将其另存为出来，然后导入EEGLAB 中查看.
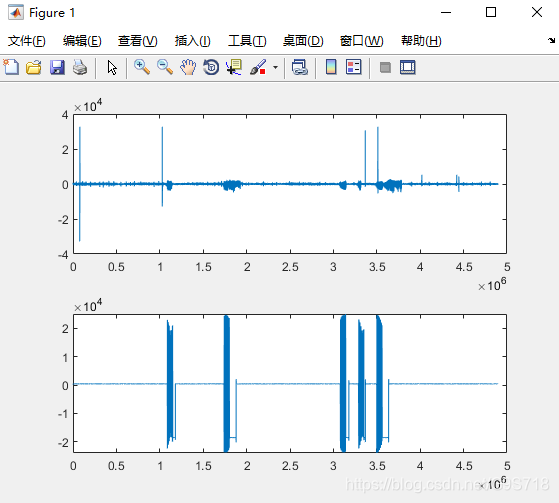
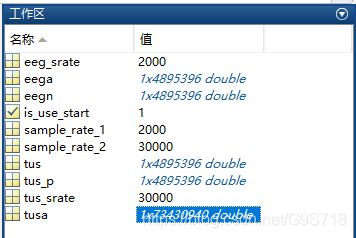
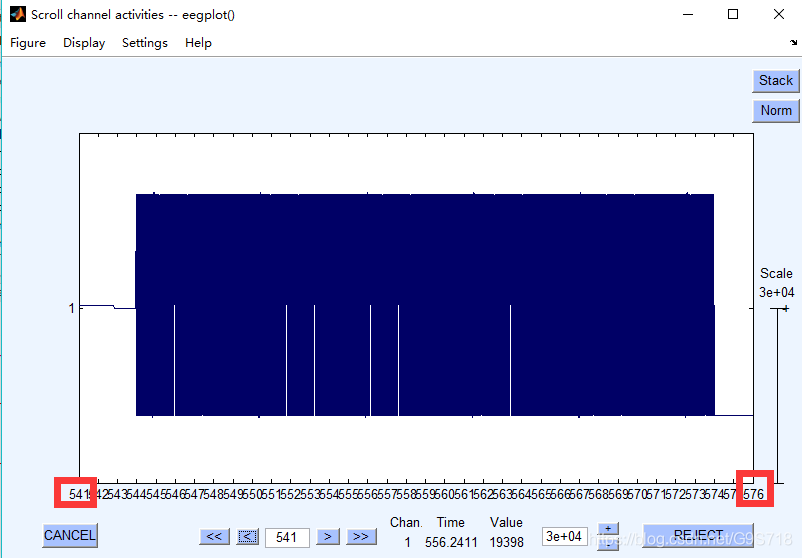
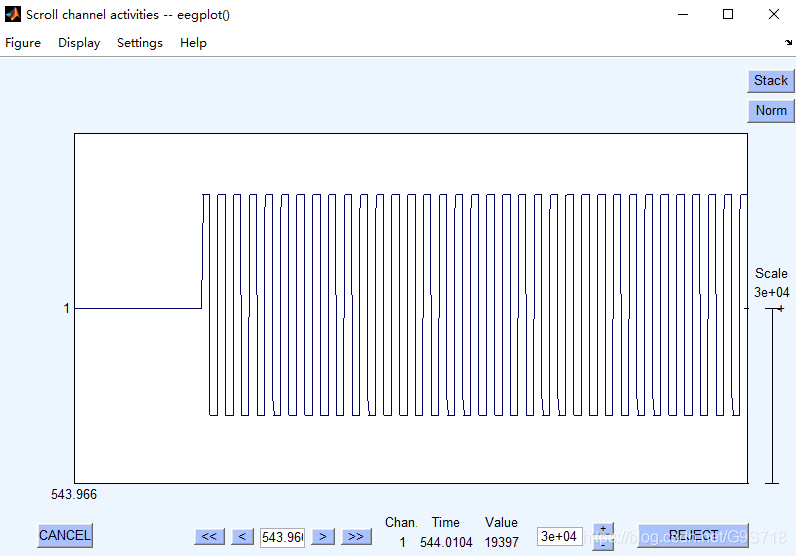
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
所以说之前我们采集到的根本不是什么超声刺激信号，只是触发信号而已.

2. (1~50Hz)带通滤波器的设计

设计环境：MATLAB R2018a—fdatool

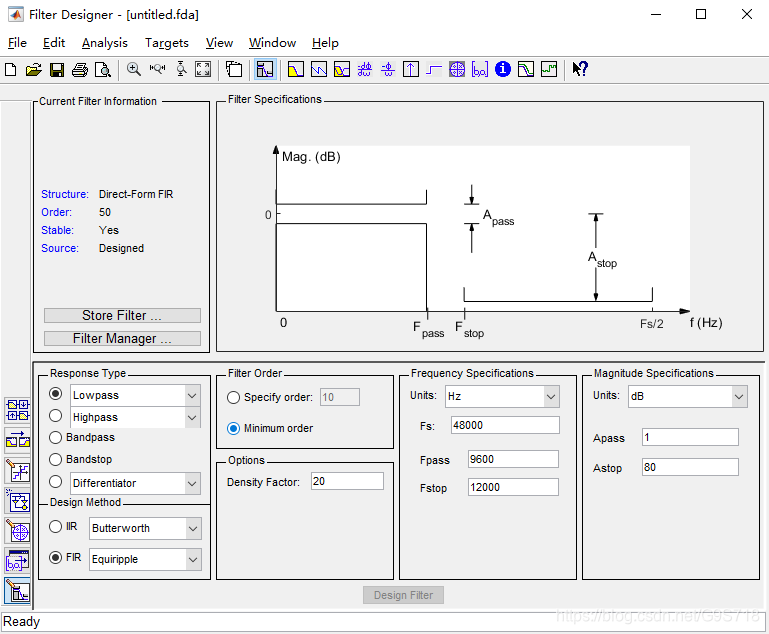
在这里插入图片描述
EEGLAB中1~50Hz的FIR滤波器
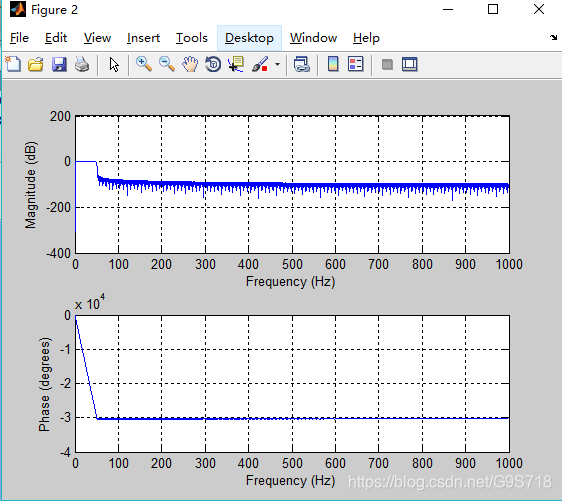
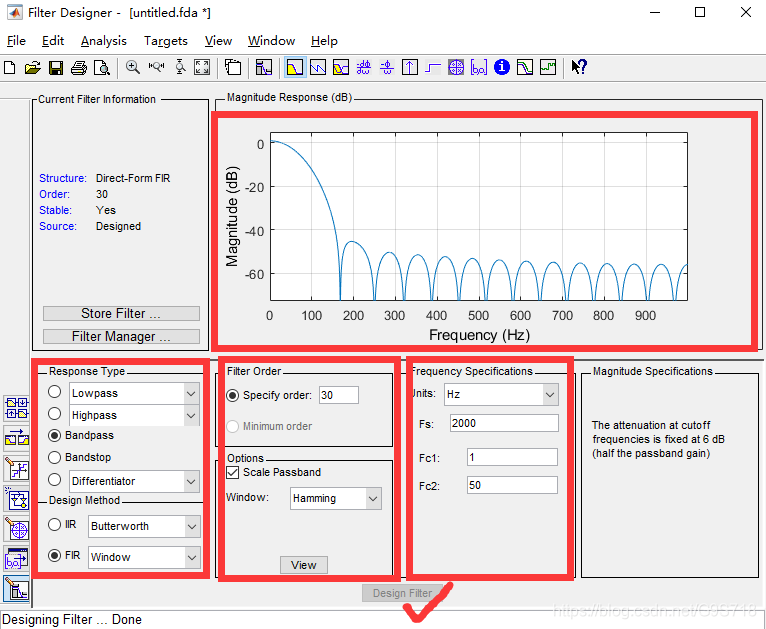
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
fdatool生成的滤波器函数：

function Hd = filter1_50
%FILTER_1-50 Returns a discrete-time filter object.

% MATLAB Code
% Generated by MATLAB(R) 9.4 and Signal Processing Toolbox 8.0.
% Generated on: 04-Aug-2019 20:18:11

% FIR Window Bandpass filter designed using the FIR1 function.

% All frequency values are in Hz.
Fs = 2000;  % Sampling Frequency

N    = 30;       % Order
Fc1  = 1;        % First Cutoff Frequency
Fc2  = 50;       % Second Cutoff Frequency
flag = 'scale';  % Sampling Flag
% Create the window vector for the design algorithm.
win = hamming(N+1);

% Calculate the coefficients using the FIR1 function.
b  = fir1(N, [Fc1 Fc2]/(Fs/2), 'bandpass', win, flag);
Hd = dfilt.dffir(b);

% [EOF]

然后只要在MATALB中直接调用这个函数就可以实现滤波了

eegn_filter=filter(filter1_50,eegn);

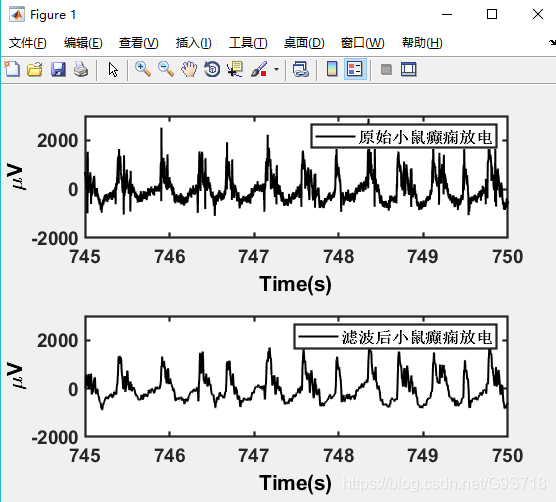
接下来我们来试试看效果如何.

clc;
clear;
close all;

warning('文件夹1-1的eeg');
openNSx('read');
t=745:(1/2000):750;
eega=double(NS3.Data);
eegn=eega(745*2000:750*2000);

% 1-50Hz带通滤波
eegn_filter=filter(filter1_50,eegn);

% 绘图
figure(1)

subplot(2,1,1)
plot(t,eegn,'k','linewidth',1.5);

l1=legend('原始小鼠癫痫放电');
set(l1,'linewidth',1.6,'fontsize',12,'fontweight','bold');
xlabel('Time(s)','fontsize',16,'fontweight','bold');
ylabel('\muV','fontsize',16,'fontweight','bold');
set(gca, 'linewidth',1.6,'fontsize',14,'fontweight','bold')
axis([745 750 -2000 3000]);

subplot(2,1,2)
plot(t,eegn_filter,'k','linewidth',1.5);

l2=legend('滤波后小鼠癫痫放电');
set(l2,'linewidth',1.6,'fontsize',12,'fontweight','bold');
xlabel('Time(s)','fontsize',16,'fontweight','bold');
ylabel('\muV','fontsize',16,'fontweight','bold');
set(gca, 'linewidth',1.6,'fontsize',14,'fontweight','bold')
axis([745 750 -2000 3000]);

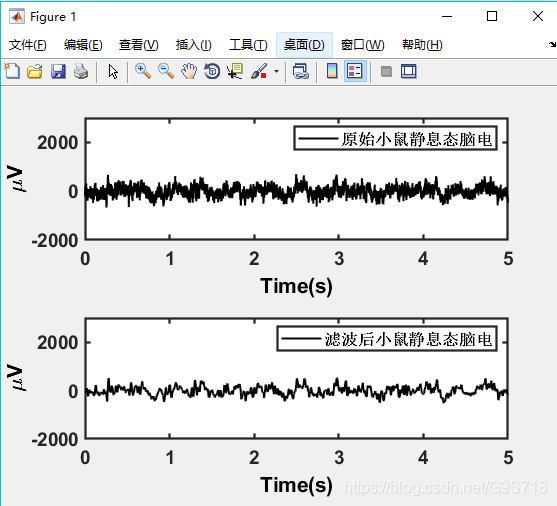
在这里插入图片描述
就按照这种方式，我们试着画出静息态的eeg并且滤波

clc;
clear;
close all;

warning('文件夹1-2的eeg');
openNSx('read');
t=0:(1/2000):5-1/2000;
eega=double(NS3.Data);
eegn=eega(1:5*2000);

% 1-50Hz带通滤波
eegn_filter=filter(filter1_50,eegn);

% 绘图
figure(1)

subplot(2,1,1)
plot(t,eegn,'k','linewidth',1.5);

l1=legend('原始小鼠静息态脑电');
set(l1,'linewidth',1.6,'fontsize',12,'fontweight','bold');
xlabel('Time(s)','fontsize',16,'fontweight','bold');
ylabel('\muV','fontsize',16,'fontweight','bold');
set(gca, 'linewidth',1.6,'fontsize',14,'fontweight','bold')
axis([0 5 -2000 3000]);

subplot(2,1,2)
plot(t,eegn_filter,'k','linewidth',1.5);

l2=legend('滤波后小鼠静息态脑电');
set(l2,'linewidth',1.6,'fontsize',12,'fontweight','bold');
xlabel('Time(s)','fontsize',16,'fontweight','bold');
ylabel('\muV','fontsize',16,'fontweight','bold');
set(gca, 'linewidth',1.6,'fontsize',14,'fontweight','bold')
axis([0 5 -2000 3000]);

在这里插入图片描述

3. 归一化频谱分析方法

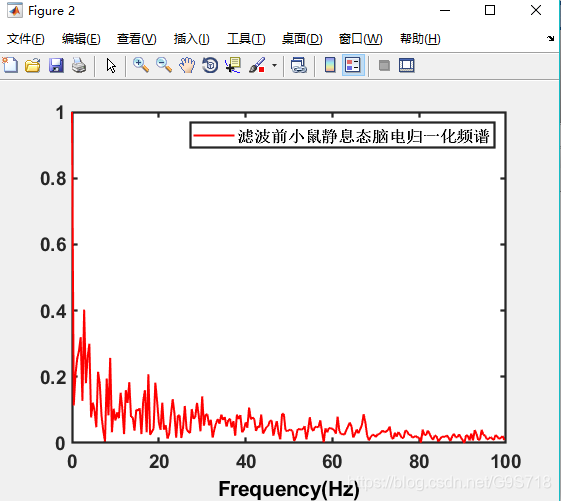
李小俚老师文章中的归一化频谱分析实例在这里插入图片描述在这里插入图片描述

（1）静息态小鼠脑电滤波前后的归一化频谱分析

滤波前 的小鼠 静息态 脑电归一化频谱：

clc;
clear;
close all;

warning('文件夹1-2的eeg');
openNSx('read');
t=0:(1/2000):5-1/2000;
eega=double(NS3.Data);
eegn=eega(1:5*2000);

% 1-50Hz带通滤波
eegn_filter=filter(filter1_50,eegn);

% 归一化频谱分析
t1=0:1/500:1;%采样步长
y= eegn;
N=length(t1); %样点个数
fs=200;%采样频率
df=fs/(N-1);%分辨率
f=(0:N-1)*df;%其中每点的频率
Y=fft(y(1:N))/N*2;%真实的幅值
Y_gui1=mapminmax(Y,0,1); %幅值归一化
%Y=fftshift(Y);

% 绘图1(滤波前后的脑电)
figure(1)

subplot(2,1,1)
plot(t,eegn,'k','linewidth',1.5);

l1=legend('原始小鼠静息态脑电');
set(l1,'linewidth',1.6,'fontsize',12,'fontweight','bold');
xlabel('Time(s)','fontsize',16,'fontweight','bold');
ylabel('\muV','fontsize',16,'fontweight','bold');
set(gca, 'linewidth',1.6,'fontsize',14,'fontweight','bold')
axis([0 5 -2000 3000]);

subplot(2,1,2)
plot(t,eegn_filter,'k','linewidth',1.5);

l2=legend('滤波后小鼠静息态脑电');
set(l2,'linewidth',1.6,'fontsize',12,'fontweight','bold');
xlabel('Time(s)','fontsize',16,'fontweight','bold');
ylabel('\muV','fontsize',16,'fontweight','bold');
set(gca, 'linewidth',1.6,'fontsize',14,'fontweight','bold')
axis([0 5 -2000 3000]);

% 绘图2(归一化频谱)
figure(2)
plot(f(1:N/2),abs(Y_gui1(1:N/2)),'r','linewidth',1.5);

l3=legend('滤波前小鼠静息态脑电归一化频谱');
set(l3,'linewidth',1.6,'fontsize',12,'fontweight','bold');
xlabel('Frequency(Hz)','fontsize',16,'fontweight','bold');
set(gca, 'linewidth',1.6,'fontsize',14,'fontweight','bold')

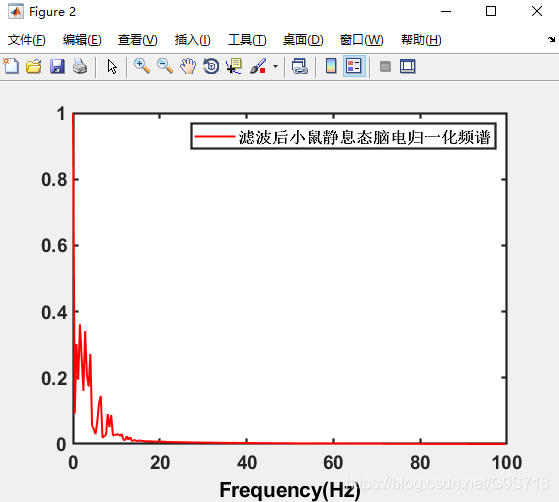
在这里插入图片描述
滤波后的归一化频谱只需将

y=eegn;

l3=legend('滤波前小鼠静息态脑电归一化频谱');

改为

y=eegn_filter

l3=legend('滤波后小鼠静息态脑电归一化频谱');

就可以了
在这里插入图片描述

（2）癫痫态小鼠脑电滤波前后的归一化频谱分析

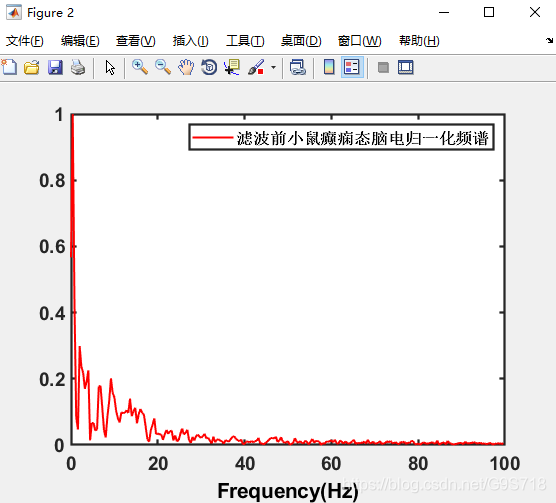
滤波前 的小鼠 癫痫态 脑电归一化频谱：

clc;
clear;
close all;

warning('文件夹1-1的eeg');
openNSx('read');
t=745:(1/2000):750;
eega=double(NS3.Data);
eegn=eega(745*2000:750*2000);

% 1-50Hz带通滤波
eegn_filter=filter(filter1_50,eegn);

% 归一化频谱分析
t1=0:1/500:1;%采样步长
y= eegn;
N=length(t1); %样点个数
fs=200;%采样频率
df=fs/(N-1);%分辨率
f=(0:N-1)*df;%其中每点的频率
Y=fft(y(1:N))/N*2;%真实的幅值
Y_gui1=mapminmax(Y,0,1); %幅值归一化
%Y=fftshift(Y);

% 绘图1(滤波前后的脑电)
figure(1)

subplot(2,1,1)
plot(t,eegn,'k','linewidth',1.5);

l1=legend('原始小鼠癫痫态脑电');
set(l1,'linewidth',1.6,'fontsize',12,'fontweight','bold');
xlabel('Time(s)','fontsize',16,'fontweight','bold');
ylabel('\muV','fontsize',16,'fontweight','bold');
set(gca, 'linewidth',1.6,'fontsize',14,'fontweight','bold')
axis([745 750 -2000 3000]);

subplot(2,1,2)
plot(t,eegn_filter,'k','linewidth',1.5);

l2=legend('滤波后小鼠癫痫态脑电');
set(l2,'linewidth',1.6,'fontsize',12,'fontweight','bold');
xlabel('Time(s)','fontsize',16,'fontweight','bold');
ylabel('\muV','fontsize',16,'fontweight','bold');
set(gca, 'linewidth',1.6,'fontsize',14,'fontweight','bold')
axis([745 750 -2000 3000]);

% 绘图2(归一化频谱)
figure(2)
plot(f(1:N/2),abs(Y_gui1(1:N/2)),'r','linewidth',1.5);

l3=legend('滤波前小鼠癫痫态脑电归一化频谱');
set(l3,'linewidth',1.6,'fontsize',12,'fontweight','bold');
xlabel('Frequency(Hz)','fontsize',16,'fontweight','bold');
set(gca, 'linewidth',1.6,'fontsize',14,'fontweight','bold')

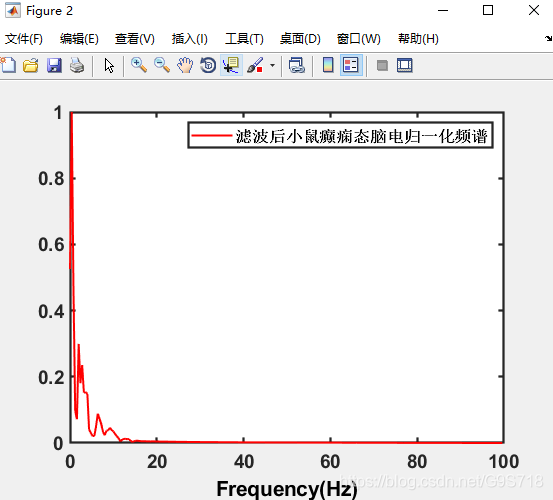
在这里插入图片描述
滤波后的归一化频谱只需将

y=eegn;

l3=legend('滤波前小鼠静息态脑电归一化频谱');

改为

y=eegn_filter

l3=legend('滤波后小鼠静息态脑电归一化频谱');

就可以了
在这里插入图片描述

4. 关于python上位机串口通信的若干问题

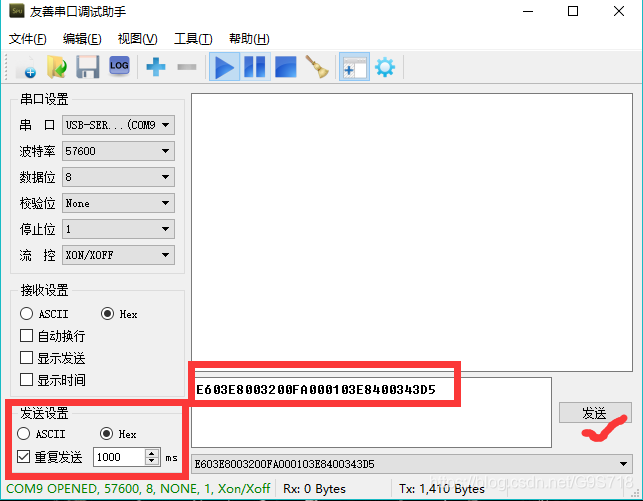
在这里插入图片描述
我试了试，把03E8、0032等中的0去掉也是无法成功通信的，不过加空格是可以的,如：
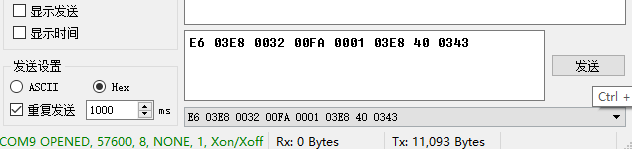
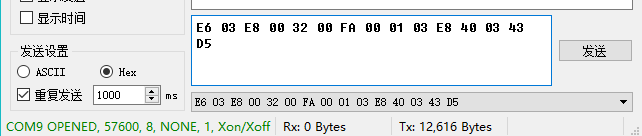
在这里插入图片描述
在这里插入图片描述
连这样也是可以的：
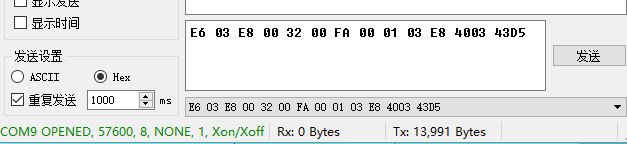
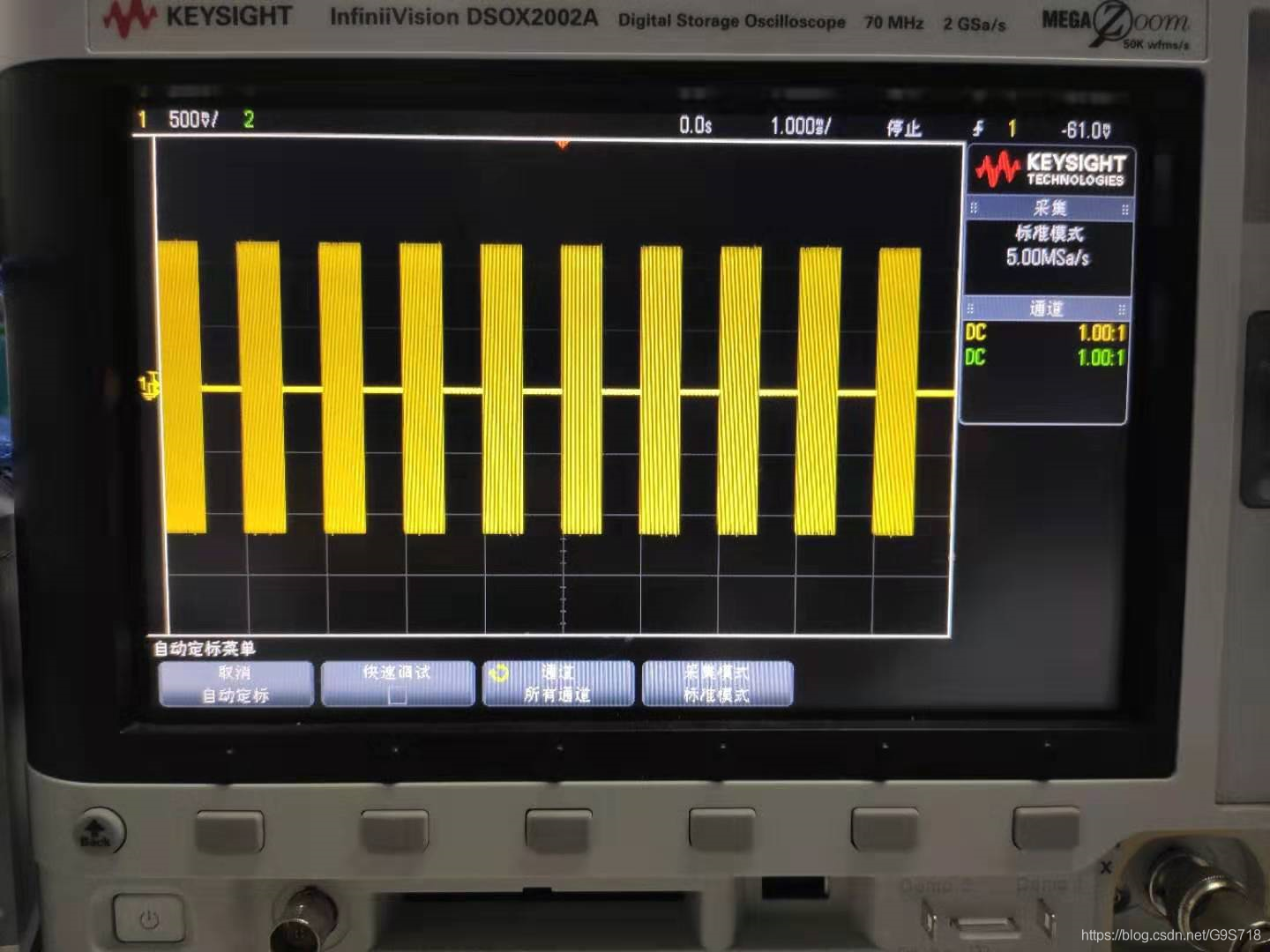
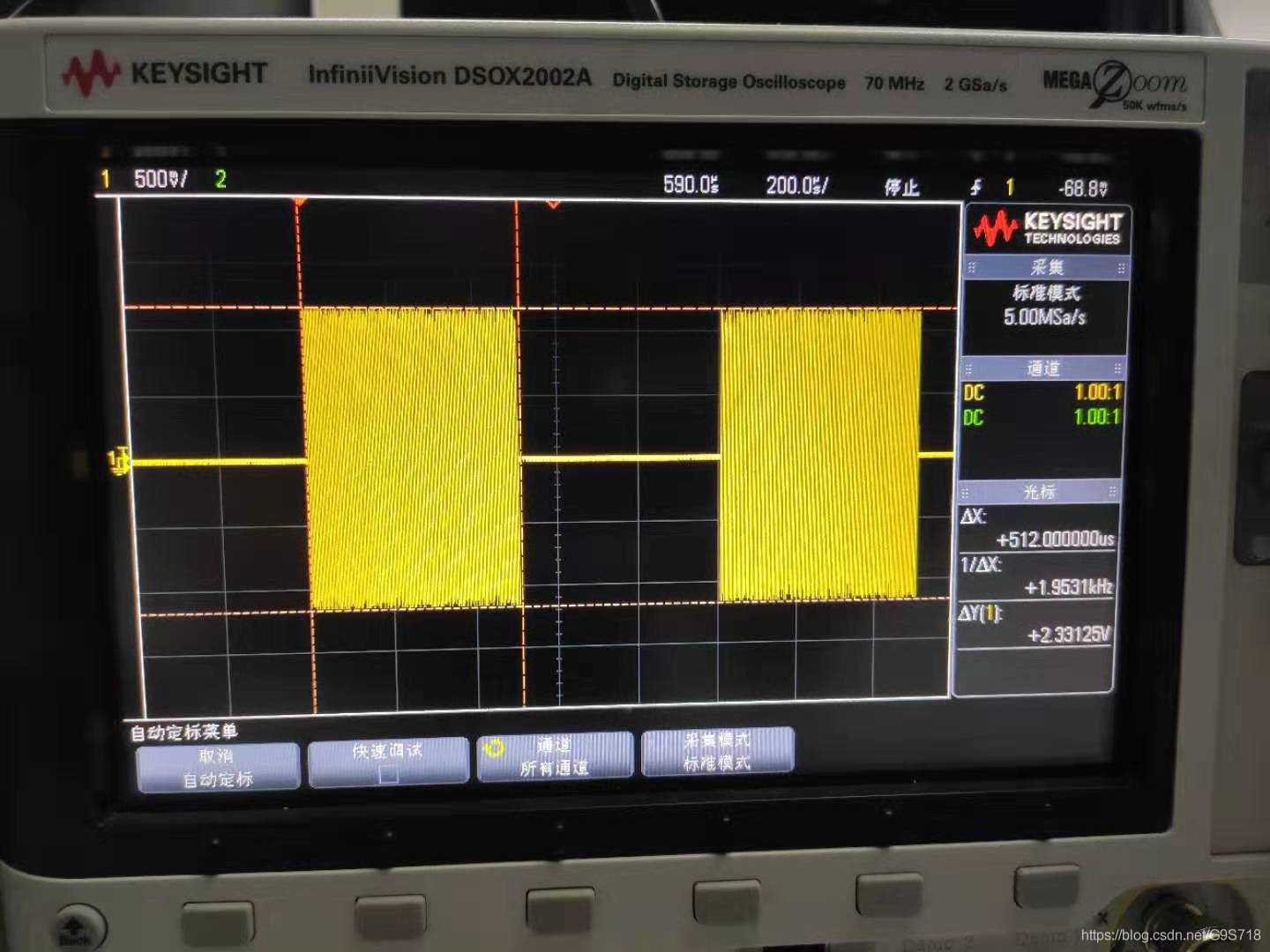
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
python上位机之所以发送无效可能是因为它发送的只是字符串而非hex发送.

附录

常用希腊字母英文

在这里插入图片描述

#Matlab# 调用 eeglab 包实现 批量 绘制 脑电 拓扑图
lch551218的博客
01-02 1万+
使用topoplot函数可以轻松实现在matlab的fgure中绘制脑电拓扑图，但对于大量数据，如果每次都手动调用topoplot绘制单张拓扑图片，将会消耗大量时间和经历，这里手写了一个matlab脚本读取存放在excel文件中的批量数据并实现批量绘图。 1.数据源的存储结构 数据源为excel文件，excel文件内的数据截图如下： 数据基本分为三个部分：特征列，数据列和电极点列，其中： 特征...
TOP Network项目双周报：2019年11月4日 - 11月17日
TOP_Network的博客
11-20 668
TOP主网上线后，我们的周报将改回为双周报，在隔周的每周二为您整理发布项目最新进展。感谢各位社区成员的支持和信任，TOP一路有你们，将继续再创新高！ 重磅消息 11月8日，TOP Network 主网上线发布会在浙江乌镇 “第二届世界区块链大会” 圆满结束。本次发布会以 “创新 · 落地 · 破局” 为主题，现场上百名区块链行业领袖、媒体、开发者等共同见证TOP重要技术进展的突破。TOP创始团队...
Qtum量子链周报（7月29日-8月4日）
weixin_42667079的博客
08-06 293
Qtum 量子链 7月29日-8月4日 新闻动态回顾 本篇文章会详细回顾 Qtum 量子链在过去的一周（7月29日- 8月4日）项目动态，新闻回顾后还包含 Qtum 所有目前技术开发进展，欢迎随时查阅。 Qtum量子链全节点激励计划第三期火热进行中！ 活动时间：7月15日-10月23日（东八区） 每2小时开奖一次，24小时滚动抽奖 剩余名额：942 如...
Qtum量子链周报（4月29日-5月5日）
weixin_42667079的博客
05-07 128
Qtum 量子链4月29日-5月5日 新闻动态回顾 本篇文章会详细回顾 Qtum 量子链在过去的一周（4月29日- 5月5日）项目动态，新闻回顾后还包含 Qtum 所有目前技术开发进展，欢迎随时查阅。 谷歌云推出Qtum量子链开发工具 开启智能云计算新时代 2019年5月2日，谷歌云正式推出了Qtum量子链开发工具包，遍布全球的谷歌云端服务器资源和快速安全的Qtum开...
.NET周报【11月第4期 2022-11-30】
dotNET跨平台
12-02 1448
国内文章.NET 7 的 AOT 到底能不能扛反编译？https://www.cnblogs.com/huangxincheng/p/16917197.html在 B 站，公众号上发了一篇 AOT 的文章后，没想到反响还是挺大的，都称赞这个东西能抗反编译，可以让破解难度极大提高，可能有很多朋友对逆向不了解，以为用 ILSpy,Reflector,DnSpy 这些工具打不开就觉得很安全，其实不然，在...
InterValue项目周报：20190826-20190901
Intervalue的博客
09-04 209
一、InterValue开发进度 1、INVE主网：继续进行两个节点同步数据保存功能与对方数据分布功能的开发；继续进行服务器端数据（产生HashRoot和可验证的Event）提供功能的开发；进行节点数据同步全新节点——检测最新的First Seqs编码；进行节点数据同步全新节点——数据来源端的全部代码调试；修改Local full node v2初始化流程；编写Zabbix监控脚本；进行主网运行...
InterValue项目周报：20190513-20190519
Intervalue的博客
05-22 300
一、InterValue开发进度 1、INVE主网：对快照剥离代码进行review，对快照功能模块进行测试网联调，详细记录并解决发现的问题。对程序原始多线程进行单线程化。对每日交易数据进行同步存储本地2次，并进行数据完整性验证。对rocksDB结构设计进行回归分析。查询世界状态，确保世界状态一致性。编写跟踪器程序应用跟踪HashNet Core测试与ICE网络测试情况。撰写跟踪程序应用说明，并完...
根据指定时间获取时间（日，周，月，季度，年）
weixin_55713874的博客
09-15 472
java获取时间
InterValue项目周报：20190318-20190324
Intervalue的博客
03-26 352
一、InterValue开发进度 1、项目进度 (1) INVE主网：升级并维护主网共识算法，进一步提升网络稳定性。 (2) 中继节点：升级并维护中继节点代码。 (3) inWallet：完成网页版钱包产品原型设计及评审。 (4) 主网映射：优化映射页面用户体验，增加取消关闭弹窗提示。 2、白皮书 (1) 一些常规性的细节修改。 二、战略合作 1、与FCoin对接主网映射事宜。 三、社群公告 1...
申万宏源2019年4月29日造纸轻工行业分析报告
8. 报告发布日期：2019年4月29日，这个日期对于投资者来说很重要，因为报告反映的是那个时间点的行业状况和公司业绩。随着时间的推移，相关数据和市场环境可能会发生变化，因此报告的时效性也是投资者需要考虑的因素...
基础化工行业2019年7月份第4期周报：河南义马爆炸引醋酸价格暴涨，聚酯工厂减产PTA宽幅下跌.pdf
08-21
【基础化工行业2019年7月份第4期周报】主要反映了中国化工市场在2019年7月29日时的情况，特别是醋酸和PTA的价格变动。报告指出，河南义马的爆炸事件对醋酸市场产生了重大影响，导致其价格暴涨。事故发生后，全国醋酸...
汽车行业周报：3月前四周乘用车市场零售同比2019年下降5%.pdf
07-02
例如，文档中提到汽车行业在2021年3月29日至4月4日这一周的市场表现，以及沪深300、创业板的涨跌情况，这可以帮助投资者对整个行业和股市的走向有一个大致的了解。 2. 细分行业表现：对汽车行业进行细分，可以发现...
计算机行业周报：计算机行业2019年中报总体符合预期，部分公司表现突出.pdf
07-07
4. 市场走势和投资策略：在2019年7月8日至7月12日的一周中，沪深300指数下跌2.17%，而计算机行业下跌5.16%，显示出行业在此期间的表现并未优于大盘。在这样的背景下，周报提出了一些投资策略建议，并对云计算、人工...
房地产2019年第27周地产周报：销售显现压力，土地市场略有回落.pdf
07-09
房地产行业在2019年第27周（2019年6月29日至7月5日）显示出了一定的压力和调整迹象，主要体现在以下几个方面： 1. 市场整体表现：在这一周，房地产板块指数表现强于创业板指和沪深300指数，整体表现相对较好，显示...
elasticsearch-7.17.22-linux-x86-64.tar.gz分享给需要的同学
12-08
elasticsearch-7.17.22-linux-x86_64.tar.gz分享给需要的同学
rocketmq-dashboard 1.0.0 源码
12-08
rocketmq-dashboard 1.0.0 源码
基于Q-learning算法在能源市场中实现效益最大化研究（Matlab代码实现）
12-08
基于Q-learning算法在能源市场中实现效益最大化研究（Matlab代码实现）
AI时代，中小技术转移机构面临收入增长乏力挑战，如何抓住企业创新数智空间机遇实现体系化核心优势？.docx
12-08
聚焦AI+技术转移、院所成果转化与知识产权管理，以人工智能为底座的数智化科技创新平台，为提升区域科技管理与创新能力提供全面解决方案，驱动地方产业升级。
【智能无人系统】基于ACO-MLP混合模型的无人机三维路径规划： 项目介绍 MATLAB实现基于ACO-MLP 蚁群算法（ACO）结合多层感知机（MLP）进行无人机三维路径规划（含模型描述及部分示例代
最新发布
12-08
内容概要：本文介绍了一个基于MATLAB实现的无人机三维路径规划项目，采用蚁群算法（ACO）与多层感知机（MLP）相结合的混合模型（ACO-MLP）。该模型通过三维环境离散化建模，利用ACO进行全局路径搜索，并引入MLP对环境特征进行自适应学习与启发因子优化，实现路径的动态调整与多目标优化。项目解决了高维空间建模、动态障碍规避、局部最优陷阱、算法实时性及多目标权衡等关键技术难题，结合并行计算与参数自适应机制，提升了路径规划的智能性、安全性和工程适用性。文中提供了详细的模型架构、核心算法流程及MATLAB代码示例，涵盖空间建模、信息素更新、MLP训练与融合优化等关键步骤。; 适合人群：具备一定MATLAB编程基础，熟悉智能优化算法与神经网络的高校学生、科研人员及从事无人机路径规划相关工作的工程师；适合从事智能无人系统、自动驾驶、机器人导航等领域的研究人员； 使用场景及目标：①应用于复杂三维环境下的无人机路径规划，如城市物流、灾害救援、军事侦察等场景；②实现飞行安全、能耗优化、路径平滑与实时避障等多目标协同优化；③为智能无人系统的自主决策与环境适应能力提供算法支持； 阅读建议：此资源结合理论模型与MATLAB实践，建议读者在理解ACO与MLP基本原理的基础上，结合代码示例进行仿真调试，重点关注ACO-MLP融合机制、多目标优化函数设计及参数自适应策略的实现，以深入掌握混合智能算法在工程中的应用方法。
评论 2
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值