【AtCoder】【DP】【思维】 Salvage Robots(AG004)

最新推荐文章于 2024-07-11 09:27:54 发布

G20202502

最新推荐文章于 2024-07-11 09:27:54 发布

阅读量464

点赞数 2

CC 4.0 BY-SA版权

分类专栏： exams DP 思维题

本文链接：https://blog.youkuaiyun.com/G20202502/article/details/82767514

exams 同时被 3 个专栏收录

19 篇文章

订阅专栏

思维题

11 篇文章

订阅专栏

7 篇文章

订阅专栏

本文针对一个机器人救援问题，通过转换视角将机器人移动转化为出口移动，采用动态规划算法求解最多可救援的机器人数量。文章详细介绍了状态定义、状态转移过程及代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题意：

有一个n*m的矩阵，每一个格子中只会含有以下的字符：’.'表示位置为空，'o’表示这个位置有一个机器人，'E’表示这个位置为出口。保证出口只会出现一次。
现在你可以命令让所有的机器人同时向上或下或左或右移动一步。如果这个机器人掉出了矩阵，那么就无法营救这个机器人了，并且这个机器人会消失；如果这个机器人到达了Exit，那么它就被成功营救了，也会立即消失。
现在要你求经过上述操作后能够营救的机器人最多能有多少个。

数据范围：

1<=n,m<=100

思路：

这道题首先需要转化一下。原题中将机器人移上移下的操作看起来难以维护，那么我们可以考虑机器人与出口之间的相对位置，那么就可以转变为是出口在矩阵中跑来跑去，还带着一个固定大小的框，一旦在框外的机器人就会掉出矩阵。
那么这样子就可以来定义状态了。（这里借用一下官方题解的图）
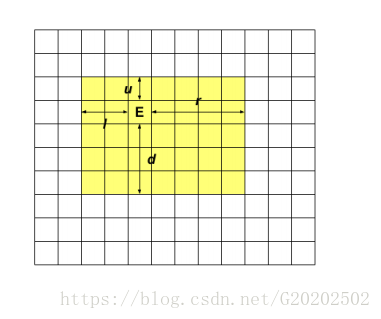
在这里插入图片描述
上面图片的黄色局域指的就是出口能够走到的所有的区域。
定义dp[l][r][u][d]为出口距离这个区域上边界的区域，距离这个区域下边界的区域，距离这个区域左边界的区域，距离这个区域右边界的区域。有可能会开不下，后面会详细解释。
那么这样子肯定有一些区域已经无法到达了：
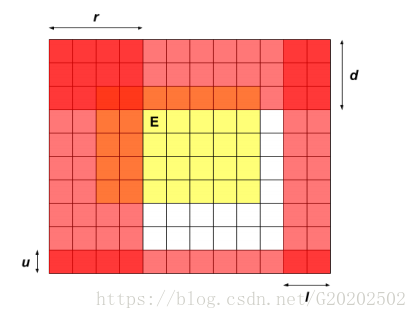
在这里插入图片描述
红色区域就是已经无法到达的区域。
对于白色的格子，是出口既没有到达过，也不会有机器人掉出矩阵的地方；
对于只有红色的格子，是机器人已经掉出矩阵，并且不会有出口到达的地方；
对于只有黄色的格子，是机器人已经被营救，并且也永远都不会掉出去的地方；
对于又有红色，又有黄色的格子，是出口能够到达，并且最终如果有机器人，也会掉出去的地方。那么对于这种格子，里面的机器人是否被营救是不确定的。
那么转移必然是对于白色格子进行的。
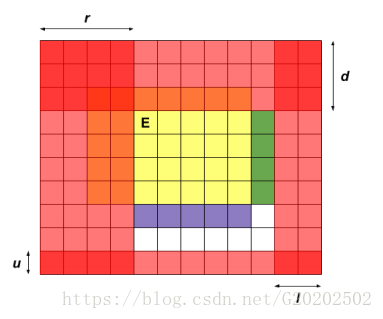
在这里插入图片描述
对于当前这个图而言，可以沿着紫色或者是绿色的区域进行转移。那么造成的效果在状态上体现出来就是d+1或者是r+1，在值体现出来就是加上紫色区域的机器人，或者是加上绿色区域的机器人。
也就是：
$d p [l] [r] [u] [d + 1] = d p [l] [r] [u] [d] + s u m [p u r p l e]$
$d p [l] [r + 1] [u] [d] = d p [l] [r] [u] [d] + s u m [g r e e n]$
当然对于一个状态来说，这样的转移可能并不是完全的，因为还有可能向着l+1或者是u+1的方向进行，只是这里被舍掉了而已，因为左边和上面没有白色的格子，是无法转移的。
对于sum[purple]和sum[green]的处理可以简单的对于每一行，每一列处理一个前缀和求出。
如果还有不懂的，可以看代码里面的解释：

#include<cstdio>
#include<cstring>
#include<algorithm>
#define MAXN 100
using namespace std;
char Map[MAXN+5][MAXN+5];
int n,m,ex,ey;
int sumr[MAXN+5][MAXN+5],sumc[MAXN+5][MAXN+5];
int dp[MAXN+5][MAXN+5][MAXN+5];
void Init()
{
	memset(dp,-1,sizeof(dp));
}
int main()
{
//	freopen("robot.in","r",stdin);
//	freopen("robot.out","w",stdout);
	Init();
	scanf("%d %d",&n,&m);
	for(int i=1;i<=n;i++)
	{
		scanf("%s",Map[i]+1);
		for(int j=1;j<=m;j++)
		{
		//对于每一行或每一列单独计算前缀和
			sumr[i][j]=sumr[i][j-1];
			sumc[i][j]=sumc[i-1][j];
			if(Map[i][j]=='E')
				ex=i,ey=j;
			else if(Map[i][j]=='o')
			{
				sumr[i][j]++;
				sumc[i][j]++;
			}
		}
	}
	int L,R,U,D,ans=0;
	//L,R,U,D表示最大的l,r,u,d能够达到的范围，也就是出口距离整个矩阵的上下左右的距离
	L=ey-1;
	R=m-ey;
	U=ex-1;
	D=n-ex;
	dp[0][0][0]=0;
	for(int l=0;l<=L;l++)
		for(int r=0;r<=R;r++)
			for(int u=0;u<=U;u++)
				for(int d=0;d<=D;d++)
				{
					if(dp[r][u][d]==-1)
						continue;
					ans=max(dp[r][u][d],ans);
					//这里的up,down,left,right是黄色区域的上下左右边界
					//因为向下走d步到达黄色区域的下边界，上面也会因为框的移动而产生出d的红色区域
					//那么就是说不含有红色的区域的上界就是d+1。而还有一种上界的可能就是ex向上走u步
					//也就是正常的黄色区域（ex-u）。
					//那么两者取一个交集，也就是含有黄色，并且不含有红色的区域就是max(ex-u,d+1)了
					//可以结合上面的图来看，之后的down,left,right也是一样的
					int up=max(ex-u,d+1);
					int down=min(ex+d,n-u);
					int left=max(ey-l,r+1);
					int right=min(ey+r,m-l);
					//红色区域将出口这最后一块圣土都吞并了，显然状态是非法的
					if(up>down||left>right)
						continue;
					int add;
					//u是上面的黄色区域的大小，U-d是上面的除掉红色区域之后的大小
					//如果u<剩余区域的大小，才能够有白色区域，后面同理
					if(u<U-d)
					{
						add=sumr[ex-u-1][right]-sumr[ex-u-1][left-1];
						dp[r][u+1][d]=max(dp[r][u+1][d],dp[r][u][d]+add);
					}
					if(d<D-u)
					{
						add=sumr[ex+d+1][right]-sumr[ex+d+1][left-1];
						dp[r][u][d+1]=max(dp[r][u][d+1],dp[r][u][d]+add);
					}
					if(r<R-l)
					{
						add=sumc[down][ey+r+1]-sumc[up-1][ey+r+1];
						dp[r+1][u][d]=max(dp[r+1][u][d],dp[r][u][d]+add);
					}
					if(l<L-r)
					{
						add=sumc[down][ey-l-1]-sumc[up-1][ey-l-1];
						dp[r][u][d]=max(dp[r][u][d],dp[r][u][d]+add);
					}
				}
	printf("%d\n",ans);
	return 0;
}

下面是卡内存的问题。有两种方法，一种是使用short int，还有一种是将[l]那一位省掉。
只需要保证在循环色最外层枚举l，在最后一步进行dp[l+1][r][u][d]的转移就可以了。这样子就可以保证后面dp[r][u][d]这个状态不会用来转移，存的值也就是dp[l+1][r][u][d]的值。上面的代码也是这样子实现的。