北大OJ

最新推荐文章于 2025-11-05 14:40:58 发布

原创最新推荐文章于 2025-11-05 14:40:58 发布 · 1.9k 阅读

0 ·

CC 4.0 BY-SA版权

数据结构与算法专栏收录该内容

22 篇文章

订阅专栏

本文详细解析了在棋盘上计算不同棋子从起点到终点的最短步数的算法，包括王、后、车和马的移动路径计算。通过减少讨论范围至四个主要方向，文章提供了具体的代码实现，展示了如何通过模拟每种棋子的移动特性来解决这一问题。

以前一直在九度OJ上做题，最近这个OJ登陆不上去，转到北大OJ做题，希望通过做题学习和熟悉一些常用的算法。

一.1657-distance on chessboard

这是一道比较简单的模拟题，只要分情况讨论，一一求解即可

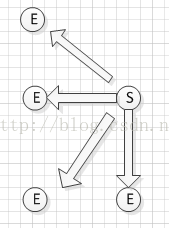
1 首先把起点到终点的方向定为西北、西、西南、南，由8个方向减少到4个方向。

2 考虑王的步数情况，分西北、西、西南、南四种情况考虑，对于西北方向，即终点在起点的左上方，则起点先沿西北方向走，当与终点平行的时候，再选择往西或者往东走到终点的位置，此时，走过的步数就是王的步数；对于西这个方向，直接从起点向西走到终点就是王的总步数；对于西南方向，则先沿西南方向走，当与终点平行的时候，再往西或者东走。对于正南方向则直接走向终点，即为总步数。

3 后和车的情况比较简单。

5 马只考虑西北和西南两个方向，假如终点在起点的左上方，则马往西北方向走，每走一步，判断终点是否在该点的西南或者东北方向；假如终点在起点的右下方，则马往西南方向走，没走一步，判断终点是否在该点的西北或者东南方向。

代码如下:

#include "stdio.h"
#include "math.h"
#include "stdlib.h"
int main(int argc, char **argv)
{
int t;
int i, j;
char start[10], end[10];
char temp, tmpStartX, tmpStartY, tmpEndX, tmpEndY;
int cnt;
int flag = 0;
scanf("%d", &t);
for (i = 0; i < t; i++)
{
flag = 0;
scanf("%s%s", start, end);
if (start[0] == end[0] && start[1] == end[1])//起点和终点重合
{
printf("0 0 0 0\n");
continue;
}
if (start[0] > end[0])//减少讨论范围，只考虑西北，西，西南，南四个方向
{
temp = end[0];
end[0] = start[0];
start[0] = temp;
temp = end[1];
end[1] = start[1];
start[1] = temp;
}
cnt = 0;
tmpStartX = start[0];
tmpStartY = start[1];
tmpEndX = end[0];
tmpEndY = end[1];
//王
if (start[0] != end[0])
{
if (start[1] < end[1])//西南方向
{
while (start[1] < end[1])
{
start[0]++;
start[1]++;
cnt++;
}
}
else if (start[1] > end[1])//西北方向
{
while (start[1] > end[1])
{
start[0]++;
start[1]--;
cnt++;
}
}
else//正西方向，什么都不做
{
}
flag = 1;
}
if (flag == 0)//正南方向
{
cnt += abs(start[1] - end[1]);
}
else
{
cnt += abs(start[0] - end[0]);
}
start[0] = tmpStartX;
start[1] = tmpStartY;
end[0] = tmpEndX;
end[1] = tmpEndY;
printf("%d ", cnt);
cnt = 0;
tmpStartX = start[0];
tmpStartY = start[1];
tmpEndX = end[0];
tmpEndY = end[1];
//后
if (start[0] == end[0] || start[1] == end[1]
|| abs(end[0] - start[0]) == abs(end[1] - start[1]))
{
printf("1 ");
}
else
{
printf("2 ");
}
//车
if (start[0] == end[0] || start[1] == end[1])
{
printf("1 ");
}
else
{
printf("2 ");
}
//马
int flag = 0;
if (abs(end[0] - start[0]) == abs(end[1] - start[1]))
{
printf("1\n");
}
else
{
while (start[0] <= 'h' && start[1] <= '8')
{
if (end[1] >= start[1])//西南方
{
start[0]++;
start[1]++;
}
else //西北方向
{
start[0]++;
start[1]--;
}
if (abs(end[0] - start[0]) == abs(end[1] - start[1]))
{
printf("2\n");
flag = 1;
break;
}
}
if (0 == flag)
{
printf("Inf\n");
}
}
}
return 0;
}