范数简介

概述

我们知道距离的定义是一个宽泛的概念，只要满足非负、自反、三角不等式就可以称之为距离。范数是一种强化了的距离概念，它在定义上比距离多了一条数乘的运算法则。有时候为了便于理解，我们可以把范数当作距离来理解。

在数学上，范数包括向量范数和矩阵范数，向量范数表征向量空间中向量的大小，矩阵范数表征矩阵引起变化的大小。一种非严密的解释就是，对应向量范数，向量空间中的向量都是有大小的，这个大小如何度量，就是用范数来度量的，不同的范数都可以来度量这个大小，就好比米和尺都可以来度量远近一样；对于矩阵范数，学过线性代数，我们知道，通过运算$AX=B$，可以将向量$X$变化为$B$，矩阵范数就是来度量这个变化大小的。

这里简单地介绍以下几种向量范数的定义和含义:

1、 L-P范数

与闵可夫斯基距离的定义一样，L-P范数不是一个范数，而是一组范数，其定义如下：
$Lp=\sqrt[p]{\sum _1^n{x}_i^p}，x=(x_1,x_2,\cdots ,x_n)$
根据P 的变化，范数也有着不同的变化，一个经典的有关P范数的变化图如下：

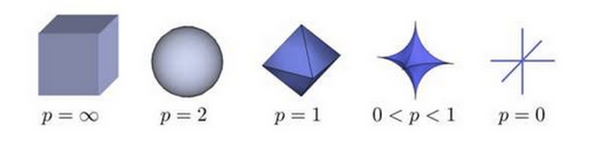
上图表示了p从无穷到0变化时，三维空间中到原点的距离（范数）为1的点构成的图形的变化情况。以常见的L-2范数（p=2）为例，此时的范数也即欧氏距离，空间中到原点的欧氏距离为1的点构成了一个球面。

实际上，在$\le p<1$时，Lp并不满足三角不等式的性质，也就不是严格意义下的范数。以p=0.5，二维坐标(1,4)、(4,1)、(1,9)为例，$\sqrt[0.5]{(1+\sqrt{4})}+\sqrt[0.5]{(\sqrt{4}+1)}<\sqrt[0.5]{(1+\sqrt{9})}$。因此这里的L-P范数只是一个概念上的宽泛说法。

2、L0范数

当P=0时，也就是L0范数，由上面可知，L0范数并不是一个真正的范数，它主要被用来度量向量中非零元素的个数。用上面的L-P定义可以得到的L-0的定义为：
$||x||=\sqrt[0]{\sum _1^n{x}_i^0}，x=(x_1,x_2,\cdots ,x_n)$
这里就有点问题了，我们知道非零元素的零次方为1，但零的零次方，非零数开零次方都是什么鬼，很不好说明L0的意义，所以在通常情况下，大家都用的是：

$||x|{|}_0=(i|x_i̸=0)$

表示向量$x$中非零元素的个数。
对于L0范数，其优化问题为：

$min||x|{|}_0$
$s.t.Ax=b$

在实际应用中，由于L0范数本身不容易有一个好的数学表示形式，给出上面问题的形式化表示是一个很难的问题，故被人认为是一个NP难问题。所以在实际情况中，L0的最优问题会被放宽到L1或L2下的最优化。

3、L1范数

L1范数是我们经常见到的一种范数，它的定义如下：

$||x|{|}_1={\sum }_i|x_i|$

表示向量$x$中非零元素的绝对值之和。
L1范数有很多的名字，例如我们熟悉的曼哈顿距离、最小绝对误差等。使用L1范数可以度量两个向量间的差异，如绝对误差和（Sum of Absolute Difference）：

$SAD(x_1,x_2)={\sum }_i|x_{1i}-x_{2i}|$

对于L1范数，它的优化问题如下：

$min||x|{|}_1$
$s.t.Ax=b$

由于L1范数的天然性质，对L1优化的解是一个稀疏解，因此L1范数也被叫做稀疏规则算子。通过L1可以实现特征的稀疏，去掉一些没有信息的特征，例如在对用户的电影爱好做分类的时候，用户有100个特征，可能只有十几个特征是对分类有用的，大部分特征如身高体重等可能都是无用的，利用L1范数就可以过滤掉。

4、L2范数

L2范数是我们最常见最常用的范数了，我们用的最多的度量距离欧氏距离就是一种L2范数，它的定义如下：

$||x|{|}_2=\sqrt{{\sum }_i{x}_i^2}$

表示向量元素的平方和再开平方。
像L1范数一样，L2也可以度量两个向量间的差异，如平方差和（Sum of Squared Difference）:

$SSD(x_1,x_2)={\sum }_i(x_{1i}-x_{2i}{)}^2$

对于L2范数，它的优化问题如下：

$min||x|{|}_2$
$s.t.Ax=b$

L2范数通常会被用来做优化目标函数的正则化项，防止模型为了迎合训练集而过于复杂造成过拟合的情况，从而提高模型的泛化能力。

5、$L-\infty$范数

当$P=\infty$时，也就是$L-\infty$范数，它主要被用来度量向量元素的最大值。用上面的L-P定义可以得到的$L-\infty$的定义为：

$||x|{|}_{\infty }=\sqrt[\infty ]{\sum _1^n{x}_i^{\infty }}，x=(x_1,x_2,\cdots ,x_n)$

与L0一样，在通常情况下，大家都用的是：

$||x|{|}_{\infty }=max(|x_i|)$

来表示$L-\infty$

参考：
https://blog.youkuaiyun.com/shijing_0214/article/details/51757564