百面机器学习之 K-Means聚类

最新推荐文章于 2024-08-28 15:25:23 发布

Francis_s

最新推荐文章于 2024-08-28 15:25:23 发布

阅读量2.7k

点赞数

分类专栏：百面机器学习文章标签：聚类机器学习 kmeans

本文链接：https://blog.youkuaiyun.com/Francis_s/article/details/121731586

版权

百面机器学习专栏收录该内容

11 篇文章

订阅专栏

本文详细介绍了非监督学习中的K-Means聚类算法，包括其基本思想、步骤、优缺点及改进方法。K-Means通过迭代寻找数据最优分割，但在初始值敏感、局部最优和数据分布不均衡等问题上存在局限。为改善这些问题，提出了数据预处理、动态调整K值、使用K-Means++选择初始中心和动态添加删除类别等策略。此外，还讨论了评估聚类算法的方法，如轮廓系数、均方根标准偏差等。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1. 非监督学习

主要包含两大类学习方法：数据聚类和特征变量关联，这里只讲数据聚类的方法，也就是K-Means，它是通过多次迭代找到数据的最优分割。

和监督学习不同的是，监督学习是知道了样本label，也就是知道了样本是属于哪个类的，所以模型/网络只需要对某一类建立自己学习到的规则就好了，然后对于未知的样本根据我们先验学习到的规则进行分类。

而这里的聚类（K-Means），是在事先不知道任何样本类别的情况下，通过数据间的内在关系把样本划分为若干类别，使得同类样本之间的样本相似度高，不同样本之间的样本相似度低。

2. K-Means

K-Means的基本思想就是通过迭代方式寻找K个簇，使得聚类结果对应的cost function最小，一般来说，我们定义K-Means的Cost function是通过各个样本距离所属簇中心点的误差平方和来定义的：

$J(c.\mu) = \sum^M_{i=1}\left \| x_i-\mu_{ci} \right \|^2$

2.1 简述K-Means算法的具体步骤

首先明确核心的目标，就是在给定的数据集内，我们将这个数据集划分成K个簇，并给出每个数据对应的簇中心点（也就是给出对应每个样本所属类别）：

1. 数据预处理，归一化，离群点筛选

2. 随机选取K个簇的中心，记为: $\mu_1^{0},\mu_2^{0},\mu_3^{0},...,\mu_K^{0}$ （0上标指的是第一代）

3. 定义cost function： $J(c.\mu) = min\sum^M_{i=1}\left \| x_i-\mu_{ci} \right \|^2$

4. 重复执行以下步骤，直到cost function 收敛

对每一个样本 $X_i$ ，将其分配到距离最近的簇。

然后对每一个簇，现在不是有新的点了嘛，就重新计算该簇的中心。

PS：有重要的点就是

咱们一开始是随机选择K个点作为初始的簇。（这些点一般都是从数据集中随机抽取的，这里会大大影响到聚类的结果）

计算簇的中心是根据当前每个簇的所有点的平均值去计算的

2.2 K-Means的优缺点是啥

K-Means的主要缺点是

1. 受初值和离群点的影响，使得每次的结果不稳定

2. 结果通常不是全局最优而是局部最优，

3. 无法很好地解决数据簇分布差别较大的情况（数量悬殊）

4. 需要人工设置初始K值

K-Means的主要优点是

1. 计算效率还是比较高效的

所以根据他的缺点，我们去给它做一个改进：

1. 数据归一化和离群点处理

K-Means 是根据欧式距离去计算额度，所以均值和方差大的数据会对聚类的结果产生很大的影响，也就是之前说过的量纲不一样。所以我们要做归一化。

离群点或者噪声也会对均值产生很大的影响，这会影响到后面更新簇中心位置，导致中心偏移，因此要对离群点做一下过滤

2. 合理选择K值

K值（划分多少个簇）选太少，那就会造成Loss变大，K值选太大了，那就有一些簇是多余的，完全可以做合并，于是K值的选择成为一个比较棘手的问题了。书上给出的K值的选择一般是基于多次实验结果得到的，也就是书上说的《手肘法》，其实换句话说就是看拐点

另外一个方法就是Gap Statistic，只需要直接找到最大的Gap Statistic对应K值就好了

下面来看 Gap Statistic的定义：

$Gap(K) = E(logD_k) - logD_k$

其中 $E(logD_k)$ 是 $logD_k$ 的期望，一般是通过蒙特卡洛模拟产生的。（这里应该补一下各种采样方法）

然后在样本所在的区域按照均匀分布随机产生和原始样本数一样多的随机样本，并对这个随机样本(注意噢，这里是单个样本)做K-Means，得到一个 $D_k$ ，重复多次可以计算出 $E(logD_k)$ 的近似值了

其中 $D_k$ 就是当分为K个簇时，对应的损失函数记为 $D_k$

$Gap(k)$ 的物理含义就是随机样本的损失与实际样本的损失之差。假如实际样本对应的最佳簇数是k，那么实际样本的损失应该很小，随机样本损失与实际样本损失之差会达到最大的才对，于是我们选择K就等同于在 Gap(K) 取最大值对应的K了。

3. 改进初始值K选择簇点

K-Means在最开始是随机选取数据集中K个点作为聚类的K个聚类中心，这引入K-Means++ 按照以下的思想去选取不同K个聚类中心：

假设已经选去了N个初始聚类中心，在选第n+1个的时候，距离当前n个聚类中心越远的点约有更高的概率被选择为第n+1个聚类中心。

这个选取的方法符合聚类的初衷：希望类内的距离越近越好，类间的距离越远越好

4. 动态调整K值

这里引入一个叫ISODATA的方法。

很多时候我们都无法对K值做一个比较合理的假设，于是我们就想让模型来自己做假设，于是这里就涉及到了K的添加和删除的问题了。

ISODATA模型的思想：

合并操作：当某个类别的样本数过少时，模型就把这个类别给去掉

分裂操作：当某个类别的样本过多，分散程度比较大，就把该类分为两个子类

所以我们需要一些阈值（参数）来让模型知道什么时候做合并，什么时候做分裂，这就需要提前设定参数了：

1. 预期聚类个数：这个是用户指定的参考值，但是最终的结果不是靠这个指标决定的，这个指标只是给出了一个大概范围，最终的K会落在 1/2*K到2K之间。

2. 每个类要求的最少样本数目：如果分类后某一个类里面的样本数目小于该阈值，就不做该分裂

3. 最大方差sigma，就是来衡量当前这个类里面的样本分布是不是很分散的，如果超过该阈值，就要做分类。这里面我觉得可以和信息熵联系起来

4. 两个类之间的最小距离：这个就是用来衡量是不是要合并了，小于该阈值的话，就要对这两个类做一个合并操作

5. 采用核函数去做一个映射

为什么需要一个核函数去映射呢？因为K-Means本质上是假设了各个数据簇具有一样的先验概率，假设数据簇都服从球形分布，但是这种假设肯定是不合理的，在生活当中不常见，所以我们要将引入核函数，来对原始数据做一个非线性的映射，将输入空间的数据点映射到高维度的特征空间，在新的特征空间里面做聚类分析。

2.3 K-Means是EM 的特例

但是从书上的角度来说，这个K-Means其实是EM算法的一个体现。当初一看有点懵逼，看到后面才知道，原来K-means是EM算法的特例

K-Means问题：给定数据点 $x_1,x_2,...,x_N$ ，给定分类数目K，求出K个簇的各自中心 $\mu_1,\mu_2,...,\mu_K$ ，使得所有点到各自的簇的中心的距离的平方和是最小的：

$J(c.\mu) = min\sum^M_{i=1}\left \| x_i-\mu_{ci} \right \|^2$

含隐变量的最大似然问题：给定数据点 $x_1,x_2,...,x_N$ ，给定分类数目K，考虑下面的这个含有隐变量的最大似然问题（生成模型）：（什么是生成式模型）

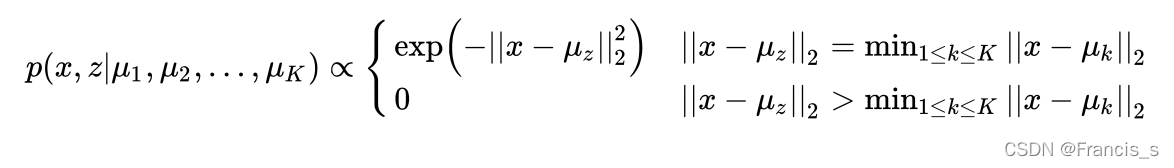
其中 z 就是隐变量，这个公式的意义即使，对于某个将要生成的样本x 和z，如果不满足x到簇中心 $\mu_z$ 的距离小于等于x到簇中心的距离，那就不生成这个点。如果满足，z 就取这个最近的簇的编号（如果刚好有多个都一样近，那就均匀分布地取一个簇），然后以高斯的概率密度函数在这个类中心周围生成这个样本点x。

EM其实就是先求Expect，再求Max啊

E步：求得当前簇下，所有点 $x_i$ 对应的最近的簇 $\mu_z$

M步：也是套用EM的公式，然后对argmax进行转换，把求最大值转换为求最小值：

变成求 $\sum^M_{i=1} \left \| x_i-\mu_z_{i} \right \|^2$ 的最小值

正如书上说的，M步其实就是在根据E步分配到簇去计算距离，并且去更新每一个簇的点。从而达到每一次cost function越来越小，在M步这里达到收敛。

2.4 证明K-Means是收敛的

这里面提到了EM收敛的原因，所以这里就不证明了。

3. 聚类算法的评估

3.1 以聚类问题为例，假设没有外部标签数据，如何评估两个聚类算法的优劣呢？

为了评估不同聚类算法的优劣，需要了解常见数据簇的特点：

A. 以重新定义的数据簇：该类数据倾向于球形分布，也就是K-Means的假设数据粉步，通常中心被定义为质心（所有数据的平均值），集合中的数据到中心的距离相比其他簇中心的距离更近

B. 以密度定义的数据簇：该类的数据集合呈现和周围数据簇明显不同的密度，当数据簇不规则或者相互缠绕的时候，并且噪声和离群点都在里头很难去除的时候。就用基于密度的簇去定义

C. 以连通定义的数据簇：簇内的元素之间有连接关系，整个数据簇表现为图结构，对于不规则的数据簇就非常有效

D. 以概念定义的数据簇：簇内所有数据点具有某种共同性质

因为不同数据的分布我们就应该用不同的簇分类方法去定义他们

聚类的评估是估计在数据集上进行聚类的可行性，以及聚类方法产生结果的质量。

1. 估计聚类的趋势

检测数据分布中是否存在非随机的簇结构。如果数据是随机的，那么聚类的结果也是毫无意义的

A. 怎么看是不是随机的呢。可以观察聚类的误差是否随聚类类别数量的增加而单调变化，如果数据是随机的，那么聚类的误差随着聚类K的数量上升而变化不大，也就是说找不到一个合适的K来去对这堆数据做区分。

B. 可以用霍普金斯统计量来判别数据在空间上的随机性。

2. 判定数据簇的数量K

上面咱们说过的一个是手肘法，人工去做不同K的Loss图走势，选定一个最大的，还有一个方法是Gap Statistic方法。

3. 评估聚类的质量

在无监督的情况下，我们可以通过考察簇的分离情况，紧凑情况来评估聚类的效果。

A. 轮廓系数

给定一个点 $p$

$a(p)$ 是点p与同一簇中其他点之间的平均距离：反应是p所在簇中的紧凑程度

$b(p)$ 是点p与另一个不同簇（与点p最接近的簇）中的点之间的最小平均距离。反应的是该簇与其他簇的分离程度

所在最终我们会对所有点的轮廓系数进行加何求平均处理来反应当前聚类的质量

当前点p的轮廓系数公式：

$s(p) = \frac{b(p)-a(p)}{max \left \{ a(p),b(p) \right \} }$

B. 均方根标准偏差

用来衡量一个聚类结果的同质性，也就是紧凑程度。但是我从公式上看不出一个具体的表现形式出来。书上说可以把这个指标看作是经过归一化的标准差。但真的看不出来是在干嘛

C. R方

用来衡量一个聚类的差异度：

$R \_ Square = \frac{\sum_{x \in D}\left \| x-c \right \|^2 - \sum_i \sum_{x \in C_i} \left \| x-c_i \right \|^2 }{\sum_{x \in D}\left \| x-c \right \|^2}$