深度学习中不同的Normalization方法的比较

不同的Normalization方法的比较

深度学习中常用的Normalization方法有Batch Normalization（BN，2015）、Layer Normalization（LN，2016）、Instance Normalization（IN，2017）、Group Normalization（GN，2018）。

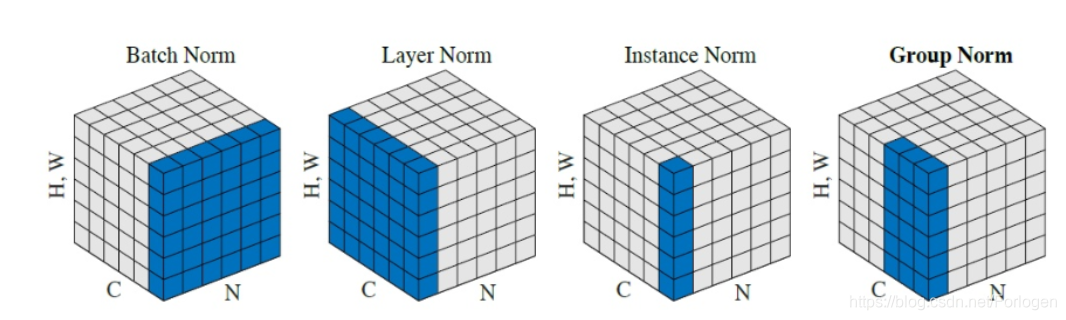
不同的Normalization层的输入为特征图（Feature Map），通常记为[N,C,H,W]，：

• N：批次大小
• C：通道数
• H：高度
• W：宽度

不同的方法的区别可简单的归结为：

• BN是在batch上，对N、H、W做归一化，而保留通道 C 的维度。BN对较小的batch size效果不好。BN适用于固定深度的前向神经网络，如CNN，不适用于RNN
• LN在通道方向上，对C、H、W归一化，主要对RNN效果明显
• IN在图像像素上，对H、W做归一化，用在风格化迁移
• GN将channel分组，然后再做归一化

形象化的表述：如果把特征图$x\in R^{N\times C\times H\times W}$ 比喻成一摞书，这摞书总共有 N 本，每本有 C 页，每页有 H 行，每行 有W 个字符。

• BN 求均值时，相当于把这些书按页码一一对应地加起来（例如第1本书第36页，第2本书第36页…），再除以每个页码下的字符总数：N×H×W，因此可以把 BN 看成求“平均书”的操作（注意这个“平均书”每页只有一个字），求标准差时也是同理。
• LN 求均值时，相当于把每一本书的所有字加起来，再除以这本书的字符总数：C×H×W，即求整本书的“平均字”，求标准差时也是同理。
• IN 求均值时，相当于把一页书中所有字加起来，再除以该页的总字数：H×W，即求每页书的“平均字”，求标准差时也是同理。
• GN 相当于把一本 C 页的书平均分成 G 份，每份成为有 C/G 页的小册子，求每个小册子的“平均字”和字的“标准差”。

Batch Normalization

BN解决的问题：

• 在深度神经网络中使用mini-batch SGD进行训练时，由于不同的批次的数据所满足的分布可能是不同的，导致模型的训练极其困难；
• Internal Covariate Shift，ICS问题：训练过程中，激活函数会改变各层数据的分布，随着网络的加深，这种改变会越来越明显，是的模型训练困难，收敛速度下降，甚至出现梯度消失的问题

BN的主要思想在于：对于每一个神经元来说，在数据进入激活函数前，沿着通道计算每个批次的均值和方差，使得每一批次的数据服从均值为０、方差为１的正态分布。

BN计算过程：

• 沿着通道计算每个批次的均值$\mu$：$\mu =\frac{1}{m}{\sum }_{i=1}^m{z}^{(i)}$

• 沿着通道计算每个批次的方查$\sigma$：${\sigma }^2=\frac{1}{m}{\sum }_{i=1}^m(z^{(i)}-\mu {)}^2$

• 归一化：$z_{Norm}^{(i)}=\frac{z^{(i)-\mu }}{\sqrt{{\sigma }^2+ϵ}}$

• 加入缩放和平移量$\gamma$和$\beta$：${\tilde{z}}^{(i)}=\gamma z_{Norm}^{(i)}+\beta$

BN优点：

• 允许较大的学习率；

• 减弱对初始化的强依赖性

• 保持隐藏层中数值的均值、方差不变，让数值更稳定，为后面网络提供坚实的基础；

• 有轻微的正则化作用

BN不足：

• 如果批次太小，计算的均值和方差不足以代表整个数据分布
• 如果批次太大，可能会超过内存容量，导致训练时间变长

Layer Normalization

LN对所有神经元的输入进行正则化操作，对于特征图来$x\in R^{N\times C\times H\times W}$来说，LN对每个样本的$C、H、W$维度上的数据求均值和标准差，保留$N$维度。
$$\begin{gathered} {\mu }_n(x)=\frac{1}{CHW}\sum _{c=1}^C\sum _{h=1}^H\sum _{w=1}^W{x}_{nchw} \\ {\sigma }_n(x)=\sqrt{\frac{1}{CHW}\sum _{c=1}^C\sum _{h=1}^H\sum _{w=1}^W(x_{nchw}-{\mu }_n(x){)}^2+ϵ} \end{gathered}$$
LN的优点在于不需要批训练，在单条数据内部就可以归一化，在RNN上效果明显，但在CNN上不如BN。

Instance Normalization

IN最初用于图像风格化，只对$H、W$做归一化，加速模型收敛，并保持每个图像实例之间的独立。对于对于特征图来$x\in R^{N\times C\times H\times W}$来说，IN对每个样本的$H、W$维度的数据求均值和标准差，保留$N、C$维度，即只在channel内部求均值和标准差。
$$\begin{gathered} y_{tijk}=\frac{x_{tijk}-{\mu }_{ti}}{\sqrt{{\sigma }_{ti}^2}+ϵ} \\ {\mu }_{ti}=\frac{1}{HW}\sum _{l=1}^W\sum _{m=1}^H{x}_{tilm} \\ {\sigma }_{ti}^2=\frac{1}{HW}\sum _{l=1}^W\sum _{m=1}^H(x_{tilm}-m{u}_{ti}{)}^2 \end{gathered}$$

Group Normalization

GN是为了解决BN对较小的批次效果差的问题，它适用于占用显存比较大的任务，GN独立于批次大小，它是LN和IN的折中。

GN的主要思想是把每一个样本的feature map的channel分为G组，每组有C/G个channel，然后对这些channel中的元素求均值和标准差，各组channel勇气对应的归一化参数独立地归一化。
$$\begin{gathered} {\mu }_{ng}(x)=\frac{1}{(C/G)HW}\sum _{c=gC/G}^{(g+1)C/G}\sum _{h=1}^H\sum _{w=1}^W{x}_{nchw} \\ {\sigma }_{ng}(x)=\sqrt{\frac{1}{(C/G)HW}\sum _{c=gC/G}^{(g+1)C/G}\sum _{h=1}^H\sum _{w=1}^W(x_{nchw}-{\mu }_{ng}(x){)}^2+ϵ} \end{gathered}$$

常用的 Normalization 方法：BN、LN、IN、GN

BatchNormalization、LayerNormalization、InstanceNorm、GroupNorm简介

Conditional Batch Normalization

传统的BN的公式为$y=\frac{x-E[x]}{\sqrt{\text{Var}[x]+ϵ}}\cdot \gamma +\beta$，其中$\gamma$和$\beta$为网络层的参数，需要通过BP学习。

CBN中也需要对输入的feature先减均值，再除以标准差，但是做线性映射时，所乘的缩放因子为${\gamma }_{pred}$，加的偏置为${\beta }_{pred}$，其中它们是将feature输入到MLP中前向传播得到的，而不需要模型通过BP学习。由于${\gamma }_{pred}$和${\beta }_{pred}$均依赖于输入的feature，因此这样的方式称为Conditional Batch Normalization。

CBN出现于《Modulating early visual processing by language》一文中

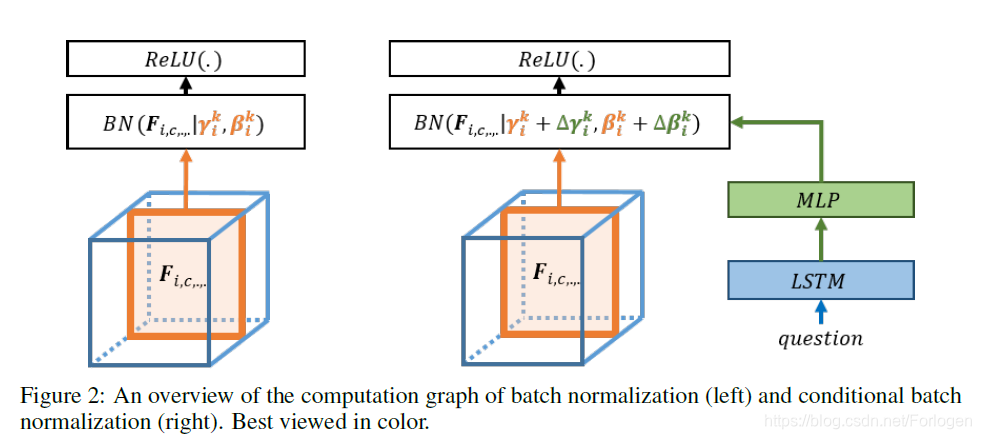
具体内容可见论文及下面的参考资料。

import torch.nn as nn
import torch.nn.functional as F
from torch.nn import init


class ConditionalBatchNorm2d(nn.BatchNorm2d):

    """Conditional Batch Normalization"""

    def __init__(self, num_features, eps=1e-05, momentum=0.1,
                 affine=False, track_running_stats=True):
        super(ConditionalBatchNorm2d, self).__init__(
            num_features, eps, momentum, affine, track_running_stats
        )

    def forward(self, input, weight, bias, **kwargs):
        self._check_input_dim(input)

        exponential_average_factor = 0.0

        if self.training and self.track_running_stats:
            self.num_batches_tracked += 1
            if self.momentum is None:  # use cumulative moving average
                exponential_average_factor = 1.0 / self.num_batches_tracked.item()
            else:  # use exponential moving average
                exponential_average_factor = self.momentum

        output = F.batch_norm(input, self.running_mean, self.running_var,
                              self.weight, self.bias,
                              self.training or not self.track_running_stats,
                              exponential_average_factor, self.eps)
        
        # 使feature map和 out的维度相同
        if weight.dim() == 1:
            weight = weight.unsqueeze(0)
        if bias.dim() == 1:
            bias = bias.unsqueeze(0)
        size = output.size()
        weight = weight.unsqueeze(-1).unsqueeze(-1).expand(size)
        bias = bias.unsqueeze(-1).unsqueeze(-1).expand(size)
        return weight * output + bias


class CategoricalConditionalBatchNorm2d(ConditionalBatchNorm2d):

    def __init__(self, num_classes, num_features, eps=1e-5, momentum=0.1,
                 affine=False, track_running_stats=True):
        super(CategoricalConditionalBatchNorm2d, self).__init__(
            num_features, eps, momentum, affine, track_running_stats
        )

        # 设置两个网络层，将图像的label转换为dense向量
        # nn.Embedding(num_calsses,num_features)
        # num_classes：类别数
        # num_features：特征向量的维度
        self.weights = nn.Embedding(num_classes, num_features)
        self.biases = nn.Embedding(num_classes, num_features)

        # 初始化self.weights和self.biases
        self._initialize()

    def _initialize(self):
        init.ones_(self.weights.weight.data)
        init.zeros_(self.biases.weight.data)

    # 这里c为LongTensor形式
    def forward(self, input, c, **kwargs):
        # 根据c挑选出weights embedding和biases embedding层中的第c行，做为weight和bias输入基类的前向传播函数
        weight = self.weights(c)
        bias = self.biases(c)

        # 得到Conditional Batch Normalization的输出
        return super(CategoricalConditionalBatchNorm2d, self).forward(input, weight, bias)

具体可查阅 ：Conditional Batch Normalization 详解 ，博主写的很详细

CBN在Self-Attention GAN 中的应用

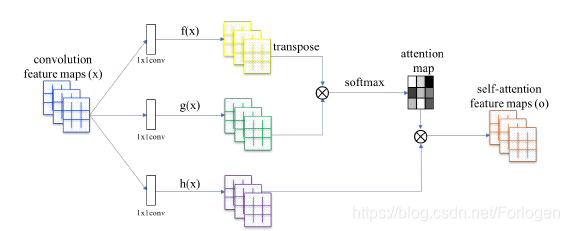
首先同通过卷积网络的隐藏层得到卷积的特征图（convolution feature maps）$x$，然后通过$1\times 1$的卷积核得到两个特征空间（feature space）$f=W_{f}x$和$g=W_{g}x$，然后使用$f$ 和 $g$ 来计算注意力，公式如下所示$${\beta }_{j,i}=\frac{\exp \left(s_{ij}\right)}{{\sum }_{i=1}^N\exp \left(s_{ij}\right)},\text{ where }{s}_{ij}=f{\left(x_i\right)}^{T}g\left(x_j\right)$$
其中${\beta }_{j,i}$表示在生成第$j$个区域的图像时对于第$i$个位置局部的注意力，然后将结果经过softmax归一化得到注意力图（attention map）。接着使用得到的注意力图和通过另一个$1\times 1$卷积核得到的特征空间计算得到注意力层的输出$\text{o}=(o_1,o_2,...,o_j,...,o_N)$，其中$o_j$ 计算为
$$o_j=\sum _{i=1}^N{\beta }_{j,i}h\left(x_i\right),\text{ where }h\left(x_i\right)=W_h{x}_i$$

上述的三个权重矩阵$W_f、W_g、W_h$需通过训练学习。最后将注意力层的输出和$x$进行结合，得到最终的输出$y_i=\gamma {\mathbf{o}}_{\mathbf{i}}+{\mathbf{x}}_{\mathbf{i}}$，其中$\gamma$初始设置为0，使得模型可以从简单的局部特征学起，逐渐学习到全局。

 def forward(self,x):
        """
            inputs :
                x : input feature maps( B X C X W X H)
            returns :
                out : self attention value + input feature 
                attention: B X N X N (N is Width*Height)
        """
        m_batchsize,C,width ,height = x.size()
        proj_query  = self.query_conv(x).view(m_batchsize,-1,width*height).permute(0,2,1) # B X CX(N)
        proj_key =  self.key_conv(x).view(m_batchsize,-1,width*height) # B X C x (*W*H)
        energy =  torch.bmm(proj_query,proj_key) # transpose check
        attention = self.softmax(energy) # BX (N) X (N) 
        proj_value = self.value_conv(x).view(m_batchsize,-1,width*height) # B X C X N

        out = torch.bmm(proj_value,attention.permute(0,2,1) )
        out = out.view(m_batchsize,C,width,height)
        
        out = self.gamma*out + x
        return out,attention

CBN在《cGANs With Projection Discriminator》中的应用

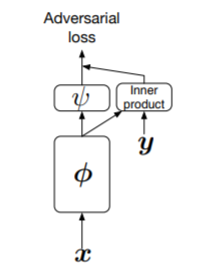
输入图片首先经过网络$\varphi$提取特征，然后把特征分成两路：一路与经过编码的类别标签 y 做点乘，另一路再通过网络$\varphi$映射成一维向量。最后两路相加，作为神经网络最终的输出。注意这个输出类似于 W-GAN，不经过 sigmoid 函数映射，越大代表越真实。

def forward(self, x, y=None):
        h = x
        h = self.block1(h)
        h = self.block2(h)
        h = self.block3(h)
        h = self.block4(h)
        h = self.block5(h)
        h = self.activation(h)
        # Global pooling
        h = torch.sum(h, dim=(2, 3)) # 提取x特征，送入两路，一路判断是否真实，一路判断是否属于label类
        output = self.l6(h) # 相当于 vanilla GAN, 判断 x 是否真实
        if y is not None:
            #  相当于不加 softmax 的 classifier, 直接提取 classifier 在 label 对应的维度的输出
            class_out = torch.sum(self.l_y(y) * h, dim=1, keepdim=True)
            # 把两部分加起来作为 discriminator 的 output
            output += class_out

        return output