蒙特卡罗方法初识

蒙特卡洛方法（Monte Carlo method，MC）在二十世纪四十年代由冯-诺伊曼、乌拉姆和尼古拉斯率先提出，名字来源于摩纳哥著名的赌城-蒙特卡洛。MC是一种通过生成合适的随机数和观察部分服从一些特定性质或属性的数据来解决问题的方法，通过统计抽样实验给各种各样的数学问题提供了近似解，这种方法对于一些太复杂以至很难分析求解的问题得到数字解法是非常有效的，而且同时适应于毫无概率性的问题 和 内在固有概率结构的问题。

但MC并不是某一种具体算法的名称，它是对一类随机算法的特性的概括。通常可以将随机算法分为两类：

• Las Vegas算法：精确的返回一个正确答案或是返回算法失败，采样次数越多，越有机会找到最优解
• MC：返回具有随机大小错误的答案，它是一个近似解，采样次数越多，越近似最优解

如何理解两种方法的差异呢？在蒙特卡罗算法是什么？中有一个很通俗易懂的例子。

• 假设现在有100个苹果，人只能蒙眼每次拿一个，挑出最大的。再随机拿1个跟它比，留下大的，再随机拿1个……每拿一次，留下的苹果都至少不比上次的小。拿的次数越多，挑出的苹果就越大，但除非拿100次，否则无法肯定挑出了最大的。这个挑苹果的算法，就属于蒙特卡罗算法——尽量找好的，但不保证是最好的
• 假如有一把锁，给100把钥匙，只有1把是对的。于是每次随机拿1把钥匙去试，打不开就再换1把。试的次数越多，打开（最优解）的机会就越大，但在打开之前，那些错的钥匙都是没有用的。这个试钥匙的算法，就是拉斯维加斯算法——尽量找最好的，但不保证能找到

蒙特卡洛方法最简单的一个例子就是求解圆周率$\pi$，假设在正方形内嵌一个半径为$r$的圆如下所示：

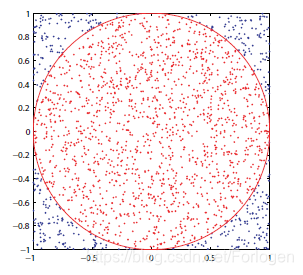
从公式推导上有$\frac{A_{\text{ circle }}}{A_{\text{ square }}}=\frac{\pi r^2}{4r^2}=\frac{\pi }{4}$，为了求解$\pi$可以随机的在正方形内选择$n$个点，那么落在圆内的点可能有$m$个，根据比例有$\frac{A_{\text{ circle }}}{A_{\text{ square }}}=\frac{m}{n}$，那么如果采样点的数目足够多时，$\frac{m}{n}$的值就会等于$\frac{\pi }{4}$，因此有$\pi =4\times \frac{m}{n}$。

另一个例子便是求积分，这里不再赘述，有兴趣的可看一下蒙特卡洛求定积分。

在现实的很多问题中我们往往无法得到一个精确解，那么常用的一种方法便是进行采样计算逼近于精确解的近似解。例如当无法精确的计算积分时，就把它看做是某分布下的期望，然后通过估计对应的平均值来近似期望。假设所需求解的期望为$s={\sum }_{\mathbf{x}}p(\mathbf{x})f(\mathbf{x})=E_p[f(\mathbf{x})]$，我们就可以从$p$在随机的抽取$n$个点，通过计算一个经验平均值来近似$s$.$${\hat{s}}_n=\frac{1}{n}\sum _{i=1}^{n}f\left({\mathbf{x}}^{(i)}\right)$$其中$p$是关于$x$的概率分布。而且得到的$\hat{s}$具有如下的性质：

• $\hat{s}$的估计是无偏的：$\mathbb{E}\left[{\hat{s}}_n\right]=\frac{1}{n}{\sum }_{i=1}^n\mathbb{E}\left[f\left({\mathbf{x}}^{(i)}\right)\right]=\frac{1}{n}{\sum }_{i=1}^{n}s=s$
• 由大数定理可知，如果$x^{(i)}$满足独立同分布，那么其平均值必然收敛到期望值：${\lim }_{n\to \infty }{\hat{s}}_n=s$
• 只要$Var[f(x^{(i)})]$有界，当$n$增大时，$Var[\widehat{s_n}]$就会减小并收敛至0：$$\begin{array}{rl}\mathrm{Var}\left[{\hat{s}}_n\right]& =\frac{1}{n^2}\sum _{i=1}^n\mathrm{Var}[f(\mathbf{x})]\\ & =\frac{\mathrm{Var}[f(\mathbf{x})]}{n}\end{array}$$
• 根据中心极限定理可知，$\widehat{s_n}$的分布将收敛到以$s$为均值、$\frac{Var[f(x)]}{n}$为方差的正态分布

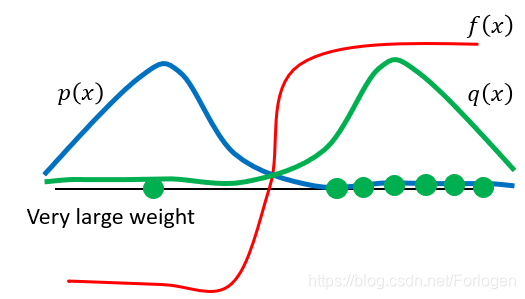
在蒙特卡洛方法中一个很重要的东西就是重要性采样（Importance Sampling）。它是使用一种分布来逼近所求分布的一种方法。假设我们想要求取目标分布$p$下的函数$f(x)$所满足的分布，如果$p$可以直接采样，那么使用蒙特卡洛方法有如下的计算$$E_{x\sim p}[f(x)]={\int }_{x}p(x)f(x)d_x\approx \frac{1}{N}\sum _{x_i\sim p,i=1}^{N}f\left(x_i\right)$$ 但是如果无法直接对$p$进行采样，那么上面的方法就不能使用了，这时就可以使用可以进行采样的分布$q$来近似$p$，计算公式为$$E_{x\sim p}[f(x)]={\int }_{x}p(x)f(x)d_x=E_{x\sim p^{\prime }}\left[\frac{p}{p^{\prime }}f(x)\right]\approx \frac{1}{N}\sum _{x_i\sim p^{\prime },i=1}^N\frac{p(x)}{p(x{)}^{\prime }}f(x)$$而且这里使用的分布$q$不应该和$p$相差太大，直观上我们可以理解所用分布自然不能和所要逼近的分布有太大的差距，否则就无法说的通了。下面从均值和方差的角度来看一下为什么要这样，从上面的式子中可以看出$E_{x\sim p}[f(x)]=E_{x\sim q}\left[f(x)\frac{p(x)}{q(x)}\right]$，它们的均值不会有太大差别。将两者的方差写为${\mathrm{Var}}_{x\sim p}[f(x)]$和${\mathrm{Var}}_{x\sim q}\left[f(x)\frac{p(x)}{q(x)}\right]$，根据概率论中方差和均值的转换公式有$$\begin{array}{l}{\mathrm{Var}}_{x\sim p}[f(x)]=E_{x\sim p}\left[f(x{)}^2\right]-{\left(E_{x\sim p}[f(x)]\right)}^2\\ {\mathrm{Var}}_{x\sim q}\left[f(x)\frac{p(x)}{q(x)}\right]=E_{x\sim q}\left[{\left(f(x)\frac{p(x)}{q(x)}\right)}^2\right]-{\left(E_{x\sim q}\left[f(x)\frac{p(x)}{q(x)}\right]\right)}^2\\ =E_{x\sim p}\left[f(x{)}^2\frac{p(x)}{q(x)}\right]-{\left(E_{x\sim p}[f(x)]\right)}^2\end{array}$$从中可以看出如果两者相差太大，就会导致$\frac{p(x)}{q(x)}$的值太大或是太小，从而导致两个分布之间的差别太大。下面通过图像可视化的理解以下上述的问题，蓝色实线表示分布$p(x)$，绿色实线表示真实采样的分布$q(x)$。从图中可以看出两者的分布是相反的，如果使用这样的$q(x)$去逼近$p(x)$，$q(x)$在右面奖励为正的部分采样的概率更大，因此大部分情况下奖励值均是大于零的，可能会在左边采样导致结果符合真实情况，但是因为概率太小，要达到这样的结果往往需要采样很多次，这样耗费的时间将会很多，因此两者之间的差别不应该太大。

在重要性采样中可知，理论上可以使用任意的$q(x)$来近似$p(x)$，只要两者间的差别不是很大即可。但有时一个满足要求的$q(x)$是不易找到的，这时就可以采用另外一个工具马尔可夫链蒙特卡罗方法（Markov Chain Monte Karlo，MCMC）。马尔科夫链定义本身比较简单，它假设某一时刻状态转移的概率只依赖于它的前一个状态。MCMC的原理是：从某个可取任意值的状态$x$出发，随着时间的推移，随即反复的更新状态$x$，最终$x$会成为一个从$p(x)$中抽出的（非常接近）比较一般的样本。在MCMC的马尔可夫链中包含两个部分：

• 随机状态$x$：表示某时刻的状态
• 转移分布$T(x^{\prime }|x)$：表示从$x$随即转移到$x^{\prime }$的概率

下面考虑并行运行多个马尔可夫链的情况，其中每一个均是采样自$q(x)$，使用$q^0$来初始化$x$。如果用向量描述$q(x)$有$q(\mathrm{x}=i)=v_i$，对于单一链的状态转移来说有$q^{(t+1)}\left(x^{\prime }\right)={\sum }_x{q}^{(t)}(x)T\left(x^{\prime }|x\right)$，进一步的将$T$看作矩阵$A:A_{i,j}=T\left({\mathrm{x}}^{\prime }=i|\mathrm{x}=j\right)$的话，有如下的推导$${\mathbf{v}}^{(t)}=A^t{v}^{(0)}={\left(\mathbf{V}\mathrm{diag}(\mathbf{\lambda }){\mathbf{V}}^{-1}\right)}^t{\mathbf{v}}^{(0)}=\mathbf{V}\mathrm{diag}(\mathbf{\lambda }{)}^t{\mathbf{V}}^{-1}{\mathbf{v}}^{(0)}$$

最终这个过程会收敛到均衡分布，得到$v^{\prime }=Av=v$，此时$q$将等于$p$。但是这样的方法也有很多的缺点：

• 无法预知何时到达均衡分布
• 到达均衡分布前磨合时间较长
• 采样两个互不相关的样本耗费时间较长

另外在确定$q(x)$是否为一个有效的分布时，常用的有两种方法：

• 从学习到的分布$p_{model}$中推导出$T$，如Gibbs采样
• 直接用参数描述$T$

因为目前还用不到，所以就不写啦~

P.S. GoodFellow的《Deep Learning》第17章第5小节关于不同的峰值之间的混合挑战部分很有意思，有兴趣的可以看一下.

17.5 The Challenge of Mixing between Separated Modes