本文探讨了词向量的表示方法，包括one-hot表示的局限性，以及通过词的分布特性进行词义推断的理论。重点介绍了Word2Vec模型，包括Skip-gram和CBOW两种算法，以及Hierarchical softmax和Negative sampling两种优化方法。
CS224n lecture 1 Introduction and Word Vectors
？如何来表示一个词的含义呢
如果我们遇到一个不认识的单词又想知道它的用法，最直接的一个方法就是查字典。根据字典中给出的关于单词的释义，我们就可以知道它的意思和具体的用法。一种理解单词意思的最普遍的语言方式是：
signifier <=> signified: 词的形式通常和词的意思具有很大的联系，这在存在大量象形字的汉字中尤其明显
signifier : n. （语言学）能指（语言的符号形式，区别于意义）；记号；表示者
signified : n. 所指（语言符号的意义）；意指
例如可以使用WordNet来进行词的查找，当我们输入 g o o d good good 时，它会给出相关的其他词
但是这种离散化的表示形式虽然可以很直接的被人使用，但是它也存在如下的缺点：
- 难以保留词之间微妙的差别：例如adept, expert, good, practiced, proficient, skillful意思在某种程度是相近的，但是它们通常距离很远
- 缺乏最新的词的信息，无法及时的更新
- 词之间的相似性、相异性很大程度上取决于人的主观判断
- 需要大量的人力
- 很难进行词的相似性度量（word similarity）
one-hot representation
因为绝大多数基于规则和统计的NLP工作都将单词视为原子符号（atomic symbols）如果我们想将它们表示在向量空间中，最简单的一种方式就是使用one-hot向量。首先为要处理的文本建立一个较大的词汇表，每个单词在词汇表中都有它的索引，例如单词Man，Woman，King，Queen，Apple，Orange分别出现在词汇表的第5391，9853，4914，7157，456，6257的位置；然后我们用和词汇表维度相同的one-hot向量表示每一个词，在向量对应的位置上取值为1，其余部分取值为0，记为 O i n d e x O_{index} Oindex。
但是one-hot 这样的表示方式存在如下的缺点，所以通常很难在实际应用中使用
- 每个词向量之间的内积为零，无法表示词之间的关系
- 词向量的维度和词汇表的大小相关，如果文本中不同的词特别多，词向量的维度将会变得很大
- 表示稀疏，浪费存储空间
Distributional similarity based representations
通常某一个词和某些其他的词总是共同出现，因此可以通过分析它周围的词的依赖来推断它的含义，这种方式成功广泛的应用在统计NLP模型中。
“You shall know a word by the company it keeps” (J. R. Firth 1957: 11)
Featurized representation
我们也可以使用特征表征的方法来对每个单词进行编码，即用不同的特征向量来表示不同的单词，特征向量中每一维都是对于单词某一个特征的描述，相关性的量化范围是 [ − 1 , 1 ] [-1,1] [−1,1]。例如上述的Man，Woman，King，Queen，Apple，Orange就可以使用Gender、Royal、Age等特征组成的特征向量进行表示
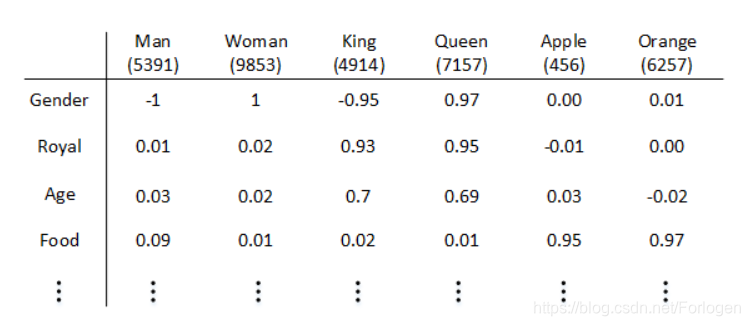
其中特征向量的长度取决于你设定的特征的数量，当然特征数量越多表示的信息越全面，但同时也会增加计算量。如果我们将长度设定为300的话，每一个单词都可以使用 300 × 1 300 \times 1 300×1的特征向量唯一的表示，可记为 e i n d e x e_{index} eindex。
通过比较不同单词特征向量之间的差异，我们就可以在一定程度上衡量两者的相似性，极大的提高了在有限词汇量下模型的泛化能力。这样的表示方式也称为 w o r d e m b e d d i n g word \ embedding word embedding ，本质上就是将高维稀疏的向量降维成稠密的低维向量，完成一种高维到低维的映射。
学习word embedding的相关方法有：
- Learning representations by back-propagating errors (Rumelhart et al., 1986)
- A neural probabilistic language model (Bengio et al., 2003)
- NLP (almost) from Scratch (Collobert & Weston, 2008)
- word2vec (Mikolov et al. 2013)
其中最著名的便是Tomas Mikolov等人提出的word2vec。
Mikolov T , Chen K , Corrado G , et al. Efficient Estimation of Word Representations in Vector Space[J]. Computer Science, 2013. arXiv:1301.3781v3
Mikolov T, Sutskever I, Kai C, et al. Distributed representations of words and phrases and their compositionality [J]. Advances in Neural Information Processing Systems, 2013, 26:3111-3119. arXiv"1310.4546v1
而通过神经网络来学习word embedding的基本思路为：对于给定中心词 w t w_{t} wt，预测它的上下文是计算后验概率 p ( c o n t e x t ∣ w t ) p(context|w_{t}) p(context∣wt) ，损失函数定义为 J = 1 − p ( w − t ∣ w t ) J=1-p(w_{-t}|w_{t}) J=1−p(w−t∣wt)，然后在大型语料库上进行训练来最小化损失函数，希望调整词向量到最佳。下面我们就来看一下word2vec是如何通过神经网络来得到一个好的词嵌入的。
在word2vec的提出论文中主要包括Skip-gram（SG）和Continuous Bag of Words（CBOW）两种算法模型，其中又包含了两种提升模型训练的方法Hierarchical softmax和Negative sampling。
Skip-gram（SG）
SG示意图
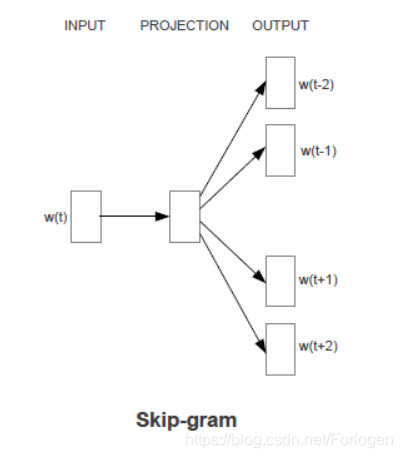
Skip-gram 模型思想是根据给定的中心词(center word)，并预测它的窗体大小范围内的上下文单词，训练目标是最大化概率分布。
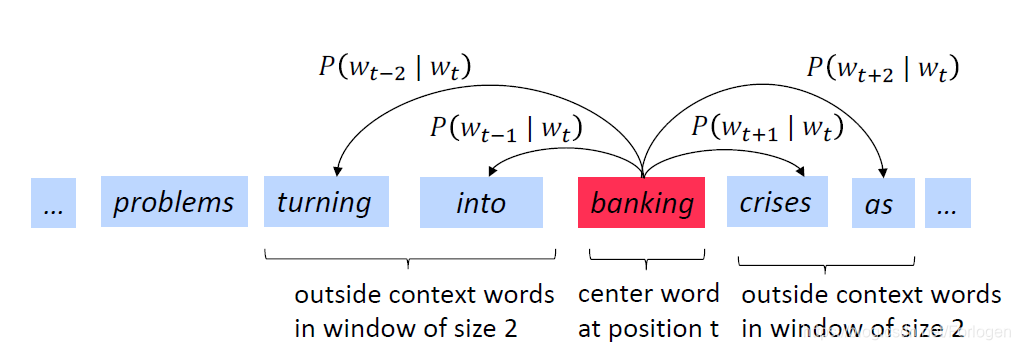
如上所示，当选择的中心词为
b
a
n
k
i
n
g
banking
banking，窗口大小为
m
m
m时，SG通过计算
p
(
w
t
−
m
∣
w
t
)
p(w_{t-m}|w_{t})
p(wt−m∣wt)和
p
(
w
t
+
m
∣
w
t
)
p(w_{t+m}|w_{t})
p(wt+m∣wt)来预测
w
t
w_{t}
wt的上下文单词。具体来说，当文本中的词汇表大小为
T
T
T时，对于每一个词
w
t
,
t
=
1
,
2
,
.
.
.
,
T
w_{t},t=1,2,...,T
wt,t=1,2,...,T来预测窗口大小为
m
m
m的上下文单词即最大化
w
i
w_{i}
wi的每一个上下文单词的预测概率
J
′
(
θ
)
=
∏
t
=
1
T
∏
−
m
≤
j
≤
m
T
p
(
w
t
+
j
∣
w
t
;
θ
)
J'(\theta)=\displaystyle \prod^{T}_{t=1}\displaystyle \prod^{T}_{-m\leq{j}\leq{m}}p(w_{t+j}|w_{t};\theta)
J′(θ)=t=1∏T−m≤j≤m∏Tp(wt+j∣wt;θ)
其中
θ
\theta
θ即模型需要优化的参数列表。通常需要使用极大似然估计来进行优化，因此最后使用的大多是负对数的形式
J
(
θ
)
=
−
1
T
∑
t
=
1
T
∑
m
≤
j
≤
m
l
o
g
p
(
w
t
+
j
∣
w
t
)
J(\theta)=-{\frac{1}{T}}\displaystyle \sum^{T}_{t=1}\displaystyle \sum_{m\leq{j}\leq{m}}log\, p(w_{t+j}|w_{t})
J(θ)=−T1t=1∑Tm≤j≤m∑logp(wt+j∣wt)
note: loss function = cost function = objective function
对于概率分布计算的损失项来说，同时选择使用的是交叉熵损失（cross-entropy loss）。
对于
p
(
w
t
+
j
∣
w
t
)
p(w_{t+j}|w_{t})
p(wt+j∣wt)的计算，如果用
o
o
o表示输出词向量对应词的索引，
c
c
c 表示中心词对应的词的索引，
v
c
v_{c}
vc表示中心词的词向量，
u
o
u_{o}
uo表示输出词的词向量，计算公式为：
p
(
o
∣
c
)
=
e
x
p
(
u
o
T
v
c
)
∑
w
=
1
V
e
x
p
(
u
w
T
v
c
)
p(o|c) = \displaystyle \frac{exp({u_{o}}^Tv_{c})}{\sum_{w=1}^V exp({u_{w}}^Tv_{c})}
p(o∣c)=∑w=1Vexp(uwTvc)exp(uoTvc)
其中
u
T
v
=
u
⋅
v
=
∑
i
=
1
n
u
i
v
i
u^Tv=u\cdot v = \displaystyle\sum_{i=1}^{n}u_{i}v_{i}
uTv=u⋅v=i=1∑nuivi表示
u
u
u和
v
v
v之间的点乘（dot-product），如果两个词越相似，它们对应词向量的点乘的结果就越大。为了输出
[
0
,
1
]
[0,1]
[0,1]之间的概率值，最后需要使用softmax函数
p
i
=
e
u
i
∑
j
e
u
j
p_{i}= \displaystyle \frac{e^{u_i}}{\sum_je^{u_j}}
pi=∑jeujeui。
一个Skip-gram的完成示例过程如下所示
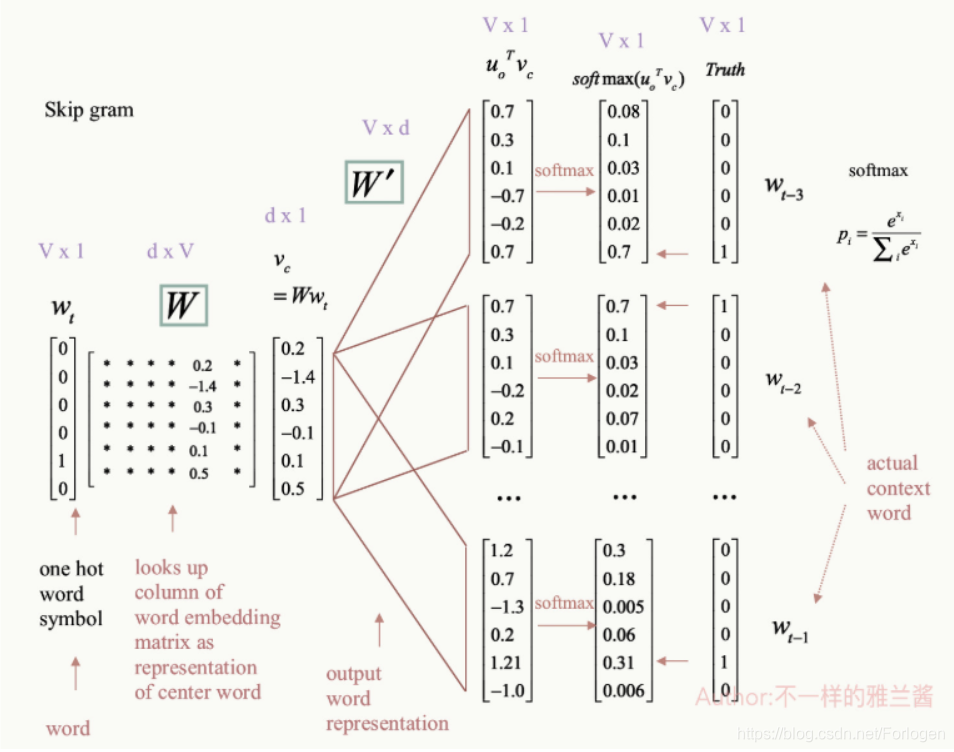
感谢雅兰同学的辛苦绘图~
首先以中心词 w t w_{t} wt 的one-hot表示作为输入，输入层到投影层之间有一个中心词的表示矩阵W，我们需要用向量乘以该矩阵从而选出矩阵中的对应列(column)即为中心词的表示形式。接下来，我们从投影层到输出层有第二个矩阵，存储着上下文单词的表示。这里会对中心词和上下文单词之间做点乘(dot product)，对于点乘之后的向量结果有正有负，我们会对其进行softmax处理，将其转化为一种概率分布。
在模型的训练中，我们实际要做的就是使用梯度下降最小化损失项来优化参数向量
θ
\theta
θ。
θ
=
[
v
aardvark
v
a
⋮
v
z
e
b
r
a
u
a
a
r
d
v
a
r
k
u
a
⋮
u
z
e
b
r
a
]
∈
R
2
d
V
\theta=\left[\begin{array}{c}{v_{\text {aardvark}}} \\ {v_{a}} \\ {\vdots} \\ {v_{z e b r a}} \\ {u_{a a r d v a r k}} \\ {u_{a}} \\ {\vdots} \\ {u_{z e b r a}}\end{array}\right] \in \mathbb{R}^{2 d V}
θ=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡vaardvarkva⋮vzebrauaardvarkua⋮uzebra⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤∈R2dV
要最小化的损失函数为
J
′
(
θ
)
=
∏
t
=
1
T
∏
−
m
≤
j
≤
m
T
p
(
w
t
+
j
∣
w
t
;
θ
)
J'(\theta)=\displaystyle \prod^{T}_{t=1}\displaystyle \prod^{T}_{-m\leq{j}\leq{m}}p(w_{t+j}|w_{t};\theta)
J′(θ)=t=1∏T−m≤j≤m∏Tp(wt+j∣wt;θ) ，训练的目标为
max
J
′
(
θ
)
=
∏
t
=
1
T
∏
−
m
≤
j
≤
m
T
p
(
w
t
+
j
∣
w
t
;
θ
)
\max J'(\theta)=\displaystyle \prod^{T}_{t=1}\displaystyle \prod^{T}_{-m\leq{j}\leq{m}}p(w_{t+j}|w_{t};\theta)
maxJ′(θ)=t=1∏T−m≤j≤m∏Tp(wt+j∣wt;θ)或是
min
J
′
(
θ
)
=
−
∏
t
=
1
T
∏
−
m
≤
j
≤
m
T
p
(
w
t
+
j
∣
w
t
;
θ
)
\min J'(\theta)= - \displaystyle \prod^{T}_{t=1}\displaystyle \prod^{T}_{-m\leq{j}\leq{m}}p(w_{t+j}|w_{t};\theta)
minJ′(θ)=−t=1∏T−m≤j≤m∏Tp(wt+j∣wt;θ)，具体梯度下降的过程为：
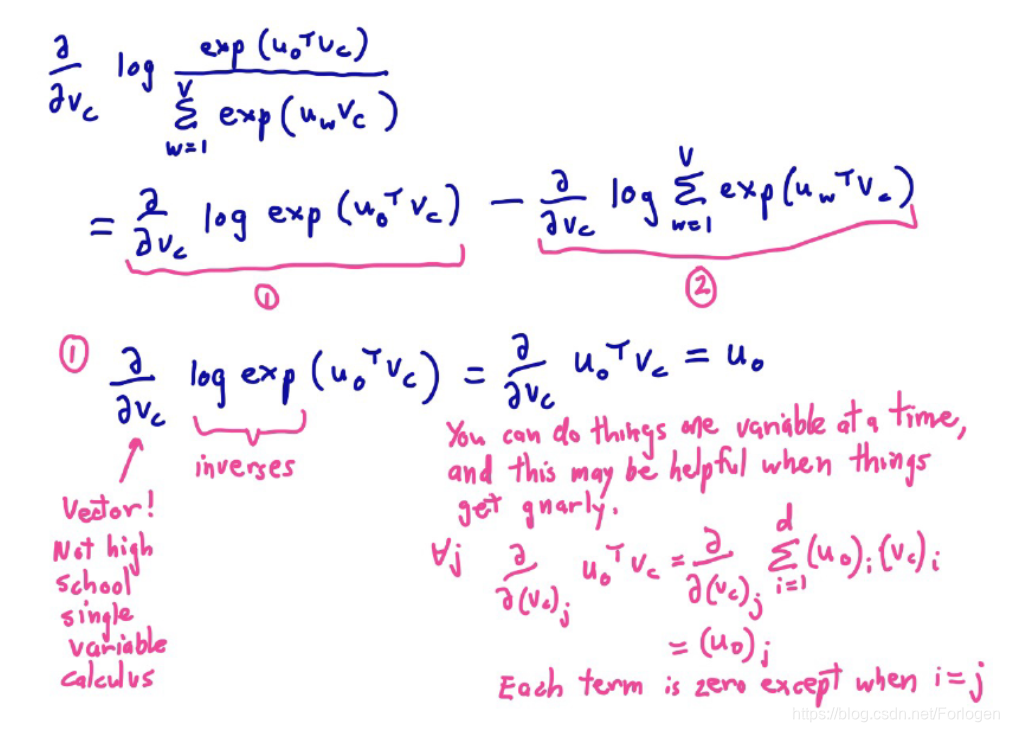
有关梯度下降的介绍可见：https://blog.youkuaiyun.com/Forlogen/article/details/88778770
参考
word2vec原理(一) CBOW与Skip-Gram模型基础
word2vec原理(二) 基于Hierarchical Softmax的模型
word2vec原理(三) 基于Negative Sampling的模型
一文详解 Word2vec 之 Skip-Gram 模型（结构篇）
一文详解 Word2vec 之 Skip-Gram 模型（训练篇）
一文详解 Word2vec 之 Skip-Gram 模型（实现篇）
word2vec原理推导与代码分析
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
