RobGAN

CVPR 2019 《Rob-GAN: Generator, Discriminator, and Adversarial Attacker》

github

本文作者创新性的将对抗学习（Adversarial learning）和生成对抗网络（Generative Adversarial Networks）组成一个新的模型，将生成器（Generator）、判别器（Discriminator）和对抗攻击者（Adversarial attacker）组合训练，提出了一种新的框架Rob-GAN。通过在传统的GAN中引入对抗学习中的Adversarial attacker，不仅可以加速GAN的训练，提高生成图像的质量，更重要的可以得到鲁棒性更好的判别器。

模型整体的结构可以看作是GAN和Adversarial attacker的一个组合形式。GAN部分继承自SNGAN，只有很小的改变，Adversarial attacker使用PD-attack来产生对抗样本，模型整体结构如下所示:

A. Madry, A. Makelov, L. Schmidt, D. Tsipras, and A. Vladu. Towards deep learning models resistant to adversarial attacks. arXiv preprint arXiv:1706.06083, 2017. 1
T. Miyato, T. Kataoka, M. Koyama, and Y. Yoshida. Spectral normalization for generative adversarial networks. In International Conference on Learning Representations, 2018

---

补充知识
对抗样本指的是一个经过微小调整就可以让机器学习算法输出错误结果的输入样本。在图像识别中，可以理解为原来被一个卷积神经网络（CNN）分类为一个类（比如“熊猫”）的图片，经过非常细微甚至人眼无法察觉的改动后，突然被误分成另一个类（比如“长臂猿”），如下所示

对于文中实验所选择PGD-attack来说，它的损失函数可以简单的总结为：$$\delta :=\underset{\Vert \delta \Vert \le {\delta }_{\max }}{\mathrm{argmax}}\ell (f(x+\delta ;w),y)$$
即表示了攻击者希望通过对输入的图像加上一些小的扰动，就可以使得分类器给出和原始标签完全不同的类判别结果。有攻击自然就有防御，对于防御者来说，它的损失函数如下所示：$$\underset{w}{\min }\underset{(x,y)\sim {\mathcal{P}}_{\text{ data }}}{E}\left[\underset{\Vert \delta \Vert \le {\delta }_{\text{ max }}}{\max }\ell (f(x+\delta ;w),y)\right]$$即判别器希望更好的把握数据的真实分布，提高本身的鲁棒性。

关于对抗学习的知识这里只做简单的介绍，等端午假期再做单独的总结

---

下面我们就来跟着作者的思路，欣赏一下Rob-GAN是如何被提出的。

根据模型的整体结构我们可以看出，生成器产生假样本希望骗过判别器，对抗攻击者对输入样本做一些小的扰动，同样也希望判别器做出错误的判断，而判别器则希望尽可能的判别出输入样本来自真实数据分布还是其他来源，因此判别器不仅需要判别样本是否真实，还需判断样本的类别。

那为什么它们三个可以很好的在一起工作，并最终也可以取得不错的效果呢？下面先来思考两个问题：

• 为什么GAN能通过对抗性训练提高判别器的鲁棒性?
• 为什么对抗攻击者可以提升GAN的训练?

---

The generalization gap of adversarial training— GAN aided adversarial training

对于现有的很多对抗防御的方法来说，它们可以在小的训练集上得到一鲁棒性较好的判别器，但是一旦在测试集上使用时，性能往往会有大幅的下降，并且这种现象在较大的数据集（如ImageNet）上更加显著。为什么会出现这么巨大泛化性能的差距呢？应该使用什么样的方法来解决呢？

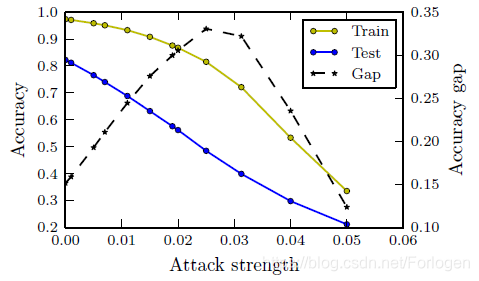
理论上来说，为了使模型的鲁棒性更好，我们希望在真实数据分布$P_{data}$下，局部的LLV（local Lipschitz value）值很小，而对于LLV的约束可以表示为一个复合损失最小化问题：$$\underset{w}{\min }\underset{(x,y)\sim {\mathcal{P}}_{\text{ data }}}{E}\left[\ell (f(x;w),y)+\lambda \cdot {\Vert \frac{\partial }{\partial x}\ell (f(x;w),y)\Vert }_2\right]$$

对Lipschitz 约束不熟悉的，可以看一下WGAN的提出论文《Towards Principled Methods for Training Generative Adversarial Networks》

但是在绝大多数情况下，我们是不知道数据的真实分布$P_{data}$的，故最终使用的是先验分布，如下所示：
$$\underset{w}{\min }\frac{1}{N_{\mathrm{t}\mathrm{r}}}\sum _{i=1}^{N_{\mathrm{t}\mathrm{r}}}\left[\ell \left(f\left(x_i;w\right),y_i\right)+\lambda \cdot {\Vert \frac{\partial }{\partial x_i}\ell \left(f\left(x_i;w\right),y_i\right)\Vert }_2\right]$$

如果我们拥有足够多的数据，以及假设集足够的大，理论上使用先验分布的模型得到的效果最终会逼近于采用真实数据分布的模型。
那么使用先验分布不会影响模型的效果，如果可以将对局部LLV值得约束泛化到测试集上，那么就可能会解决这种巨大泛化差距的问题。
为了验证这个猜想，作者分别对训练集和测试集的样本计算了Lipschitz值，如下所示：

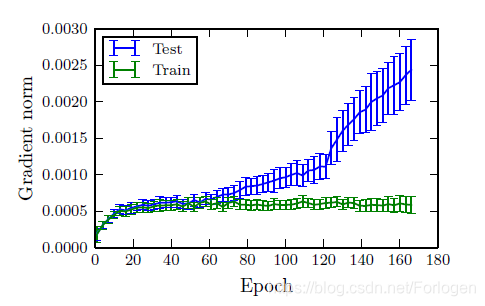
从中我们可以看出，在训练集和测试集上，随着迭代次数的增多，Lipschitz值上同样也存在巨大的差距，因此我们可以得出这样的结论：

在训练集上有效的约束LL值，模型的效果并不能泛化到测试集上！

如果不是采用上述的约束LLV值的方式，在有限的数据集上来逼近最优模型，而是直接从$P_{data}$中进行采样呢？而这不正是GAN的思想嘛？因此，一个很自然的想法就是：是否可以利用GAN学习$P_{data}$，然后对所学分布进行对抗性训练呢？如果可行的话，我们就可以使用GAN加对抗性训练的方式得到一个鲁棒性更好的判别器。因此损失函数可以看为对原始训练数据和合成的数据复合的形式，如下所示：
$$\begin{array}{l}{\min }_w{\mathcal{L}}_{\text{ real }}\left(w,{\delta }_{\max }\right)+\lambda \cdot {\mathcal{L}}_{\text{ fake }}\left(w,{\delta }_{\text{ max }}\right)\\ {\mathcal{L}}_{\text{ real }}\left(w,{\delta }_{\text{ max }}\right)\triangleq \frac{1}{N_{\text{ tr }}}{\sum }_{i=1}^{N_{\text{ tr }}}{\max }_{\Vert {\delta }_i\Vert \le {\delta }_{\text{ max }}}\ell \left(f\left(x_i+{\delta }_i;w\right);y_i\right)\\ {\mathcal{L}}_{\text{ fake }}\left(w,{\delta }_{\text{ max }}\right)\triangleq {\max }_{(x,y)\sim {\mathcal{P}}_{\text{ fake }}\Vert \delta \Vert \le {\delta }_{\text{ max }}}\ell (f(x+\delta ;w);y)\end{array}$$

然后同样使用随机梯度下降法进行优化，就可以达到理想的效果。

---

Accelerate GAN training by robust discriminator

设想一下，如果判别器的能力不强，或是鲁棒性不好的话，对抗样本就可以很容的骗过它，而且一旦生成器也采用和对抗样本类似的方式生成假样本，判别器不但无法判断出样本的真实类别，同时也无法判断出样本的真假，这样的话就永远无法抵达纳什均衡点，模型永远不会收敛。那么如果反过来想的话，如果判别器的鲁棒性足够好的话，它可以很容易的判别出样本的真假和对应的类别，那么它就可以给生成器提供更强的梯度信息，使得生成器生成的图像所满足的分布$P_G$更快的接近真实分布$P_{data}$，训练过程自然也就会变快。

而在稳定GAN训练过程的诸多技术中，虽然达到了稳定的效果，但同时也损害了模型的表达能力。我们希望的是能否采用一种较弱但是效果又好的正则化方法，实现两全其美的目的，即要求在图像的流形上有一个小的局部Lipschitz值，而不是一个严格的全局one-Lipschitz函数。而这可以通过对鉴别器进行对抗性训练很方便地完成，这样就可以将鉴别器的鲁棒性与生成器的学习效率联系起来。

如上图所示，如果对于图像的扰动$\delta$很小，那么它满足的分布仍然是很大程度上和假样本的分布重合，这样判别就可以大概率的进行正确的判别。假设将attacker也看做是一个生成器$G(z;w)$，如果$t$时刻判别器可以准确的判别出生成的"假样本"，那么下一时刻，attacker需要做什么来使得判别器无法正确判别生成的假样本，使得$D\left(G\left(z;w^{t+1}\right)\right)\approx 1$呢？通过对$D(x)$和$G(z;w)$连续性的Lipschitz连续性假设，我们可以得到一个下界，如下所示：
$$\begin{array}{l}1\approx D\left(G\left(z;w^{t+1}\right)\right)-D\left(G\left(z;w^t\right)\right)\\ \lesssim \Vert D^{\prime }\left(G\left(z;w^t\right)\right)\Vert \cdot \Vert G\left(z;w^{t+1}\right)-G\left(z;w^t\right)\Vert \\ \lesssim \Vert D^{\prime }\left(G\left(z;w^t\right)\right)\Vert \cdot \Vert \frac{\partial }{\partial w}G\left(z;w^t\right)\Vert \cdot \Vert w^{t+1}-w^t\Vert \\ \le L_D{L}_G\Vert w^{t+1}-w^t\Vert \end{array}$$

进一步可以写做$\Vert w^{t+1}-w^t\Vert \propto \frac{1}{L_D{L}_G}$，其中$L_D$和$L_G$是常量，可以看出生成器参数的更新反比于左式的后一部分，也就是说，如果判别器的鲁棒性很差，对应的$L_D$就会很大，因为它处于分母的位置，这是参数的变化量就相对很小，即收敛的速度就很慢，这就证明了判别器的鲁棒性对于生成器更新的速度起着至关重要的影响，同时也就显示了，在GAN中引入对抗学习的Attacker来增强判别器的鲁棒性对于加快收敛有着理论上的意义，而且作者也是实验中证明了它的可行性。

---

Rob-GAN

根据上面的分析，我们知道GAN和对抗学习的结合是可行的，将它们结合起来就是Rob-GAN。Rob-GAN模型的架构并不复杂，判别器的网络结构和损失函数直接使用ACGAN

A. Odena, C. Olah, and J. Shlens. Conditional image synthesis with auxiliary classifier gans. In International Conference on Machine Learning

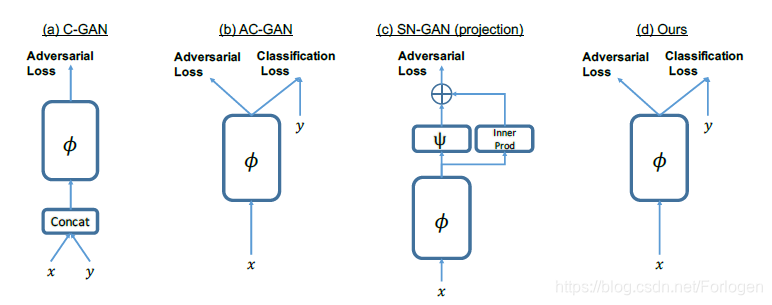
对应的损失函数如下所示：
$$\begin{array}{rl}{\mathcal{L}}_S& =\mathbb{E}\left[\log \mathbb{P}\left(S=\mathrm{real}|X_{\text{ real }}\right)\right]+\mathbb{E}\left[\log \mathbb{P}\left(S=\text{ fake }|X_{\text{ fake }}\right)\right]\\ {\mathcal{L}}_C& =\mathbb{E}\left[\log \mathbb{P}\left(C=c|X_{\text{ real }}\right)\right]+\mathbb{E}\left[\log \mathbb{P}\left(C=c|X_{\text{ fake }}\right)\right]\end{array}$$

对于Rob-GAN的判别器来说，它不仅要判别输入样本的真假，还要判别它所属的类别。但是如果生成的图像很糟糕的话，判别仍要花大量的精力去给出一个类别结果，而且此时分类的梯度信息对于判别器的更新并无帮助，因此将${\mathcal{L}}_c$分成如下的两部分：
$$\begin{array}{c}{\mathcal{L}}_{C_1}=\mathbb{E}\left[\log \mathbb{P}\left(C=c|X_{\text{ real }}\right)\right]\\ {\mathcal{L}}_{C_2}=\mathbb{E}\left[\log \mathbb{P}\left(C=c|X_{\text{ fake }}\right)\right]\end{array}$$

判别器最大化${\mathcal{L}}_S+{\mathcal{L}}_{C_1}$，生成器最大化${\mathcal{L}}_{C_2}-{\mathcal{L}}_S$，这样新的目标函数保证了识别器只专注于对真实图像的分类和真伪图像的识别，而且分类器分支不会受到虚假图像的干扰。

对于生成器来说，如果样本很少的话，它只覆盖了数据流形的很小一部分，那么在测试时就会出现上述的第一个问题。传统的数据增强技术虽然能增加样本的数量，但是仍不能满足要求。而Rob-GAN使用生成器生成样本来不断的增加样本的数量，从而为对抗训练提供一个连续支持的概率密度函数

our system has unlimited samples from generator to provide a continuously supported probability density function for the adversarial training

如果可以到达纳什均衡点，即${\mathcal{P}}_{\text{ fake }}(z)\stackrel{\text{ dist }}{=}{\mathcal{P}}_{\text{ real }}$，此时分类器分支就相当于在真实样本集上训练，也就避免了上述的问题。

另外，如果我们单纯的想让判别器进行多分类任务的话，就需要对其进行微调，将假样本和真实样本结合起来，然后如下的损失函数这样便可以大幅的提高分类的准确性

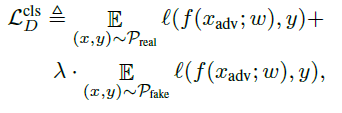
这样的过程称为fine-tuning

---

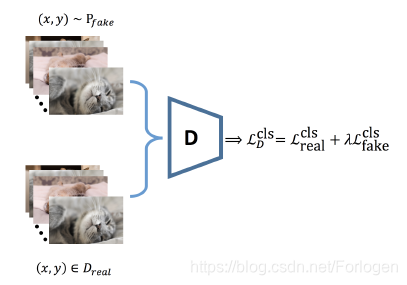
Experiments

数据集：CIFAR10和只取143类的ImageNet

从下图可以看出，fine-tuning和augmentation对于模型效果的提升是显著的

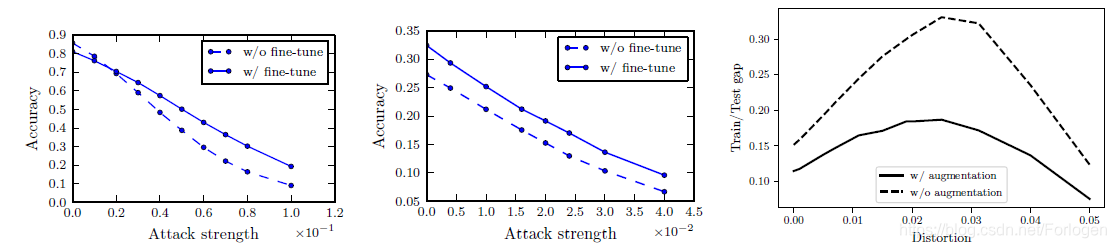
下图显示了在不同大小的扰动下，模型在分类准确率上的表现

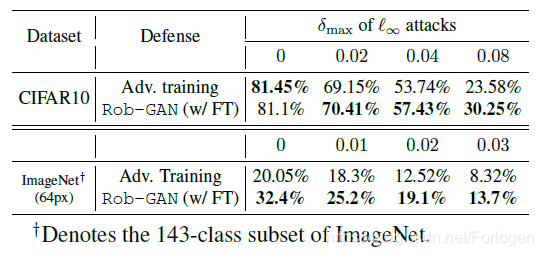
下图左边为Rob-GAN生成的图像，右图是ACGAN生成的图像，从中我们可以看出Rob-GAN的图像的质量要由于ACGAN

下图显示了Rob-GAN的三个优势：

• 与SN-GAN相比，我们的模型(new loss + adversarial)有效地学习了一个高质量的生成器
• 当将新的损失与原来的损失进行比较时，我们看到新的损失表现得更好
• 利用新的损失，对抗性训练算法具有很好的加速效果
  

---

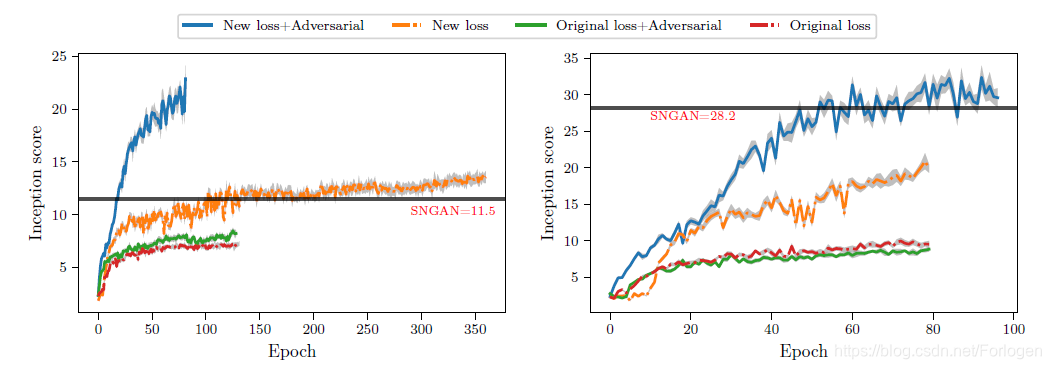
总结

整篇文章看下来给人一种身心畅快的感觉，没有繁杂的模型堆砌，没有复杂的数学公式，而是对于GAN本身所存在的一些问题做了理论解释，以及实验证明了为何引入Adversarial learning后可以在一定程度上达到作者所说的效果。