如何更直观的理解GANs？

ICLR 2019 《GAN DISSECTION: VISUALIZING AND UNDERSTANDING GENERATIVE ADVERSARIAL NETWORKS》

github

Demo

project page

从2014年GoodFellow发表了《Generative Adversarial Nets》后，生成对抗网络（GAN）逐渐称为深度学习领域一个极其热门的方向，很多的人前赴后继的投入到了GAN的研究中。有的人针对于最初提出的标准GAN中所存在的一些问题做出了改进，提出了一系列GAN的变种，如WGAN、LSGAN、EBGAN……也有的人推进了GAN在其他领域的应用，如进行风格迁移的CycleGAN、DualGAN、XGAN、StarGAN、CoGAN……，应用于生成超分辨率图像的BigGAN、LAPGAN、PGGAN、SRGAN、StackGAN、StyleGAN……，进行特征提取的VAEGAN、InfoGAN、BiGAN……，除了针对于GAN本身的改进，当然还有很多的研究者将其和NLP、RL等领域的问题相结合，也取得了不错的效果。

虽然在2014年后，GAN的发展有了显著的进步，但是仍然缺乏理解GAN工作机制的方法。虽然GAN可以生成高质量的图像，但是无从知道生成的结果在它的内部是如何表示的；不同的GAN的改进变种在论文的实验部分都显示了比将其作为实验基准的其他GANs效果好，但是无法从内部的结构来理解为何会造成效果的显著性提升（这里不着重考虑算力和数据量的差异）。因此，如何合理的可视化和理解GANs成为了一个急需解决的问题。

本文作者从其他网络模型（如CNN、RNN等）的可视化方法中得到启发，提出了一个新的分析框架，它可以实现从单元（unit）、实体对象（object）和场景（scene）三个不同的层级上，从低到高的理解GAN内部的工作机制。它的整个实现机制主要分为两步：

• 剖析（Dessection）：利用分割模型定义一组和实体对象相关联的可解释性单元
• 干涉（Intervention）：通过控制这些可解释性单元对实体输出效果的差异的影响，进而理解它们之间的因果牵连。

最后作者通过实验显示了如何使用该框架实现在不同层次、不同模型、不同数据集上内部表示的对比；如使用它来分析GANs生成结果质量不高的原因，进而通过某些方法来帮助GANs生成更好的结果；如何使用它来分析和某一具体相关联的多个单元之间的重要性差异；如何使用它来理解不同的实体之间的上下文关系。总的来说，作者希望该框架可以帮助研究者和实践人员更好的理解自己的GANs。

本文的重要性不仅在于针对生成对抗网络这个领域所作出的开创性工作，它还有助于理解其他生成模型的工作机理，从而更好的理解生成结果的产生过程。

---

下面我们就来跟着作者的思想欣赏一下他们所提出的这个方法，在此之前，先对下面将要用的符号做一些规定：

• $z$ ：$\mathbf{z}\in {\mathbb{R}}^{|z|}$ ，表示采样自某个低维分布的噪声向量
• $G$：$G:z\to x$，表示生成器
• $x$：$\mathbf{x}\in {\mathbb{R}}^{H\times W\times 3}$表示生成样本，其中$H\times W$表示样本的尺寸，$3$表示彩色图像的三通道
• $r$：表示$G$中间层特征的表示张量
• $c$：表示输出实体的类别
• $\mathrm{U}$：表示每个通道的特征图，包含了和某一输出实体相关联的单元的集合，$\overline{\mathrm{U}}$表示无关联的单元集合
• $\mathrm{u}$ ：表示某一单元
• $\mathrm{P}$：表示$r$中的某一位置
• $\mathbb{U}、\mathbb{P}$：表示$r$中单元$u$和特征图的全集
• $\uparrow$：表示上采样
• $S_c(x)$：表示生成样本根据类$c$的语义分割的部分
• $r_{\mathrm{u},\mathrm{p}}$：表示关于某一实体类$c$ 的语义信息
• $t_{\mathrm{u},\mathrm{c}}$：关于$c$ 的某个单元$u$进行二值化的阈值

根据生成器的原理，有
$$r=h(\mathbf{z})\text{ and }\mathbf{x}=f(\mathbf{r})=f(h(\mathbf{z}))=G(\mathbf{z})$$
同时为了更好的理解$r$的哪些位置$\mathrm{P}$的的单元$\mathrm{U}$是和实体类型$c$相关的，我们将$r$分解为两部分：
$${\mathbf{r}}_{\mathbb{U},\mathrm{P}}=\left({\mathrm{r}}_{\mathrm{U},\mathrm{P}},{\mathrm{r}}_{\overline{\mathrm{U}},\mathrm{P}}\right)$$

---

Dissection

这是作者所提出的方法的第一步，总体思想是通过衡量实体类$c$和对应的$r$中的每个独立单元$u$ 的一致性来确定关于$c$的显示表达单元。

下面是这一步的图示化过程：

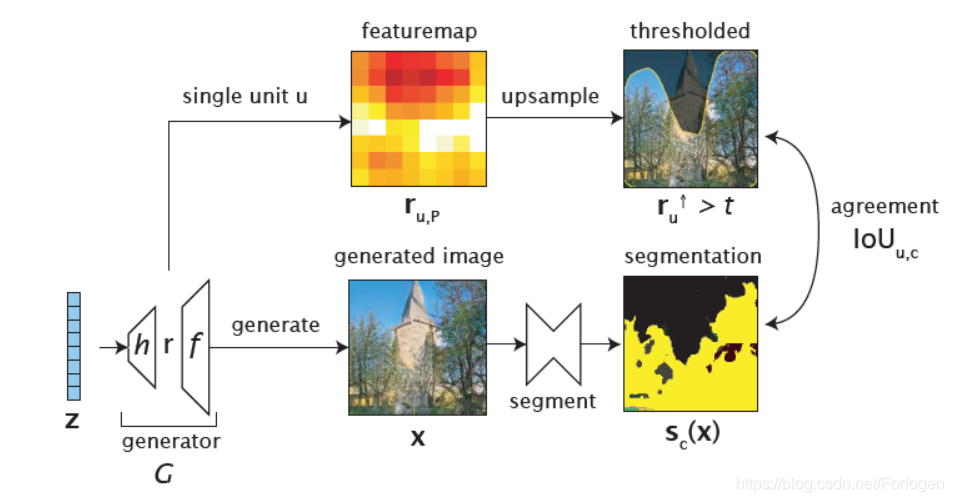
• 首先按照GAN正常的运行过程生成样本$X$ ，然后根据关注的语义利用语义分割模型得到分割后的结果$s_c(X)$

• 然后将$G$中间层的表征向量$r$ 的每个单元$u$ 所代表的特征图$r_{\mathrm{u},\mathrm{p}}$拿出，进行上采样并根据固定的标准$t_{\mathrm{u},\mathrm{c}}$进行二值化

  upsampling:Justbilinear interpolation. Which threshold? It’s possible to do the analysis by just choosing a naïve fixed threshold such as the top 1% level for the unit, but the paper makes a slightly different choice that maximizes relative mutual information between the feature and the segmentation label being matched.)

• 最后使用IOU来评估$u$上采样、二值化得到的结果和$S_c(x)$之间的一致性

  Using it to quantify how well the network is at solving each segmentation problem.

$${\mathrm{IOU}}_{u,c}\equiv \frac{{\mathbb{E}}_{\mathbf{z}}\left|\left({\mathrm{r}}_{u,\mathrm{P}}^{\uparrow }>t_{u,c}\right)\wedge {\mathrm{s}}_c(\mathrm{x})\right|}{{\mathbb{E}}_{\mathrm{z}}\left|\left({\mathrm{r}}_{u,\mathrm{p}}^{\uparrow }>t_{u,c}\right)\vee {\mathrm{s}}_c(\mathrm{x})\right|}$$

其中
$$t_{u,c}=\arg \underset{t}{\max }\frac{\mathrm{I}\left({\mathrm{r}}_{u,\mathrm{P}}^{\uparrow }>t;{\mathbf{s}}_c(\mathrm{x})\right)}{\mathrm{H}\left({\mathrm{r}}_{u,\mathrm{p}}^{\uparrow }>t,{\mathrm{s}}_c(\mathrm{x})\right)}$$
$t_{\mathrm{u},\mathrm{c}}$取信息质量率（information quality ratio）的最大值，它是从提前选择好的单独的验证集中计算得来的，与当前训练的数据无关。

通过上述过程我们就得到了和实体类$c$相关联的单元$u$ ，通常这些的单元会有多个，为了显示相对的重要性，需要将其进行按照IOU值的大小进行排序，顺序越靠前的自然和$c$ 的关联性越大。

但是在得到了一组相关的单元后，我们想知道哪些对于最后的输出样本是起到至关重要的作用呢？相关的不同的单元的组合又是如何影响最后的输出的？

---

Intervention

为了进一步回答上面的遗留问题，就需要进行第二个步骤：intervention。当找到了和具体的实体类别$c$相关联的某些单元时，通过强制的控制某些单元的“开和关”来研究它们和$c$之间的因果关系。

因此，按照前面的设置，当我们确定关闭某些单元时，就令$r_{U,P}=0$；当打开某些单元时，就令$r_{U,P}=k$，$k$这里是一个常数。然后重新分解$r$得到：
$$\begin{gathered} Originalimage:x=G(z)\equiv f(r)\equiv f(r_{\mathrm{U},\mathrm{P}},r_{\overline{\mathrm{U},\mathrm{P}}}) \\ Imagewith\mathrm{U}ablatedatpixels\mathrm{P}:X_a=f(0,r_{\overline{\mathrm{U},\mathrm{P}}}) \\ Imagewith\mathrm{U}insertedatpixels\mathrm{P}:X_i=f(k,r_{\overline{\mathrm{U},\mathrm{P}}}) \end{gathered}$$
其中$r_{\overline{\mathrm{U},\mathrm{P}}}$表示和$r$无关的部分。

然后，这里使用了通过比较$x_i$和$x_a$ 中树是否存在以及对所有位置和图像的平均效果来量化评估，即使用the average causal effect (ACE) ：
$${\delta }_{\mathrm{U}\to c}\equiv {\mathbb{E}}_{\mathbf{z},\mathrm{P}}\left[{\mathbf{s}}_c\left({\mathrm{x}}_i\right)\right]-{\mathbb{E}}_{\mathbf{z},\mathrm{P}}\left[{\mathbf{s}}_c\left({\mathrm{x}}_a\right)\right]$$
因为相关联的单元不止一个，因此需要确定的是一组可以使得${\delta }_{\mathrm{U}\to c}$值最大的单元集合$\mathrm{U}$。然而，接下来又会遇到一个新问题：我们相关探究相关的不同的单元的组合是如何影响最后的输出，但是简单的穷举搜索所有的单元组合是不太现实的。所以作者这里引入了一个优化的连续干扰项$\mathbf{\alpha }\in [0,1{]}^d$，，其中${\alpha }_{\mathrm{U}}$的每一维表示了对于$u$的干涉程度。按照下面的设置，来求${\delta }_{\mathrm{U}\to c}$的最大值：
$$\begin{gathered} Imagewithpartialablationatpixels\mathrm{P}:{\mathbf{x}}_a^{\prime }=f\left((1-\mathbf{\alpha })\odot {\mathbf{r}}_{\mathbb{U},\mathbf{P}},{\mathbf{r}}_{\mathbb{U},\overline{\mathbf{P}}}\right) \\ Imagewithpartialinsertionatpixels\mathrm{P}:{\mathbf{x}}_i^{\prime }=f\left(\mathbf{\alpha }\odot \mathbf{k}+(1-\mathbf{\alpha })\odot {\mathbf{r}}_{\mathbb{U},\mathbf{P}},{\mathbf{r}}_{\mathbf{U},\overline{\mathbf{p}}}\right) \\ Objective:{\delta }_{\mathbf{\alpha }\to c}={\mathbb{E}}_{\mathbf{z},\mathbf{P}}\left[{\mathbf{s}}_c\left({\mathbf{x}}_i^{\prime }\right)\right]-{\mathbb{E}}_{\mathbf{z},\mathbf{P}}\left[{\mathbf{s}}_c\left({\mathbf{x}}_a^{\prime }\right)\right] \end{gathered}$$
使用$L_2$正则化来优化$\alpha$ :
$${\mathbf{\alpha }}^{\ast }=\arg \underset{\mathbf{\alpha }}{\min }\left(-{\delta }_{\mathbf{\alpha }\to c}+\lambda \Vert \mathbf{\alpha }{\Vert }_2\right)$$
然后使用SGD来寻找结果，最后按照${\alpha }^{\ast }$对所有单元的组合进行排序，找出因果关系最大的单元集。

图示化过程如下所示

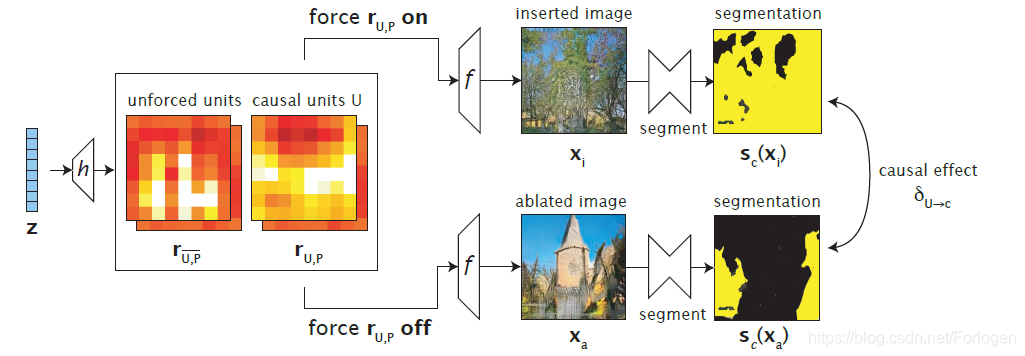
例如下图所示的实验结果，但我们去除的单元组合越多，树的数量越少，对应的右图中关于树的像素数量就越少，但留下的建筑的面积越大。

---

实验

作者在实验部分利用上面阐述的步骤研究了七个方面的问题。

1. 研究和实体类相关联的单元所表示的特征是否和人所关注的特征一致

   
   

   如上图所示，我们可以看出：在关于餐厅（dining room）的图像中，有大量的单元和桌子（table）相关联；而在关于客厅（living room）的图像中，相关联单元最多的是沙发（sofa），这样的结果也符合人类的判断准则。

2. 研究在表示某一实体时，不同相关的单元的可解释性

   
   

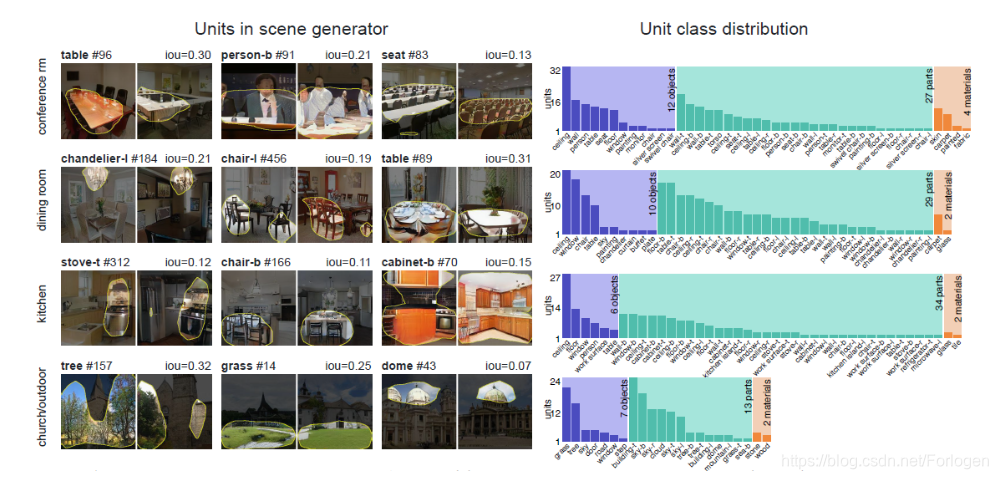
   如上图所示，利用语义分割模型得到的结果中，GAN所关注的是天花板、人、桌子、座位等；关于厨房的图像中，GAN关注的是天花板、窗户、椅子、桌子等……从中我们可以看出，GAN所重点关注的单元的组合和人的关注点是一致的。

3. 研究网络的不同层次的单元和输出实体之间的关联性

   
   

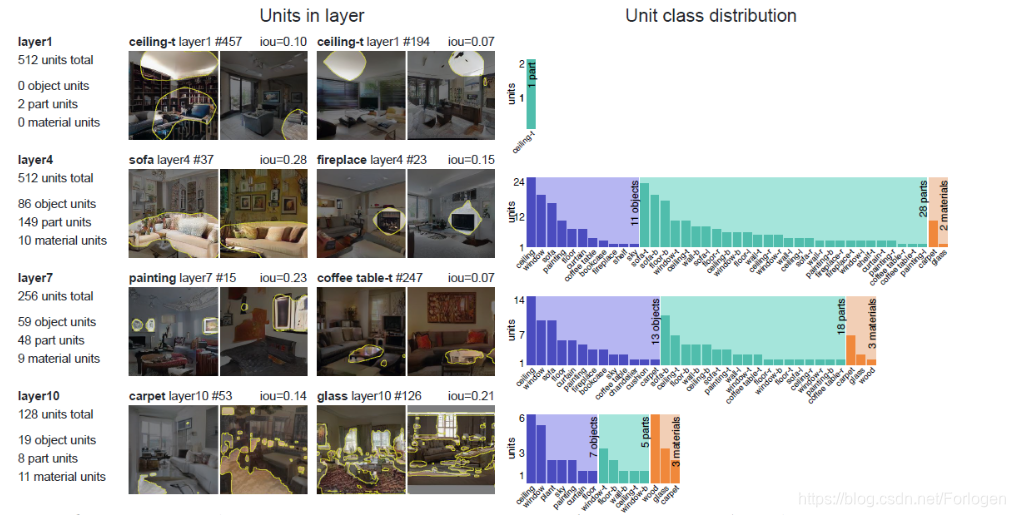
   如上图所示，当网络越深时，它所包含的单元所表达的语义信息和输出结果之间的关联越大，特别的在10层以上的单元主要是匹配局部的像素模式，如材质、颜色等。

4. 研究不同的模型的单元的可解释性

   
   

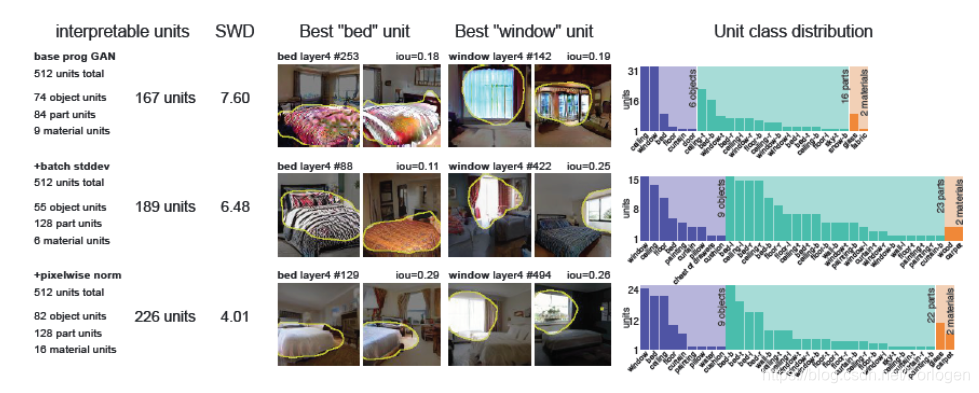
   如上图所示，随着模型质量的提高，可解释单元的数量也会增加。添加minibatch stddev statistics和pixelwise normalization对于效果都有很大的影响。

5. 研究为什么有时GAN会产生不好的生成样本，以及如何改进其效果？

   
   

   从图中可以看出，在图像质量不高的图像中，会有很多的artifact-causing units造成的伪影，当我们将其去掉后发现，生成的样本的质量有了显著的提高，并且超过了其他新的GAN的变体。

6. 研究不同的单元对于生成图像的相对重要性

   
   

   通过实验发现，在和某一实体相关联的诸多单元中，有些一处后只是会影响图像的质量，有些则根本无法移除。例如，我们可以移除会议室的窗户，但无法移除会议室的桌子、椅子。

7. 研究插入的单元和原有单元之间的上下文关系

   
   

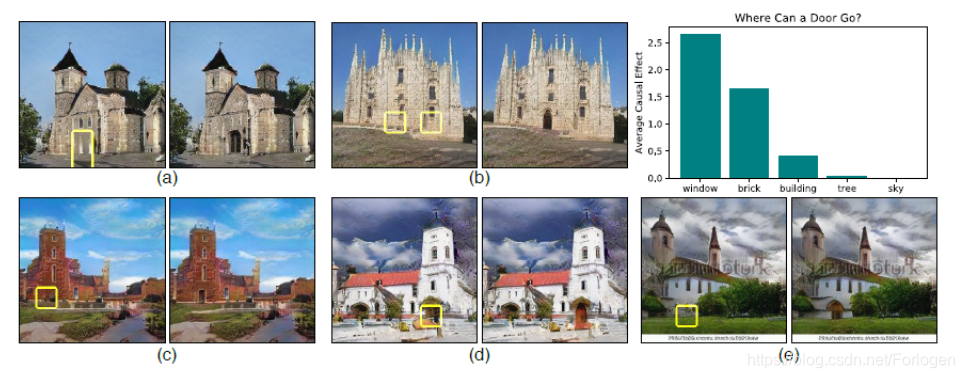
   在图中的不同位置添加门时发现，在大多数位置不能添加门。可以添加门的位置用黄色框突出显示。右上条形图显示了门单元插入的平均因果效应，取决于干预位置的背景对象类。我们发现，GAN允许在建筑物中添加门，特别是在有窗户或砖块的合理位置。相反，在天空或树上触发一扇门是不可能的。Intervention为我们提供了一种方法来加强对GAN如何加强对象之间关系的洞察。例如，即使我们试图在第4层中添加一个门，如果对象不适合上下文，那么稍后可以否决该选择。