LAPGAN

《Deep Generative Image Models using a Laplacian Pyramid of Adversarial Networks》

github

本文关注的是如何生成较高分辨率的图像这个传统的GAN无法解决的问题。相关的GAN的变体也有很多，像BigGAN、StackGAN、PGGAN、SRGAN等，而本文作者提出的是一种在拉普拉斯金字塔框架下使用级联卷积网络，从粗略到精细逐步生成高质量的自然图像的GAN的变体，称为LAPGAN。在金字塔的每一层都是使用GAN的方法训练单独的生成卷积网络模型，经过实验证明了LAPGAN的效果优于在它之前的其他相关的方法。

LAPGAN的关键之处在于它放弃了全局保真度的概念，即它不是专注于一次生成一张清晰的图像，而是专注于每一步的结果，让每次的生成结果都合理，逐步的生成清晰的结果。此外使用金字塔这样的结构，使得模型难以简单的记住训练实例来达到较好的效果。

整个LAPGAN的架构可以简单的看成是CGAN和拉普拉斯金字塔的一种结合，金字塔的每一层都是学习与相邻层之间的残差，也就是说，高分辨率图像的生成是以低分辨率图像作为条件去生成残差，然后低分辨率图上采样再跟残差求和得到高分辨率图，这种低分辨率图向高分辨率图生成的过程其实就是一个CGAN，通过不断堆叠 CGAN 得到我们想要的分辨率。

---

拉普拉斯金字塔

有关拉普拉斯金字塔和高斯金字塔的基本理解可参考：

https://zhuanlan.zhihu.com/p/32815143

简单的可以理解为：

• 高斯金字塔用于图像的下采样，相当于减小图像的尺寸，顺序是从底层到顶层
• 拉普拉斯金字塔用于图像的上采样，相当于扩大图像的尺寸，顺序是从顶层到底层，它需要配合高斯金字塔一起使用

下面看一下文章中对于拉普拉斯金字塔的介绍。它是线性可逆的图像表示，由一组带通图像组成，在空间上相隔一个八度，另加上低频残差。其中

• $d(.)$：下采样，它可以模糊和抽取$j\times j$的图像$I$，生成$\frac{j}{2}\times \frac{j}{2}$的新图像$d(I)$
• $u(.)$：上采样，它平滑和扩展图像为原图像$I$的两倍，即$u(I)$表示$2j\times 2j$的新图像

但是要使用拉普拉斯金字塔，首先要建立一个高斯金字塔$\mathcal{G}(I)=\left[I_0,I_1,\dots ,I_K\right]$，其中 $I_0=I$，$I_K$是重复应用$d(.)$到图像 $I$上的运算结果。例如，$I_2=d(d(I))$，$k$是所选择的的金字塔的级别数。拉普拉斯金字塔$\mathcal{L}(I)$的每个级别$k$处的参数$h_k$通过取高斯金字塔中的相邻级别之间的差异来构造，用 $u(.)$对较小的级别进行上采样，使得它们在大小上是兼容的：
$$h_k={\mathcal{L}}_k(I)={\mathcal{G}}_k(I)-u\left({\mathcal{G}}_{k+1}(I)\right)=I_k-u\left(I_{k+1}\right)$$
直观地说，每个级别捕获以特定比例呈现的图像结构。最后的拉普拉斯金字塔 $h_k$不是差异图像，而是等于最终高斯金字塔层级之间的低频残差，即 $h_k=I_k$。从拉普拉斯金字塔系数 $[h_1,...,h_k]$重建图像的方式是由后向前的进行如下迭代：
$$I_k=u\left(I_{k+1}\right)+h_k$$
以$I_k=h_k$开始，重建图像为$I=I_0$。换言之，从最粗糙的级别开始进行重复上采样，并将差异图像$h$ 添加到下一个更精细的级别，直到能够重建全分辨率的原始图像

---

LAPGAN

我们可以从样本生成的过程理解LAPGAN，如下所示

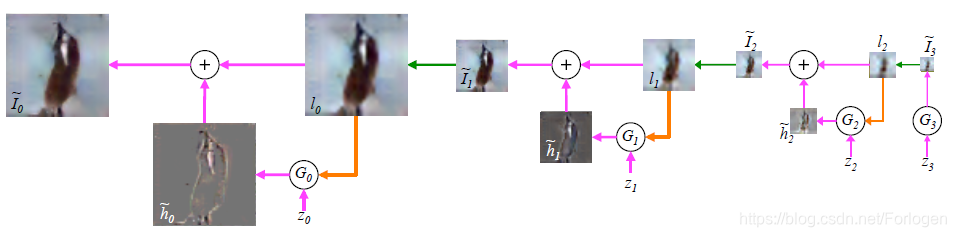
拉普拉斯金字塔的每一层都是由GANs组成，在顶层的生成器的输入只有噪声 $z$，而后像素更高的图像被用来训练CGAN，输入不光有噪声，还有同级的高斯金字塔的图像经过上采样得到的图像。每一层的GANs都用来捕获图像系数 $h_k$的分布，这个过程类似于上面 $I_k=u\left(I_{k+1}\right)+h_k$，只不过生成模型被用来生成 $h_k$:
$${\tilde{I}}_k=u\left({\tilde{I}}_{k+1}\right)+{\tilde{h}}_k=u\left({\tilde{I}}_{k+1}\right)+G_k\left(z_k,u\left({\tilde{I}}_{k+1}\right)\right)$$
例如， $\widetilde{I_2}$ 经过上采样得到 $l_1$ ，和随机噪声 $z_1$一起输入到 $G_1$中生成 $\widetilde{h_1}$，然后 $\widetilde{h_1}$和 $l_1$相加得到 $\widetilde{I_1}$ ，整个过程可以表示为 $\widetilde{I_1}=u(\widetilde{I_2})+G_1(z_1,u({\tilde{I}}_2))$。

其中每一层的生成模型$G_k$ 均使用CGAN的方法进行训练，$G_k$是粗尺度图像，输入为$\widetilde{I_k}$和$z_k$，而$D_k$将$\widetilde{h_k}$或$h_k$与低通图像$l_k$一起作为输入，并预测图像是真实样本还是生成样本。在金字塔的最后一层，低频残差足够小，可以用标准GAN直接建模$\widetilde{h_K}=G_K(z_K)$，$D_K$也只有$\widetilde{h_k}$或$h_k$作为输入，整个过程如下所示

---

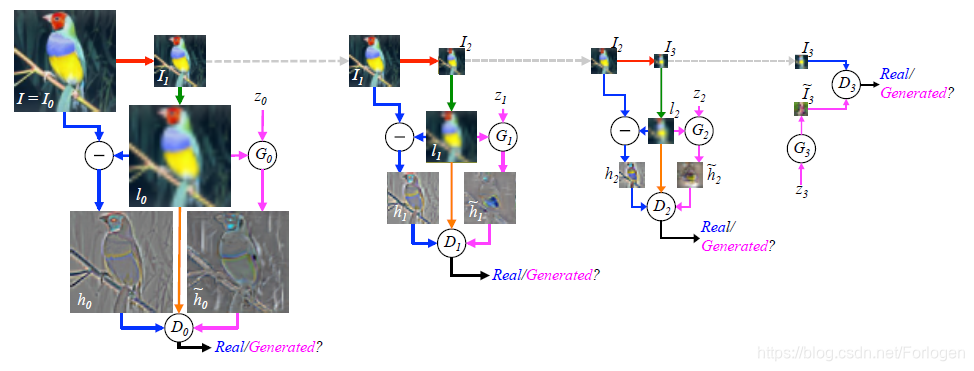
实验

作者在CIFAR10、STL、LSUN三个数据集上分别做了三中实验，验证LAPGAN的效果。

对数似然的估计

作者使用Gaussian Parzen窗口估计器来计算对数似然，从下图中可以看出，本文的方法的效果比GAN略微增加。LAPGAN模型的多尺度结构可以改进基础估算技术。这种新方法计算拉普拉斯金字塔每个尺度的概率，并将它们组合起来以得出整体图像的概率。

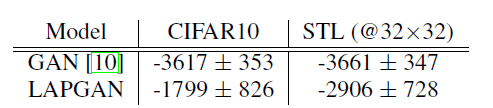
模型生成的样本

在CIFAR10，STL和LSUN数据集上训练的模型的生成样本依次如下所示

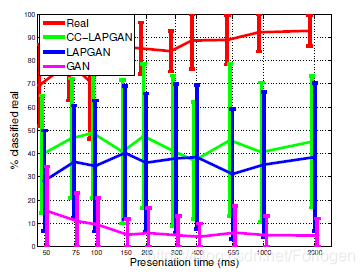
人类对样本的评价

为了获得样品质量的定量测量，作者邀请了15名志愿者参与实验，看看他们是否可以将样本与真实图像区分开来。结果显示LAPGAN模型产生的样本比标准GAN 更真实。

---

总结

作者提出了一种概念上简单的生成模型，能够生成高质量的样本图像，其质量优于其他深度生成建模方法。虽然它们表现出合理的多样性，但本文中无法确定它们是否涵盖了完整的数据分布。因此，本文的模型可能会在自然图像上为流形的某些部分分配低概率。量化这一点很困难，但可能通过人类主观的实验来完成。本工作的一个关键点是放弃任何“全局”保真度的概念，而是将其打破成合理的连续改进。注意到许多其他信号模型具有多尺度结构，可以从类似的方法中受益。