学习生成对抗网络,第一件事就是看这篇神作《Generative Adversarial Nets》,下面对这篇论文做一个学习的总结,主要关注于文中介绍生成对抗网络的部分,其余内容详见论文,它对于我们理解生成对抗网络不会有太大的影响。

总览
看一篇论文最重要的自然是先看摘要部分,下面我们看一下它对本文的主要内容是如何介绍的。
在本文中作者提出了一种新的框架,通过对抗的过程来评估生成模型,在这个过程中同时训练以下两个模型:
- 生成器(generative model,G):捕捉样本的分布规律
- 判别器(discriminative model ,D):判断输入的样本事来自真实的训练数据还是生成器G
G 的训练过程是让D犯错的概率最大化,作者提出的这个新的框架相当于一个极小化极大的双方博弈游戏的过程。在任意的G和D的空间中存在唯一的解,使得G可以复现训练数据分布,并且D判断的概率处处都等于 1 2 \frac {1}{2} 21,即使得D难以分辨数据是真实的还是G生成的。
当G和D都由多层感知机来定义时,我们就可以通过利用反向传播来进行训练。同时在训练和生成样本的过程中,相比于之前的相关算法,它不需要任何的马尔科夫链和近似的推理网络。
在 I n t r o d u c t i o n Introduction Introduction和 R e l a t e d w o r k Related work Relatedwork作者介绍了和本文内容相关的一些知识,包括之前广泛使用的其他的相关的算法,具体可见论文相应部分。
对抗网络
下面我们根据对抗网络的思想,从数学公式的推导上对其做一个理性的认识,来逐步的推出文中的这个公式 min G max D V ( G , D ) = E x ∼ p d a t a ( x ) l o g D ( x i ) + E x ∼ p z ( z ) l o g ( 1 − D ( G ( z i ) ) ) \min \limits_{G} \max \limits _{D} V(G,D)=E_{x \sim p_{data}(x) } logD(x_{i})+E_{x \sim p_{z}(z)}log(1-D(G(z_{i}))) GminDmaxV(G,D)=Ex∼pdata(x)logD(xi)+Ex∼pz(z)log(1−D(G(zi)))
假设用 x i x_{i} xi来表示真实的数据样本, z i z_{i} zi表示噪声数据,其中 i = 1 , 2 , … , m i=1,2,…,m i=1,2,…,m, p x ( x ) p_{x}(x) px(x)表示真实数据分布的概率密度, p z ( z ) p_{z}(z) pz(z)表示噪声数据分布的概率密度, G ( z i ) G(z_{i}) G(zi)表示噪声通过生成器生成的数据,它和真实数据 x x x形成了一种所谓的对抗关系。 x i ⇌ G ( z i ) x_{i}\rightleftharpoons G(z_{i}) xi⇌G(zi)
D ( x ) D(x) D(x)表示判别器认为 x x x为真假的概率,当判别器认为样本越真时,它的值就越接近于1,具体来说:
- D ( x ) = 1 D(x)=1 D(x)=1:当判别器认为输入的样本是来自真实的数据分布
- D ( x ) = 0 D(x)=0 D(x)=0:当判别器认为输入的样本是通过生成器产生的
对于生成器来说,它希望生成的样本让判别器认为是真实的,公式化就是最大化 D ( z i ) D(z_{i}) D(zi),即 max D ( D ( G ( z i ) ) ) \max \limits_{D} (D(G(z_{i}))) Dmax(D(G(zi)));而对于判别器来说,它希望的是尽可能分辨出由生成器产生的样本,同时不分错真实的样本,即 max D ( D ( x i ) ) \max \limits_{D} (D(x_{i})) Dmax(D(xi))和 min D ( D ( G ( z i ) ) ) \min \limits_{D} (D(G(z_{i}))) Dmin(D(G(zi)))。
其中 max D ( D ( G ( z i ) ) ) \max \limits_{D} (D(G(z_{i}))) Dmax(D(G(zi)))和 min D ( D ( G ( z i ) ) ) \min \limits_{D} (D(G(z_{i}))) Dmin(D(G(zi)))表示的就是生成器和判别器的对抗过程。为了后面公式的整合和推导,我们将 max D ( D ( G ( z i ) ) ) \max \limits_{D} (D(G(z_{i}))) Dmax(D(G(zi)))和 min D ( D ( G ( z i ) ) ) \min \limits_{D} (D(G(z_{i}))) Dmin(D(G(zi)))做一下等价的变换,将其转换成如下的形式:
- G : G: G: min D l o g ( 1 − D ( G ( z i ) ) ) \min \limits_{D}log(1-D(G(z_{i}))) Dminlog(1−D(G(zi)))
- D : D: D: max D l o g D ( x i ) \max \limits_{D} logD(x_{i}) DmaxlogD(xi)、 max D l o g ( 1 − D ( G ( z i ) ) ) \max \limits_{D} log(1-D(G(z_{i}))) Dmaxlog(1−D(G(zi)))
其中使用 l o g ( 1 − D ( G ( z i ) ) ) log(1-D(G(z_{i}))) log(1−D(G(zi)))代替 D ( G ( z i ) ) D(G(z_{i})) D(G(zi))是为了保证 G G G在学习的初期就有很大的梯度;而添加 l o g log log是为了方便后面的求导过程。
接着我们将关于 D D D、 G G G的关系是合并得到: min G max D l o g D ( x i ) + l o g ( 1 − D ( G ( z i ) ) ) \min \limits_{G} \max \limits _{D} logD(x_{i})+log(1-D(G(z_{i}))) GminDmaxlogD(xi)+log(1−D(G(zi)))
在学习的过程中作者使用了小批次的随机梯度下降法,故定义 m m m为 m i n i − b a t c h mini-batch mini−batch的大小,下面我们将 m i n i − b a t c h mini-batch mini−batch中的所有数据相加再求平均,得到 min G max D 1 m ∑ i = 1 m l o g D ( x i ) + l o g ( 1 − D ( G ( z i ) ) ) \min \limits_{G} \max \limits _{D} \frac {1}{m} \sum_{i=1}^m logD(x_{i})+log(1-D(G(z_{i}))) GminDmaxm1i=1∑mlogD(xi)+log(1−D(G(zi)))
这样就求得了一个 m i n i − b a t c h mini-batch mini−batch的期望,也就得到了原文中的 V ( G , D ) V(G,D) V(G,D)的式子 min G max D V ( G , D ) = E x ∼ p d a t a ( x ) l o g D ( x i ) + E x ∼ p z ( z ) l o g ( 1 − D ( G ( z i ) ) ) \min \limits_{G} \max \limits _{D} V(G,D)=E_{x \sim p_{data}(x) } logD(x_{i})+E_{x \sim p_{z}(z)}log(1-D(G(z_{i}))) GminDmaxV(G,D)=Ex∼pdata(x)logD(xi)+Ex∼pz(z)log(1−D(G(zi)))
算法描述
下面是有关算法描述的伪代码

基本过程和上面分析公式推导的过程是一致的,其中需要注意几点:
- 这里作者使用的是小批次随机梯度下降法(Minibatch stochastic gradient descent)来训练
- 使用迭代的数值方法计算
- 作者强调了在学习的过程中,优化D的K个步骤和优化G的1个步骤交替进行,这样是保证G变化的足够慢,使得D保持在最佳值附近
- 使用梯度上升更新判别器,使用梯度下降更新产生器
- 在基于梯度的方法中,使用了动量法这个改进的方法
全局最优解的证明
对抗网络训练到收敛后,最优的判别器满足
D
G
∗
(
x
)
=
p
d
a
t
a
(
x
)
p
d
a
t
a
(
x
)
+
p
g
(
x
)
D^{*}_{G}(x) = \frac{p_{data}(x)}{p_{data} (x)+p_{g}(x)}
DG∗(x)=pdata(x)+pg(x)pdata(x)
即使得
p
g
=
p
d
a
t
a
p_{g}=p_{data}
pg=pdata
证明:对于任给的生成器G,判别器D训练的标准为最大化
V
(
G
,
D
)
V(G,D)
V(G,D),将
V
(
G
,
D
)
V(G,D)
V(G,D)转换为如下的形式:
V
(
G
,
D
)
=
∫
x
p
d
a
t
a
(
x
)
l
o
g
(
D
(
x
)
)
d
x
+
∫
z
l
o
g
(
1
−
D
(
G
(
z
)
)
)
d
z
=
∫
x
p
d
a
t
a
(
x
)
l
o
g
(
D
(
x
)
)
d
x
+
p
g
(
x
)
l
o
g
(
1
−
D
(
x
)
)
V(G,D)=\int _{x} p_{data}(x)log(D(x))dx+\int_{z}log(1-D(G(z)))dz=\int _{x} p_{data}(x)log(D(x))dx+ p_{g}(x)log(1-D(x))
V(G,D)=∫xpdata(x)log(D(x))dx+∫zlog(1−D(G(z)))dz=∫xpdata(x)log(D(x))dx+pg(x)log(1−D(x))
因为任意的
(
a
,
b
)
∈
R
2
(a,b)\in R^2
(a,b)∈R2且不包含
{
0
,
0
}
\{0,0\}
{0,0},
(
a
,
b
)
∈
{
0
,
1
}
(a,b)\in \{0,1\}
(a,b)∈{0,1},对于函数
y
−
>
a
l
o
g
(
y
)
+
b
l
o
g
(
1
−
y
)
y->alog(y)+blog(1-y)
y−>alog(y)+blog(1−y)在
a
a
+
b
\frac {a}{a+b}
a+ba处取得最大值,所以当
V
(
G
,
D
)
V(G,D)
V(G,D)取得最大值时,
p
d
a
t
a
=
p
g
p_{data}=p_{g}
pdata=pg。
如果将D的训练目标看做是条件概率 p ( Y = y ∣ x ) p(Y=y|x) p(Y=y∣x)的最大似然估计,当 y = 1 y=1 y=1时x来自 p d a t a p_{data} pdata,当 y = 0 y=0 y=0时x来自 p g p_{g} pg,则有如下的转换,更容易理解这个结果。
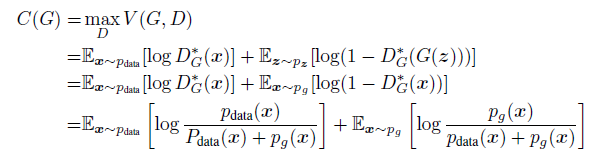
同时当 p d a t a = p g p_{data}=p_{g} pdata=pg时,C(G)取得最小值 − l o g 4 -log4 −log4。
算法收敛性的证明
当生成器G给定时,如果判别器D有足够的能力,则它能达到最优的效果,并且通过更新 p g p_{g} pg来提高以下这个判别标准 E x ∼ p d a t a [ l o g D G ∗ ( x ) ] + E x ∼ p g [ l o g ( 1 − D G ∗ ( x ) ) ] E_{x \sim p_{data}} [logD^{*}_{G}(x)]+E_{x \sim p_{g}}[log(1-D^{*}_{G}(x))] Ex∼pdata[logDG∗(x)]+Ex∼pg[log(1−DG∗(x))]使得 p g p_{g} pg收敛于 p d a t a p_{data} pdata。
证明:将 V ( G , D ) V(G,D) V(G,D)记为 V ( G , D ) = U ( p g , D ) V(G,D)=U(p_{g},D) V(G,D)=U(pg,D),把它看做是关于 p g p_{g} pg的函数,也是关于 p g p_{g} pg的凸函数,则该凸函数上确界的一次单数包括到达最大值处的该函数的导数。换言之,如果 f ( x ) = s u p α ∈ A f α ( x ) f(x)=sup_{\alpha \in A}f_{\alpha}(x) f(x)=supα∈Afα(x)且对每一个 α \alpha α, f α ( x ) f_{\alpha}(x) fα(x)是关于x的凸函数,那么如果 β = a r g s u p α ∈ A f α ( x ) \beta=argsup_{\alpha \in A}f_{\alpha}(x) β=argsupα∈Afα(x),则 ∂ f β ( x ) = ∂ f \partial{f_{\beta}(x)}=\partial{f} ∂fβ(x)=∂f。这等价于给定对应的G和最优的D,计算 p g p_{g} pg的梯度更新,如前面所证, s u p D U ( p g , D ) sup_{D}U(p_{g},D) supDU(pg,D)是关于 p g p_{g} pg的凸函数且有唯一的全局最优解,所以当 p g p_{g} pg的更新足够小时, p g p_{g} pg收敛于 p d a t a p_{data} pdata。
实验
作者在包括MNIST、TFD和CIFAR-10的数据集上来训练对抗网络。生成器网络使用的激活函数包括修正线性激活(ReLU)和sigmoid 激活,而判别器网络使用maxout激活。Dropout被用于训练判别器网络。
通过对G生成的样本应用高斯Parzen窗口并计算此分布下的对数似然,来估计测试集数据的概率。高斯的 σ \sigma σ参数通过对验证集的交叉验证获得,结果如下所示

该方法估计似然的方差较大且在高维空间中表现不好,但据我们所知却是目前最有效的办法。

用在图像问题中,我们也可以看出生成的图像很接近于真实图像。
算法的优缺点
缺点:
- p d a t a ( x ) p_{data}(x) pdata(x)只能隐式的表示
- 训练过程中D和G必须很好的同步
优点:
- 不需要马尔科夫链
- 仅使用后向传播来获得梯度
- 学习过程无需推理
- 模型可以融入多种函数
- 生成器只使用从判别器传来的梯度更新G
- 对于分布的表示很尖锐,即使是某些退化的分布
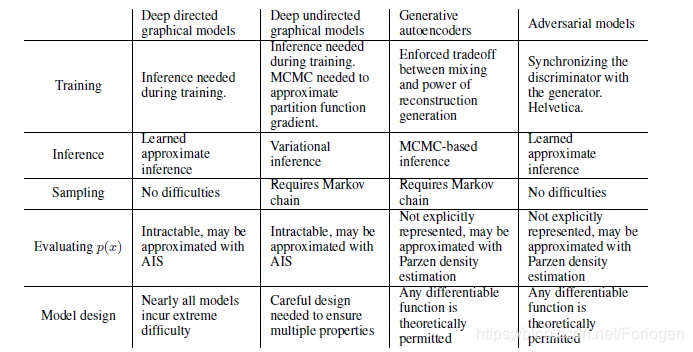
具体的和深度定向图模型、深度无定向图模型、生成自动编码器、对抗模型四种模型的对比如下
总结
最后作者给出了未来可以继续进行的工作的某些方向:
- 条件生成模型p(x∣c)可以通过将c作为G和D的输入来获得
- 给定x,可以通过训练一个辅助网络来学习近似推理以预测z。这和wake-sleep算法训练出的推理网络类似,但是它具有一个优势,就是在生成器网络训练完成后,这个推理网络可以针对固定的生成器网络进行训练
- 能够用来近似模拟所有的条件概率p(xS∣xS̸),其中S是通过训练共享参数的条件模型簇的关于x索引的一个子集。本质上,可以使用生成对抗网络来随机拓展确定的MP-DBM
- .半监督学习:当标签数据有限时,判别网络或推理网络的特征会提高分类器效果
- 效率改善:为协调G和D设计更好的方法或训练期间确定更好的分布来采样z,能够极大的加速训练。
通过阅读后面相关GAN改进的论文我们可以发现,它们很多的工作正是以上面提到的相关思路在做改进。
参考
论文地址: https://arxiv.org/abs/1406.2661
论文源代码: http://www.github.com/goodfeli/adversarial
个人总结:Generative Adversarial Nets GAN原始公式的得来与推导
Generative Adversarial Nets(译)
Generative Adversarial Nets[Vanilla]
GAN(Generative Adversarial Nets)的发展
Generative Adversarial Nets论文笔记+代码解析







 本文深入探讨了生成对抗网络(GAN)的基础理论,详细解释了GAN的工作原理及其数学公式推导过程。文章涵盖了GAN的基本概念、训练算法及其实验结果,同时讨论了GAN的优势与局限性。
本文深入探讨了生成对抗网络(GAN)的基础理论,详细解释了GAN的工作原理及其数学公式推导过程。文章涵盖了GAN的基本概念、训练算法及其实验结果,同时讨论了GAN的优势与局限性。
















 4655
4655

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








