林轩田机器学习技法第三讲-Kernel Support Vector Machine

上一讲讲到通过Dual Support Vector Machine我们最后的表达式看起来只与N有关，而和新转换域的维度d无关，但其实它隐藏在了Q的计算之中。这一讲来看一下，能否通过其他的方法来解决这个问题

首先回顾一下上一讲得到的表达式如下，通过二次规划的方法求解，得到α、w、b，从而最后等到我们的假设h，具体的求解过程可见上一讲。

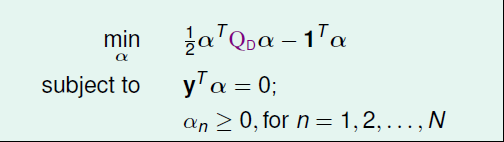
但是有一个问题就是在计算qn,m时涉及到ZnTZm（z是x经过特征转换而来的）的计算，如果从x空间来看的话， 分为两个步骤：1. 进行特征转换Φ1(xn)和Φ1(xm)；2. 计算Φ1(xn)和Φ1(xm)的内积。这种先转换再计算内积的方式，必然会引入参数d。当d很大的时候，计算量将会特别的大。我们希望通过一种方法来降低这个计算的复杂度，下面来看一下

比如在二次多项式转换后再做内积结果如下所示，为了方便后面的计算，我们将X0=1加入

假设我们有 x 和 x ’ 两个点，经过线性转换计算Φ1(x)TΦ2(x’)，将数据带入后通过合并相同的项，最后转换成关于xTx’的内积的形式

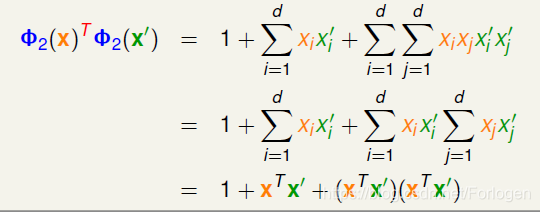
这时计算的复杂度由O(d^2)变成了O(d)，只与原始的X的空间维度d有关，这就解决了之前的问题

所以如果把特征转换和z空间计算内积这两个步骤合并起来，有可能会降低复杂度，简化计算。在二阶多项式会提高运算速度如果在更高阶的多项式中会怎么样呢？需要后面继续证明。

这里我们把合并特征转换和计算内积这两个步骤的操作叫做核函数(Kernel Function)，用大写字母K表示。例如刚刚讲的二阶多项式例子，它的kernel function为如下Φ2所示：

那么它是如何应用到SVM的呢？下面我们分别从其中的一些步骤中看一下，如何应用。比如在计算qn,m是涉及到Zn和Zm的内积，利用核函数后如下图红框所示的形式，通过计算等到qn,m，然后通过二次规划得到α；在计算b时如下绿框图所示，经过W的代换后引入核函数，同样可以将其变成与Z域无关的形式。在得到了α、W、b之后代入到gsvm(x)的表达式中，就得到了要求的g如下蓝框所示的形式

这样通过引入核函数，dual SVM中所需要求解的参数都得到了，而且整个计算过程中都没有在z空间作内积，即与z无关。把这个过程称为kernel trick，即把特征转换和计算内积两个步骤结合起来，用kernel function来避免计算过程中受的影响，从而提高运算速度

总结一下Kernel Hard-Margin SVM的整体的计算步骤如下，它只依赖于分类面上的支持向量，不受转换域维度d的影响，从而大大的提高了计算的效率

对应的每个步骤的时间复杂度如下所示

上面通过二次多项式推导出一个核函数KΦ2如下图所示，同样我们可以通过相关系数的放缩构成完全平方公式等得到不同的核函数

相同形式不同系数的核函数，会有不同的内积，反映到SVM中就会得到不同的距离，从而有不同的Margin，这样同样的数据得到的分类边界就会有区别。总结一下常用的K2(x,x’)形式的核函数如下所示

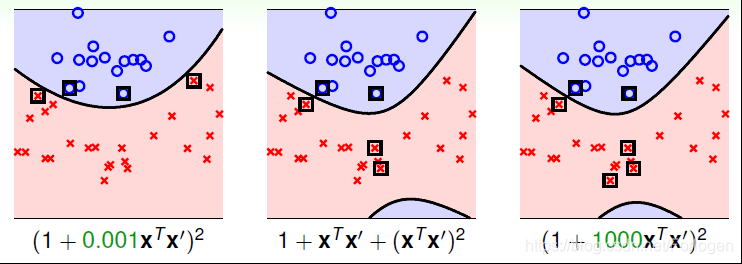
前面说到不同的转换，对应得到不同的距离，这是什么意思呢？如下所示，最初的一般的二次多项式的核反映到SVM的图像中，边界和支持向量如下中图所示；如果给γ取0.001时，对应的边界和支持向量如左图所示；如果γ取1000情况如右图所示。从中可以得出不同的系数对应了不同的边界和支持向量，效果直观上看好坏也有差距。所以选择合适的核函数和对应的系数，对于模型的效果影响很大

归纳一下，引入ζ和γ，对于Q次多项式一般的kernel形式可表示为：

使用高阶的多项式kernel有两个优点：
• 得到最大的margin，支持向量数量不会太多，分类面不会太复杂，减少复杂度，防止过拟合
• 计算过程避免了对d的依赖，减少了计算量

其中当Q=1时就是最简单的线性kernel，有时它就可以取得不错的效果。根据奥卡姆剃刀原则，如果可以用简单的kernel取得不错的效果，就不用使用更高阶的多项式kernel

前面讲到的特征转换是有限的，那么有没有可能转换到无限维的空间中，使用核函数的思想，来继续简化SVM的计算呢？很幸运，答案是可以的，下面我们就来看一下。例如，假设原始一维的空间中只有一个x，构造一个核函数为高斯函数，如下图蓝框所示。经过一系列的展开和合并，可以将K(x,x’)转换成Φ(x)Φ(x’)的形式，这其中Φ(x)形式如下绿框所示

这样得到的Φ(x)就可以是无限维的，将其称之为Gaussian Kernel。更一般的通过引入放缩因子γ，可以得到不同形式的高斯核

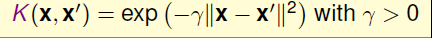
那么引入了高斯核函数，将有限维度的特征转换拓展到无限的特征转换中。有前面所学可知，由K(x,x’)，计算得到相关系数，进而得到gsvm。将k(xn,x)用高斯核函数代替，得到如下所示的形式，它由n个高斯函数线性组合而来，而且每一个高斯函数中心xn都是对应的支持向量，所以通常也将Gaussian Kernel称之为径向基函数(Radial Basis Function，RBF)

所以通过使用高斯核函数，我们就可以实现在无限维的空间中找到Large Margin

kernel SVM可以获得large margin 的边界，并且可以通过高阶的特征转换使Ein尽可能地小。Kernel的引入大大简化了dual SVM的计算量。而且Gaussian kernel能将特征转换扩展到无限维，并使用有限个支持数量的高斯函数构造出gsvm

同样的当γ取不同的值时，会有不同的高斯核函数，效果也会有不同，特别的当γ很大时，分类线会很复杂，模型就会发生过拟合。所以在使用高斯核函数时，γ的选择对于模型的效果至关重要

接下来我们来看一下不同的几种核函数的优缺点。首先是Linear Kernel，它是一种最基本的核，因为简单故计算量很小，通常使用现有的工具计算很快；而且解释性也很强。但是因为要求数据集是线性可分的，限制较强，当数据非线性可分时，效果就不太好了

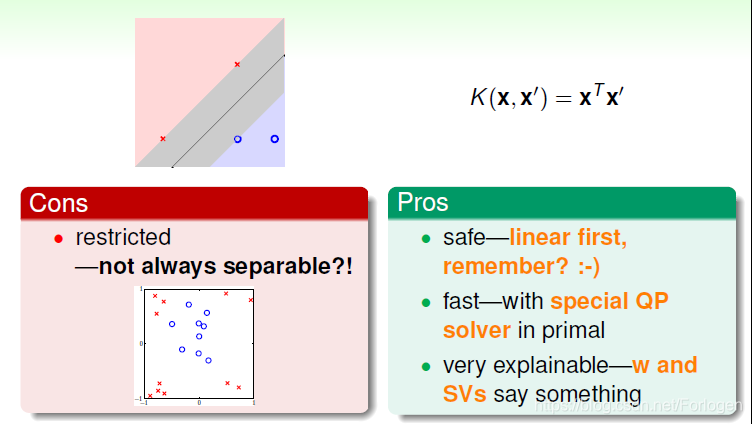
Polynomial Kernel的hyperplanes是由多项式曲线构成。它优点是阶数Q可以灵活设置，相比linear kernel限制更少，更贴近实际样本分布；但是当Q很大时，K的数值范围波动很大，而且参数个数较多，难以选择合适的值。所以如果低阶多项式核函数可以取得不错的效果，往往可以试一下使用Linear Kernel，可能会在不太损失模型的效果的基础上，减少计算量

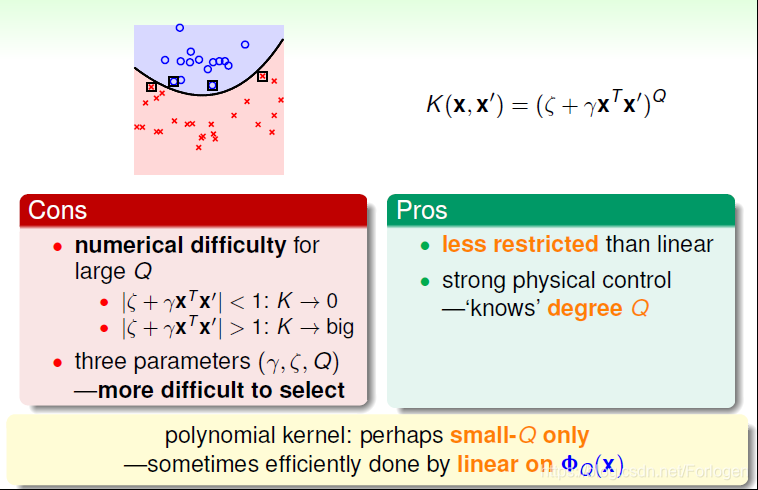
Gaussian Kernel的优点是边界更加复杂多样，能最准确地区分数据样本，数值计算K值波动较小，而且只有一个参数，容易选择；缺点是由于特征转换到无限维度中，w没有求解出来，计算速度要低于linear kernel，而且可能会发生过拟合

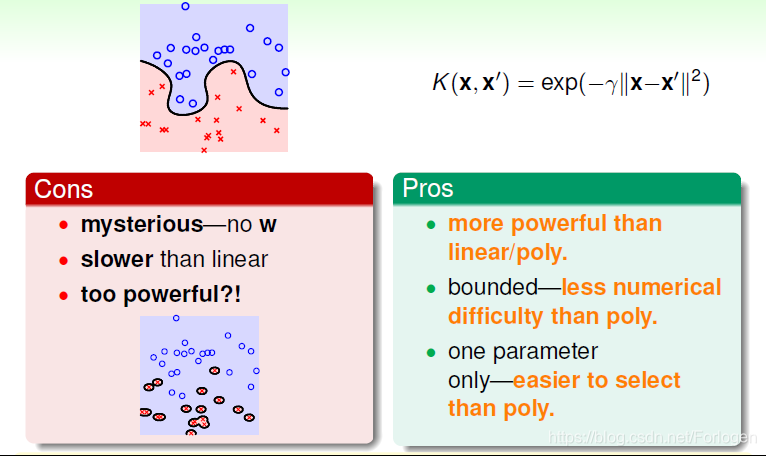
除了这三种之外，我们还可以使用其它形式的kernel。实际上kernel代表的是x和x’特征变换后的相似性。但是不能说任何计算相似性的函数都可以是kernel。有效的kernel还需满足几个条件：
• K是对称的
• K是半正定的
这两个条件不仅是必要条件，同时也是充分条件。所以，只要我们构造的K同时满足这两个条件，那它就是一个有效的kernel,这被称为Mercer 定理。

最后总结一下，这一将学习了多项式核和高斯核，并比较了讲到的几种核的优缺点。在实际的使用中，需要我们根据具体的情况，选择合适的核和对应的相关参数，来取得最好的效果