林轩田机器学习技法第二讲－Dual Support Vector Machine

上一讲学习了线性硬间隔支持向量机，如果数据集是线性可分的，在得到我们的目标表达式和它的限制条件后，可以使用二次规划的方法进行求解；如果是非线性可分的，通过线性转换到其他的域中，同样可以使用线性可分的方法来做。

这一讲学习Dual Support Vector Machine，即对偶支持向量机，希望找到一种其他的更好的方法进行求解。

在上一讲的Linear Hard-Margin SVM中，我们最后得到求解目标表达式和限制条件如左下图所示，通过和二次规划问题进行形式上的对照，可以借助有关的现有库输入对应参数进行求解，从而得到$g_{svm}(x)$。这里的$\varphi (x)$是指线性转换，针对域处理数据是非线性可分的问题

在线性可分数据集上，使用线性支持向量机得到最大间隔后，通过较小模型的dvc，降低了模型的复杂度；在处理非线性可分的问题时，通过线性转换将其变成线性可分的问题，是的模型变得简单易处理，得到更小的$E_{in}$

我们知道通过相关的证明可以知道$d_{vc}\le d+1$成立，那么在新的域中，模型如果越复杂，则对应的维度$d+1$就会越大，当大到无限大时，问题将难以求解。

所以我们的目标就是希望SVM的结果不依赖于域的维度大小$d$

在之前的线性支持向量机中我们有d+1个变量，N个限制条件，使用二次规划方法求解；将其转换成它的对偶问题后，我们的变量个数变成N，限制条件为N+1个，这样来看最后的求解就变成了不依赖于d的形式，那么前面那个问题就不做考虑了。那么它是如何转变的呢？

上一讲和之前都提到过在正则化中，我们最小化$E_{in}(w)$时引入了限制条件$w^{T}w\le C$，我们通过引入$\lambda$（拉格朗日因子）代替$C$可以转换成$E_{aug}(w)$的形式，这样限制条件就转到了表达式中

通过求解这个最小化问题，可以得到最后的最优解如下图所示。在正则化的问题中，$\lambda$是常数，容易求解，而在我们这一讲讨论的问题中，$\lambda$是未知的，因为限制条件有N个，那么它的个数也为N，在求解过程中同样需要对它求解

在引入拉格朗日因子$\lambda$后，求解的表达式就转换为了拉格朗日函数$L(b,w,\alpha )$的形式，如右下图所示（为了和其他的文献统一，使用$\alpha$代替$\lambda$），这样就是一个非条件问题

这样求解目标就是如下SVM的表达式，那么这样做是否正确呢？我们可以来想一下，在${\alpha }_n>0$的前提下，根据上面的限制条件可知，如果b和w不满条件，那么$1-y_n(w^T{z}_n+b)>0$，那么要得到最大值，${\alpha }_n$自然越大越好，大到$\infty$，无解；反之若$b和w$都满足条件，就有$1-y_n(w^T{z}_n+b)<0$，则$\alpha (1-y_n(w^T{z}_n+b))<0$，要得到最大值当且仅当$\alpha (1-y_n(w^T{z}_n+b))=0$成立，这时目标就变成了之前的求解目标了，表明这种方法是适用的。所以我们的目标表达式就是如上无条件的拉格朗日函数

经过证明知道得到的拉格朗日式子是正确的，则对于任意的固定的${\alpha }^{\prime }\ge 0$，下式都成立

因此对于固定的${\alpha }^{\prime }\ge 0$，可以转换成求它的最大化问题，同样成立

这种问题称之为拉格朗日对偶问题：即使表达式两边的max和min进行对调，求解问题仍然可行，将不等式的右边称为SVM问题的下界

那么现在的目标就是解这个下界

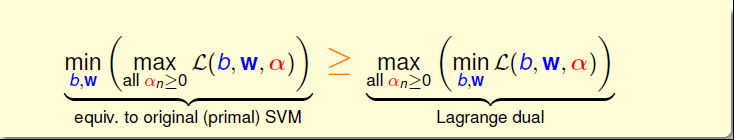
根据相关理论知道，这里的≥是一种弱对偶关系，在二次规划QP问题中，如果满足以下三个条件：
• 函数是凸的（convex primal）
• 函数有解（feasible primal）
• 条件是线性的（linear constraints）

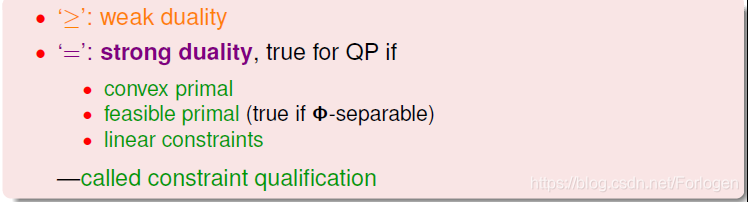
那么，上述不等式关系就变成强对偶关系，≥变成=，即一定存在满足条件的解$(b,w,\alpha )$，使等式左边和右边都成立，SVM的解就转化为右边的形式

因此将拉格朗日表达式带入后，求解表达式如下所示

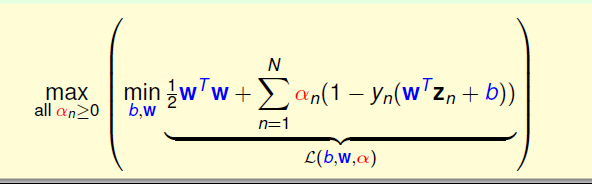
上式括号中的问题是一个无条件的问题，使用梯度下降法求解，对b求偏导令其为零，可得关于αn的等式，这是最优解必须满足的条件

将其回代就可以将b消掉，这时未知变量只有$w和\alpha$

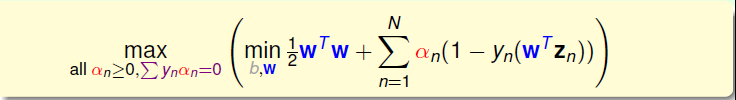
同理对$w$求偏导数为零的点，可得关于$w$的等式

同样将其回代到上式，经过化简，最终的表达式入式所示，它是只关于${\alpha }_n$的式子

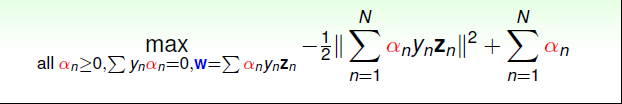
对应的KKT条件为，通过求解$\alpha$，就可以得到$w和b$，接下来的工作就是要求出$\alpha$

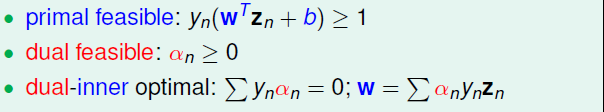
经过上面的转换，表达式为

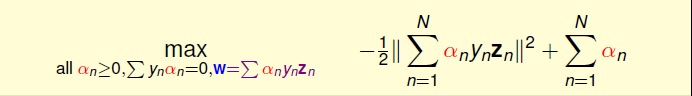
将其进行一些变换，变成更为熟悉求解的形式，这是未知变量还是N个，限制条件为N+1个

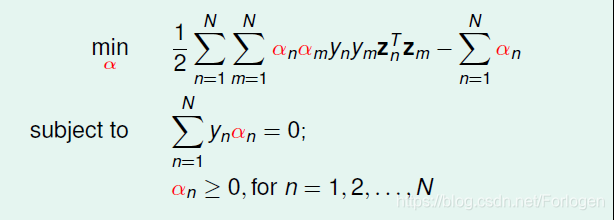
这个怎么求解呢？就要又用到二次规划了，将目标表达式和二次规划进行对照，找出对应的元素Q、p、A、c的值，使用现有的库即可求解

但是真的这么简单吗？仔细分析我们可以发现，$q_{n,m}$矩阵大部分值是非零的，当N很大的时候，计算QD的计算量将会很大，所以一般的方法不宜求解，需要使用专门针对SVM的二次规划求解的工具

假设经过相关工具的计算我们得到了α的结果，那如何返回来计算$w和b$呢？首先看一下之前的KKT条件，找到关于他们俩的式子。有关$w$的只有图中的一个等式，很容易求解；然后利用红框所圈的条件，任取一${\alpha }_n>0$ 的点，得到$1-y_n(w^T{z}_n+b)=0$，就可以求出$b=y_n-w^T{z}_n$。

这里满足$1-y_n(w^T{z}_n+b)=0$的点正好在分类的胖胖的线上，也就是说满足${\alpha }_n>0$的点一定在边界上，将其称为之前提过的支持向量(Support Vector)，反之说则不一定成立。所以之前也说过SVM只由支持向量决定，与其他的点无关。通过计算我们也可以确认这一点，当${\alpha }_n=0$时，无论$y_n、z_n$取什么值$W$都为零，所以计算$w和b$只需要属于支持向量的数据点

仔细回想一下W的计算式，好像和我们之前PLA的W求解的式子相似，$W_{svm}$由支持向量决定，$W_{PLA}$由分类错误的点决定，而且都是关于$y_n,z_n$的组合形式

本讲和上一讲介绍了两种形式的SVM，一种是Primal Hard-Margin SVM，另一种是Dual Hard_Margin SVM。Primal Hard-Margin SVM有d+1个参数，有N个限制条件。当d+1很大时，求解困难。而Dual Hard_Margin SVM有N个参数，有N+1个限制条件。当数据量N很大时，也同样会增大计算难度。两种形式都能得到w和b，求得fattest hyperplane。通常情况下，如果N不是很大，一般使用Dual SVM来解决问题

通过对偶形式的转换，最后的表达式只与N有关，但是其实并没有完全不依赖d，只是隐藏在了前面求$q_{n,m}$的过程中了

总结一下，这一将介绍了对偶支持向量机，通过引入拉格朗日因子，将表达式转换为非条件的只关于α的形式，结合KKT条件，使用专门为SVM设计的二次规划问题的求解工具即可求解，得到α、w、b