Stanford机器学习-推荐系统

这一讲来学习一下推介系统，这个东西在我们的日常生活中很常见也很重要，当你使用某些网站的时候，网站自动会为你推荐某些商品或是推荐某些视频作品，这些看起来总是和我们之前的购买历史或是浏览历史相似。那它背后是怎么运行的算法的原理是什么？这一讲来简单学习一下

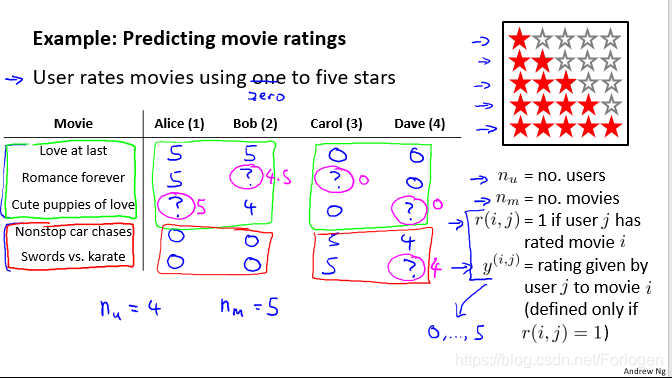
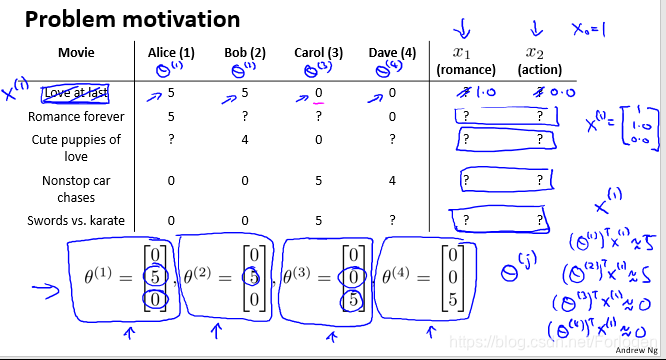
假设我们有如下的数据集，它包含五部电影，以及四位用户分别对它们的评价，评价从零星到五星，有的电影没有评价就用？标注。为了方便后面公式化的推导，规定了一些符号表示：
• nu ：代表用户的数量 代表用户的数量 代表用户的数量
• nm ：代表电影的数量 代表电影的数量 代表电影的数量
• r(i,j)：如果用户 如果用户i给电影 j评过分，则 r(i,j)=1
• y(i,j)：代表用户 i给电影j的评分，取值0-5
• mj：代表用户j评过分的电影总数

如何根据数据中已经给定的内容来到达推荐的目的呢？假设我们认为的为这个数据集规定了两个特征：x1代表电影的浪漫程度属性，x2代表电影的动作程度属性。这样我们给每个电影一个特征向量，例如x(1)=[0.9,0]，浪漫程度是0.9，动作程度是0：

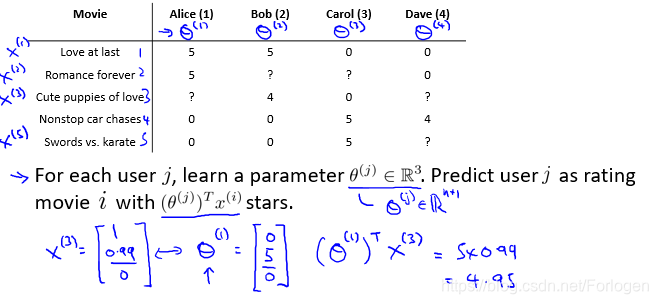
接着基于这些特征，为每一个用户构建一个线性回归模型，用向量θ表示，例如θ(1)是第一个用户的模型参数，于是有
• θ(j)： 用户 j 的参数向量
• x(i)：电影 i 的特征向量
• (θ(j) )^Tx(i):用户 j 对电影 i的预测评分为

针对用户 j，该线性回归模型的代价为预测误差平方和，加上一化项，则代价函数如下所示，这里加入了正则化项。

上面的代价函数针对于某一具体用户，为了学习所有的用户，我们将所有用户的代价函数求和

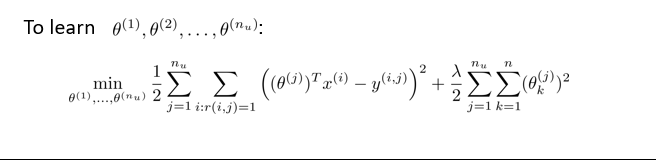
为了求解，我们可以使用梯度下降法

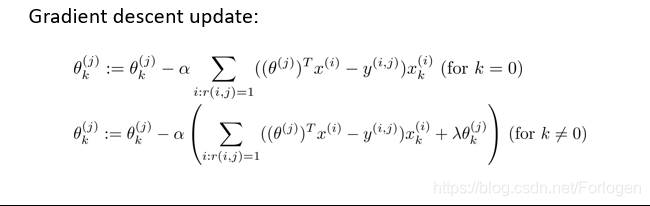
这样我们就可以根据每部电影的可用特征训练出每一个用户的参数，同理相反的，如果我们拥有了用户的参数，也可以学习到电影的特征

公式化的表示如下

但如果我们两者的数据都没有的话，方法就不可行了。这时就需要协同过滤算法（Collaborative filtering）出马了，它可以同时学习两者。我们的优化目标改为同时针对x和θ进行

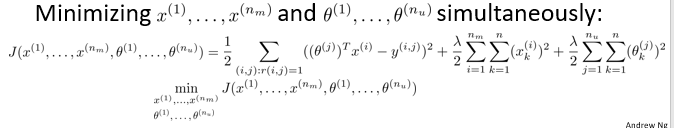
同样使用梯度下降法求解

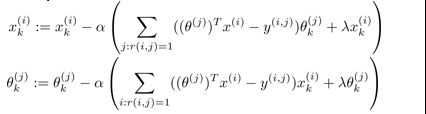
总结一下协同过滤算法的步骤如下：
1. 初始 x(1),x (2),…,x (nm)，θ(1),θ(2),…, θ(nu)为一些随机小值
2. 使用梯度下降算法最小化代价函数 使
3. 在训练完算法后，我们预测 (θ(j))^Tx(i)为用户 j 给电影 i 的评分
例如，如果一位用户正在观看电影 x(i)，我们可以寻找另一部电影 x(j) ，可以依据两部电影特征向量之间的距离 ||x(i)-x(j) || 的大小来推荐相关的电影，这就类似我们之前学习的K近邻算法了。

接下来介绍它的向量化的实现，以及说一下使用它你可以做的其他事情。例如：给出某件商品时，你能否找到和它相关的产品，或是根据用户的购买历史，为他推荐相关的产品。这里仍使用前面电影的例子来说明，将用户的评价用一个矩阵表示

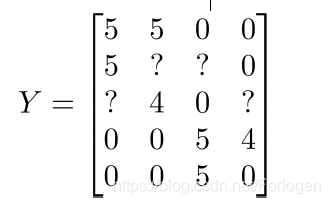
那么根据评分的计算公式，同样可以给出评分的矩阵

然后根据不同电影的特征向量之间的距离，寻找相关的影片

如果我们添加了一个新的用户Eve，而且他并没有为任何一部电影评分，那以什么为依据来为他推荐呢？

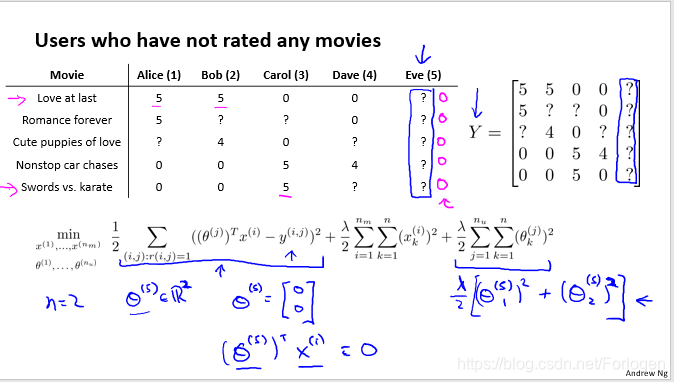
首先我们将Y矩阵进行均值归一化处理，将每一个用户对某一部电影的评分减去所有用户对该电影评分的平均值

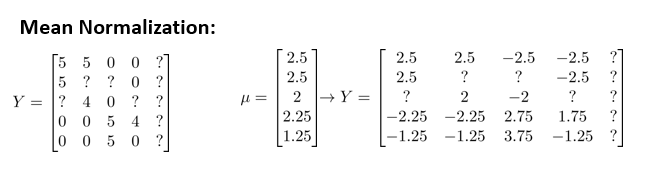
然后利用这个新的Y矩阵取训练算法，如果我们要用新训练出的算法来预测评分，则需要将平均值重新加回去，预测 (θ(j) )T(x (i))+μ i， 对于Eve，我们的新模型会认为她给每部电影 的评分都是该电影平均分