第三章 词法分析

Token和正则表达式

Token（词法单元）的内容：单词、单词类别(catalog)、内部码/内码(Inner_code)
一个单词中有多个不同的实例，才需要内部码来区分

单词的构造规则：

1. 通过正规文法（见第二章）
2. 正则表达式(Regular Expression)

正则表达式规则：

1. ε是最基本的正规表达式
2. 构造符号：
   | ：或
   • ：连接connect
   * ：闭包closure
   优先级：* >•> |
3. 正规表达式的特性：
   
4. 正则定义：给一些正规表达式命名，并在之后的正规表达式中像使用符号一样使用这些名字。

   一个正则定义是具有如下形式的定义序列：
   di → ri
   其中，每个di都是一个新符号，他们不在∑中，并且各不相同。而每个ri都是字母表∑∪{d1,d2,…, di-1}上的正规表达式。

5. 其他简化符号
   + ：一个或多个
   ? ：r?是r|ε的简写
   [a-z] ：代表从a开始到z的连续的字符组成的集合中的元素，即a|b|c|d|…|z

有穷自动机

状态转换图

• 状态state，用结点或圆圈表示。状态包括最终状态（又称接受状态，用双层圆圈表示）和开始状态（又称初始状态，该状态用一条没有出发结点的、标号为start的边指明）。在读入任何输入符号前，状态转换图永远处于开始状态。
• 边edge，从一个状态指向另一个状态。每条边的标号包含一个或多个符号。
  

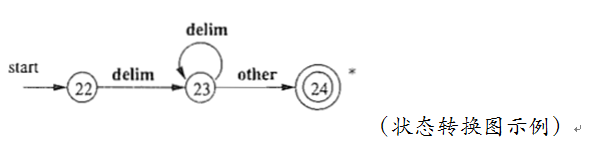
有穷自动机

有穷自动机（Finite automata，简称FA）是识别器，它们只能对每个可能的输入串简单地回答是或否。有穷自动机分为不确定的有穷自动机（NFA）和确定的有穷自动机（DFA）

FA的范式表达：
FA(S, s0, F, ∑, map/move)
S：有穷状态集合
s0：开始状态
F：终止状态的集合
∑：输入符号集合
Map：映射

DFA

确定的有穷自动机
对每个状态及自动机输入字母表中的每个符号，有且只有一条离开该状态、以该符号位标号的边（一对一）

NFA

不确定的有穷自动机
对其边上的标号没有任何的限制。一个符号标记离开同一状态的多条边，并且ε也可以作为标号（一对多）

转换

转换是一个重点，包括将正则表达式转换成NFA、把NFA转换成DFA、把DFA简化成DFA°

RE->NFA

从正则表达式到NFA的转换有两种算法，一种是较为简洁的分解法，但这种方法计算机没法使用。另一种就是在计算机中使用的Thumpson算法

分解法

1. 引入开始状态和结束状态。
2. 逐步分解
   
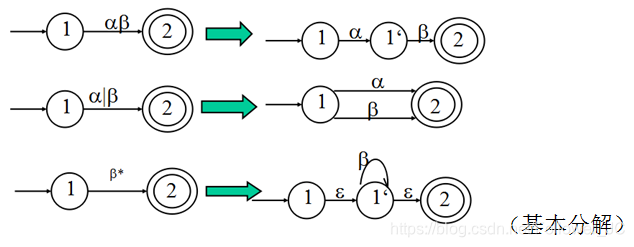
   实例：
   

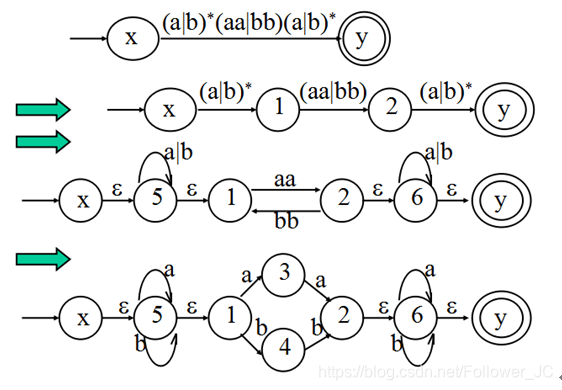
Thumpson算法

1. 把正则表达式的中缀形式转化成后缀形式。
2. 将后缀表达式从左向右依次做组合:
   
   

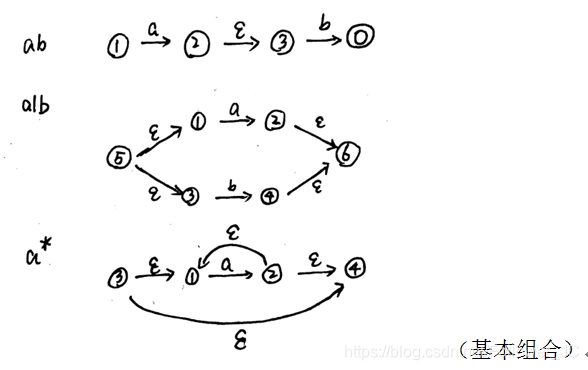
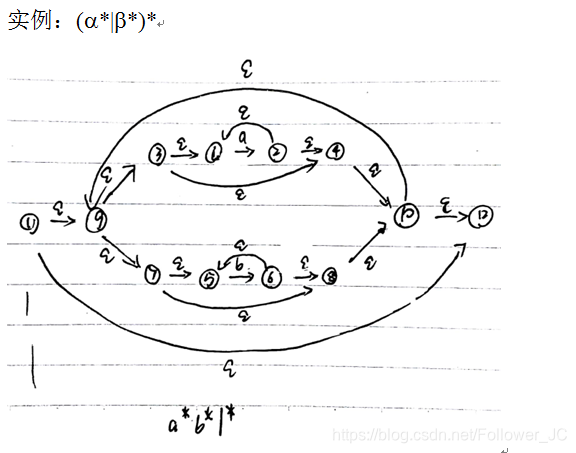
NFA->DFA

使用表格驱动：转换表
转化步骤：

1. 求出I0。I0=ε-closure({x})
2. 根据Ii求核(move操作)
3. 根据核求闭包，即为Ii+1
4. 重复2和3

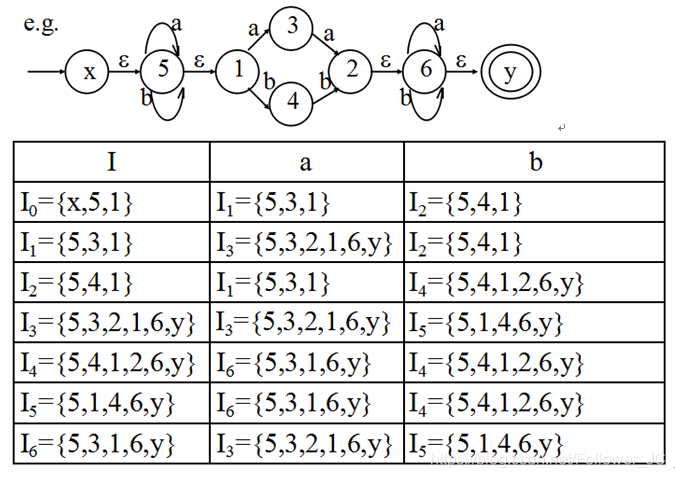
如何判断终止状态？
如果Ii∩F≠∅，那么Ii就是一个终止状态
在上面的例子中，终止状态包括：I3/I4/I5/I6

DFA->DFA°

DFA的优化就是使得DFA中的状态数最小化。
思想：自上而下分类。
首先理解一下状态等价的概念：

状态等价的概念：
当满足以下三个条件时，我们称两个状态是等价的：
① 两个状态发出的边数相同
② 每条边上所对应的标记也相同
③ 边的后续状态也是等价的。

强等价和弱等价：

• 强等价：后续状态相同
• 弱等价：后续状态属于同一个当前的叶子结点集合（当然随着后续叶子结点集合可能的分解，状态的等价性也会变化。见后文。）

优化步骤：

1. 首先把所有状态都当成一个等价类
2. 做低层分解，将状态分为终止状态和其他状态两个结点集合。
3. 对同一结点集合的每个状态做边转换。判断同一标记转化下的后续结点是否等价，由此做出分解。
4. 用一个结点替换掉一个等价结点集合里的所有结点

注：优化后的状态机中初始结点不能改变。