算法课的知识点（粗略）_全幺模矩阵-优快云博客

上了一学期算法课，感觉还是不怎么会，先记着，以后有机会，写在这里比较好找。还有就是希望以后能加入自己的思考（基本都是抄ppt），也许哪天心血来潮。写的也不全。🤭

基础知识

算法：一系列解决问题的清晰指令准确而完整的描述。

特征：可行性(若干有限时间结束的基本操作)，有穷性(有限次基本操作),确定性,有输入,有输出。

时间复杂度：针对指定基本运算(比较、加减乘除、内存交换)，算法执行运算的次数。

算法更关心随着n无限增长，T(n)的增长速度--渐进效率

渐进符号：用定义域为自然数集N的函数来定义算法的渐进运行时间

O记号(大写):渐进上界 Ω记号:渐进下界 o记号(小写):上界,没等于

ω记号:下界,没等于 Θ记号:满足Ω和O(大写)

仅保留多项式的最高阶项且去掉系数。

特性：传递性，自反性，对称性，转置对称性。

递归式算复杂度：迭代法、代入法、递归树方法、主方法。（还是手写快点，有点不知道怎么写）

分治

分治：递归地调用自身解决紧密相关的若干子问题

1. 分解原问题为若干互不相交的子问题

这些子问题是原问题规模较小的实例，与原问题属性相同

2.解决这些子问题，递归进行

如果子问题规模足够小则直接求解

3.合并这些子问题的解为原问题的解

递归的各子问题解决完后回到上一层进行合并

分治优化策略：用一部分子问题的解表达另一部分子问题减少计算子问题的个数

快速幂

int PowMod(int a, int b, int mod) {
    int ret = 1;   
    for(;b; b >>= 1, a = 1LL * a * a % mod)
        if(b & 1) ret = 1LL * ret * a % mod;
    return ret;
}

动态规划

动态规划：通过带备忘地组合子问题的解，求问题的一个最优解

动态：问题的解因时间或决策而变化规划：分解子问题,利用子问题之间关系求解

1、找出最优解的结构特征--最优子结构

问题的最优解是由哪些子问题的最优解以固定模式组成

这些子问题可能互有重叠

2、分析最优解与子问题最优解的关系--状态转移方程

分析得到计算公式，或者做表格来表示和计算

3、由子问题一步步算出更大问题的最优解

可以递归地自顶向下进行，也可以递推地自底向上

4、可利用推算过程还原最优解的具体方案

动态规划的两种等价实现方法，渐进复杂度通常一致

自底向上的递推:从小到大逐个解决子问题；
1. 优势:没有频繁的递归调用，常数更小
2. 劣势:思维量--需要预先确定好子问题规模大小，即求解的顺序
自顶向下的带备忘递归：对需要但尚未解决的子问题进行递归求解，否则直接返回备忘
1. 优势:1)思维量相对小，直接按状态转移方程实现，2)有的特殊情况下能跳过很多子问题
2. 劣势:递归开销，甚至面对有些过大的问题没有足够的递归栈

经典类型

有向无环图dp

特征：有向图，不存在环，转换为求其最长或者最短路径或路径计数。

状态转移方程：

int DPS(int i) {//例子：矩阵嵌套
    //dp,record初始化为-1
    int &ans = dp[i], &rcd = record[i];
    if(ans != -1) return ans;
    ans = 1;
    for(int j = 1; j <= n; j++)
        if(g[i][j] &&DPS(j) + 1 > ans){
            ans = DPS(j) + 1;
            rcd = j;
        }
    return ans;
}
//使用路径记录
void PrintBest(int best) {
    for(int i = best; i != -1; i = record[i])
        printf("%d ",i);
}

区间dp

int DPS(int l, int r) { // 例子：矩阵链乘法
    if(l == r - 1) return 0;    // 处理递归终点
    int &ans = dp[l][r];        // C++的引用，代码简洁些
    if(ans != -1) return ans;   // 备忘录已存在则返回结果，不重复计算
    ans = 0x3f3f3f3f;           // 初始化一个很大的数，便于更新求最小
    // 枚举“最后一次乘法发生的位置”，执行状态转移
    for(int i = l + 1; i < r; i ++) 
        ans = std::min(ans, DPS(l, i) + DPS(i, r) + a[l] * a[i] * a[r]);
    return ans;
}
void PrintAns(int i,int j) {
    if(i==j) {
        printf("A[%d]",i);
        return ;
    }
    //printf("(");
    PrintAns(i,record[i][j]);
    PrintAns(record[i][j] + 1, j);
    //printf(")");
}

背包dp

完全背包

for(int i = 1; i <= n;i ++){
    for(int j = 0;j <= b; j ++){
        dp[i][j] = dp[i - 1][j];
        if(j >= w[i])
            dp[i][j] = std::max(dp[i][j - w[i]] + v[i],dp[i -1][j]);
    }
}

滚动数组优化

for(int i = 1;i <= n; i++)
    for(int j = w[i]; j <= b; j ++)
        dp[j] = std::max(dp[j - w[i]] + v[i], dp[j]);

0-1背包

for(int i = 1; i <= n; i++)
    for(int j = b; j >= w[i]; j --)
        dp[j] = std::max(dp[j - w[i]] + v[i], dp[j]);

其他的

（有机会在补）

线性结构的dp

状态压缩dp

数位dp

树形dp

贪心

1. 找出可能的局部最优方案--贪心选择

每一步选择，都只剩下一个子问题(相对于动态规划有多个子问题)

2. 证明在贪心选择后，原问题仍能得到最优解

即贪心的选择是安全的

3. 满足最优子结构

子问题的最优解与上一步贪心选择能够组合得到原问题最优解

重在证明

反正法：作否定假设，则有更优解，进而推出矛盾
归纳法：证n = 1成立，假设n成立，推n + 1成立
交换论证：交换贪心方案的两个元素，答案不会变得更好或假设任意最优解，能通过等价交换得到贪心的方案

证伪：举反例

分数背包

区间类问题

经典问题

哈夫曼树

回溯

回溯法：解决搜索或优化问题，以合理顺序不重复不遗漏地枚举所有可能性。

上面这张图感觉看比较直观，好理解回溯，保存下来的。

搜索问题：寻找一个问题的某个可行方案，或者所有方案

优化问题：寻找一个问题的最优的方案

1. 分析问题地解空间

如生成排列是所有排列，生成子集是所有01串

2. 设计合理地枚举顺寻，形成搜索树

如排列树、子集树

3. 按搜索树顺序枚举，记录所需中间结果

n皇后

着色问题

回溯优化：求解组合优化问题

可行解：满足约束条件的解，例如01背包中不超过容量的若干物品

目标函数：关心的属性值，例如01背包中这些物品的价值

代价函数：当前子树最理想的可能性

界：已得到的最好的解

剪枝：在搜索树中，如果当前子树最理想的情况都比不上已得到的解，则该子树可以“剪掉”不再搜索，回溯父节点。

最大团问题

旅行商问题

等长的木棒

线性回归

一般形式

min或者max 目标函数

s.t. 约束目标

非负条件

自由变量

可行解：变量满足约束条件和非负条件的取值

可行域：全体可行解

最优解：目标函数最优的可行解

最优值：最优解的目标函数

标准型

目标函数：

约束条件(s.t.)：

特点：求最大、全部为不等式约束、全部非负约束

转换

目标函数统一，min变max，改为z` = -z,所有cj` = -cj
消除自由变量，变成全有非负约束的变量，自由变量xj替换成两数相减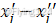,并约束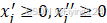
约束条件统一

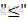
改变"=" ：替换为两个不等式，

改变 "≥": 两边乘-1

松弛型

约束条件引入s，变成 s为松弛变量，替换为加下去的x下标数

单纯形算法

（数学证明：交点即是最优点,寻找最优交点--通过Pivot）

基本变量：每个等式约束都有一个变量在等式左边(s)

非基本变量：等式右边及目标函数都有相同的变量集合(松弛型右边的x)

基本解：所有非基本变量设为0，计算得到基本变量后，所有变量的值

可行解：满足所有约束，包括非负约束

基本可行解：既是可行解又是基本解 (Pivot操作,非基本变量替换基本变量)

过程（不严谨）

找到第一个基本可行解（所有数非负，负的话要引入新变量x0，构造辅助线性规划问题）,再寻找基本变量对非基本变量约束最紧的（把不换的非基本变量和所有基本变量设为0，查看那个要换的非基本变量的值最小），不断寻找。

终止条件：目标函数的所有系数都不大于0，则目标函数达到最优；

目标函数某项系数为正，但约束条件该变量对应系数也为正，该变量的增加没有瓶颈，可以无限增长，此情况没有最优解

（潜在循环问题—Bland规则—选择替入替出变量时，满足条件前提下，选择下标最小的）

pivot操作代码

void Pivot(int l,int e){
    b[l] /= a[l][e];
    for(int j=0;j<n;++j){
        if(j != e) a[l][j] /= a[l][e];
    }
    a[l][e] = 1/a[l][e];

    for(int i=0;i<m;++i){
        if(i==l || a[i][e] > -eps && a[i][e]<eps) continue;
        b[i] -= a[i][e] * b[l];
        for(int j=0;j<n;++j){
            if(j!=e) a[i][j] -= a[i][e] * a[l][j];
        }
        a[i][e] = -a[i][e] * a[l][e];
    }
    z += c[e] * b[l];
    for(int j=0;j<n;++j){
        if(j!=e) c[j] -= c[e] * a[l][j];
    }
    c[e] *= -a[l][e];
}

double Solve(){
    while(true){
        int e=-1,l=-1;
        double maxc = eps;
        for(int j=0;j<n;++j){
            if(c[j]>maxc){
                maxc = c[j];
                e = j;
            }
        }
        if(e==-1) return z;
        double minba = inf;
        for(int i=0;i<m;++i){
            if(a[i][e] > eps && minba > b[i]/a[i][e]){
                minba = b[i]/a[i][e];
                l = i;
            }
        }
        if(l==-1) return inf;
        Pivot(l,e);
    }
}

还是要确定一下a，b，c对应输入的数据。

对偶型线性规划

求max变求min，约束条件变大于等于

性质：

设x是原始线性规划P的可行解，y是对偶线性规划D的可行解

则恒有：

因为

定理：如果x和y分别是原始线性规划P，对偶线性规划D的可行解，且cTx=bTy，则x和y分别是它们的最优解你

算法上：a（非基本变量的系数）转置，确定哪个是目标函数的c，哪个是约束条件的b

		对偶规划
		有最优解	有可行解且无界	无可行解
原始规划	有最优解	1	x	x
	有可行解且无界	x	x	2
	无可行解	x	2	3

整数线性规划

定义：

整数线性规划：再线性规划上要求变量是整数

纯整数线性规划(全整数线性规划)：要求所有变量是整数

混合整数线性规划：只要求部分变量是整数

0-1型整数线性规划：要求所有变量是1或0

全幺模矩阵：一个矩阵的任何子方阵的行列式等于+1，-1或0；二分图的无相关联矩阵是全幺模矩阵；如果一个0-1矩阵的每一行或每一列的1是连续的，那么可以判定为全幺模矩阵

如果一个线性规划的约束矩阵A是全幺模矩阵：则该线性规划一定有整数最优解

顺便吐槽一下这个编辑的，有点难用，写完才让我登录。。。。