FFT算法（附python代码）

原创已于 2024-12-07 10:29:43 修改 · 4.4k 阅读

60 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #机器学习 #人工智能 #嵌入式硬件

于 2024-12-02 17:34:36 首次发布

算法专栏收录该内容

2 篇文章

订阅专栏

快速傅里叶变换（FFT）简介

1. 什么是傅里叶变换（Fourier Transform）？

快速傅里叶变换（FFT）简介

FFT（Fast Fourier Transform，快速傅里叶变换）是计算离散傅里叶变换（DFT，Discrete Fourier Transform）的高效算法。它用于将时域信号转换为频域信号（即频谱），帮助分析信号的频率成分、幅值和相位。

1. 什么是傅里叶变换（Fourier Transform）？

傅里叶变换是一个数学工具，用于将时域信号（随时间变化的信号）分解为多个频率分量的组合。它的核心思想是：任何周期信号都可以表示为一系列正弦波和余弦波的叠加。

连续傅里叶变换公式

给定一个连续信号 x(t)x(t)，其傅里叶变换为：

2.离散傅里叶变换（DFT）

实际应用中，信号通常是离散的（数字化信号），傅里叶变换的离散形式称为离散傅里叶变换（DFT）。

DFT公式

对于一个长度为 NN 的离散信号 x[n]：

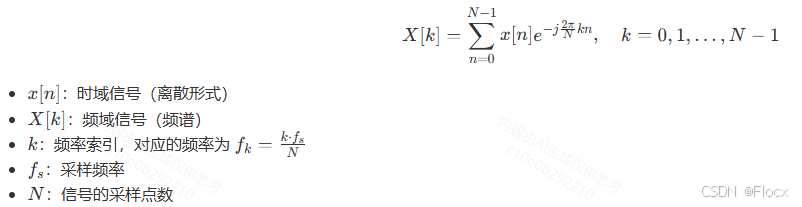
3.FFT的意义

FFT 是计算 DFT 的一种快速算法，时间复杂度从降低到。这种高效性使得傅里叶变换能被广泛应用于实时信号处理、图像处理等领域。

通过快速傅里叶变换（FFT），我们可以将时域信号转换到频域，从而更容易地识别信号中的频率成分。对于复杂的信号，时域分析往往难以揭示其频率特征，而频域分析方法（如滤波、频谱分析和数据压缩）能够更直观地展示信号的频率信息。

4.核心思想

FFT 通过分治法将大规模的 DFT 计算拆分成多个小规模的 DFT，从而减少重复计算。例如：

将一个 N 点的 DFT 分解成两个 N/2点的 DFT。
继续将每个子问题再拆分，直到无法再分解。

5. FFT的计算结果

FFT 的输出是一个复数数组，每个值包含两个信息：

幅值：频率分量的强度。幅值=
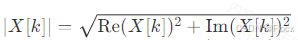
相位：频率分量的初始相位。相位=

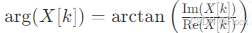
6. FFT的频率分布

输出数组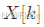包含正频率和负频率：
一般只需关注正频率部分。

频率与索引的关系

对应频率为：

时域和频域简介

1. 时域

时域分析是指直接在时间轴上观察和分析信号的方法。在时域中，信号被表示为时间的函数，即 x(t) 或 x[n]（对于离散信号）。

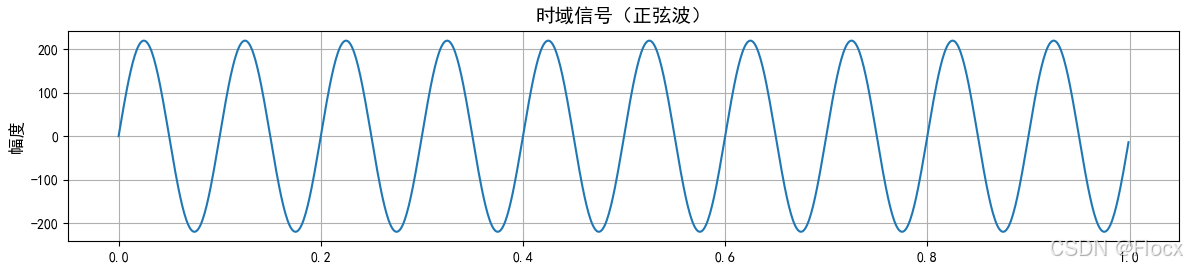
正弦信号可以用以下数学表达式表示：

其中：

A 是振幅，表示信号的最大值。
ω 是角频率（单位：弧度/秒），由 ω=2πfω=2πf 定义，其中 ff是频率。
θ是相位角，表示信号的初始偏移量。

正弦信号的性质

x(t) 是一个实数函数，因为在任何时间点 t，其值都是实数。
由于没有直接包含虚数部分，可以认为信号的“虚部”为 0。

1.1 时域信号的特点

直观性：时域信号直接反映了信号随时间的变化，容易理解和可视化。
瞬时值：可以直接观察到信号在任意时间点的瞬时值。
波形特征：可以观察到信号的波形特征，如周期性、脉冲、噪声等。

1.2 时域分析的应用

信号检测：检测信号中的特定事件或特征，如脉冲检测、故障检测等。
信号滤波：通过时域滤波器去除噪声或提取有用信号。
信号合成：通过时域操作合成复杂信号。

1.3 常用的时域分析工具

示波器：用于观察信号的波形和瞬时值。
卷积：用于信号的滤波和合成。
傅里叶变换：将时域信号转换到频域，以便进行频域分析。

2. 频域分析

频域分析是指通过傅里叶变换将信号从时域转换到频域，从而在频率轴上观察和分析信号的方法。在频域中，信号被表示为频率的函数，即 X(f)或X(ω)。

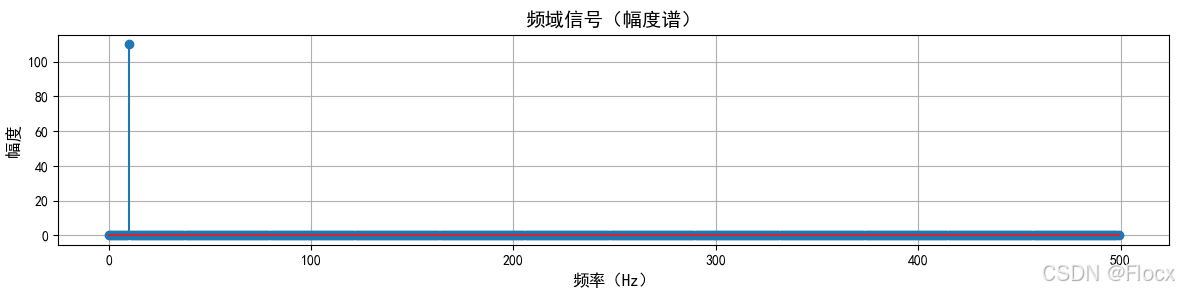
经过傅里叶变换，信号会被分解为不同频率的分量。变换结果通常表示为复数形式：

实部（Re）：与余弦分量相关，反映信号的振幅。
虚部（Im）：与正弦分量相关，决定信号的相位。

计算幅值和相位

傅里叶变换后的复数结果包含频率分量的幅值和相位信息：

幅值：表示信号在某频率下的强度，计算公式为：

相位：表示信号相对于参考信号的偏移，计算公式为：

atan2(Im,Re) 是一种扩展的反正切函数，可正确处理所有象限的相位角。

2.1 频域信号的特点

频率成分：频域信号直接反映了信号的频率成分，可以清楚地看到信号中包含的各个频率分量的幅度和相位。
频谱：频域信号的频谱可以显示信号的能量分布，有助于分析信号的频带宽度和带宽。
周期性：周期信号在频域中表现为离散的频率分量。

2.2 频域分析的应用

频谱分析：分析信号的频率成分，用于通信、音频处理等领域。
滤波设计：设计和实现频率选择性滤波器，如低通滤波器、高通滤波器、带通滤波器等。
调制与解调：在通信系统中，通过频域分析进行信号的调制和解调。

2.3 常用的频域分析工具

傅里叶变换：将时域信号转换为频域信号。
- 连续傅里叶变换：用于连续时间信号
- 离散傅里叶变换：用于离散时间信号
频谱分析仪：用于观察和分析信号的频谱。
拉普拉斯变换：用于连续时间信号的频域分析，特别适用于系统分析和控制理论。

3. 时域与频域的关系

时域和频域是信号的两种不同表示形式，它们之间通过傅里叶变换相互转换。傅里叶变换提供了将时域信号转换为频域信号的数学工具，而逆傅里叶变换则将频域信号转换回时域信号。

注意：在频域表示中，时域信号的幅值会表现为一半的衰减，这是由于傅里叶变换的性质和双边谱的定义所导致的。以下是具体原因

傅里叶变换将时域信号分解为不同频率的正弦分量。计算过程中，结果通常是一个双边谱，即包含正频率和负频率。
在双边谱中，每个频率的幅值会被均匀分配到正频率和负频率。

例如：

对于一个幅值为 A 的正弦信号，其频谱在正频率和负频率上分别有一半的幅值，即 A/2。
如果我们只取正频部分（单边谱），幅值会是时域信号的一半。

python生成时域和频域图

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
# MADE BY Flocx CXH
# 设置中文字体
rcParams['font.family'] = 'SimHei'  # 黑体（Windows常见）
rcParams['axes.unicode_minus'] = False  # 正常显示负号

# 参数设置
fs = 1000  # 采样频率（Hz）
t = np.arange(0, 1, 1/fs)  # 时间向量（从0到1秒，步长为采样间隔）
f = 10  # 正弦信号频率（Hz）
A = 220  # 正弦信号幅度

# 生成正弦信号
sine_wave = A * np.sin(2 * np.pi * f * t)

# 计算傅里叶变换
fft_values = np.fft.fft(sine_wave) / len(sine_wave)  # 归一化
fft_freqs = np.fft.fftfreq(len(fft_values), d=1/fs)

# 提取正频部分
positive_freqs = fft_freqs[:len(fft_freqs)//2]
positive_fft_values = np.abs(fft_values[:len(fft_values)//2])

# 绘制时域信号
plt.figure(figsize=(12, 6))

plt.subplot(2, 1, 1)
plt.plot(t, sine_wave)
plt.title("时域信号（正弦波）", fontsize=14)
plt.xlabel("时间（秒）", fontsize=12)
plt.ylabel("幅度", fontsize=12)
plt.grid()

# 绘制频域信号
plt.subplot(2, 1, 2)
plt.stem(positive_freqs, positive_fft_values)
plt.title("频域信号（幅度谱）", fontsize=14)
plt.xlabel("频率（Hz）", fontsize=12)
plt.ylabel("幅度", fontsize=12)
plt.grid()

# 显示图像
plt.tight_layout()
plt.show()