「图解大厂面试高频算法题」链表专题-环形链表(快慢指针)动图讲解

本文链接：https://blog.youkuaiyun.com/Flames_and_Lights/article/details/121881296

本文通过图解方式详细介绍了如何使用快慢指针解决链表中环形判断的问题，这是大厂面试中常见的算法题。快慢指针的思想是，一个指针每次前进一个节点，另一个指针每次前进两个节点，若存在环，两者最终会在环内相遇。此外，还提到了使用哈希表的解法，但空间复杂度较高。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

「图解大厂面试高频算法题」链表专题-环形链表(快慢指针)动图讲解

PS: 本文为「图解大厂面试高频算法题」专题，主旨是根据“二八法则”的原理，以付出20%的时间成本，获得80%的刷题的收益，让那些想进互联网大厂的人少走些弯路。

PS: 欢迎关注我获取更多大厂面试总结。

原题链接: https://leetcode-cn.com/problems/linked-list-cycle/

PS: 这道题虽然也是easy的，我最初开始做这道题的的时候，只能想到使用哈希表的方式。如果你在面试中指想到了用哈希表来解决，那面试官可能不是很满意噢。

题目介绍

给你一个链表的头节点 head ，判断链表中是否有环。
如果链表中存在环，则返回 true 。否则，返回 false 。

示例1

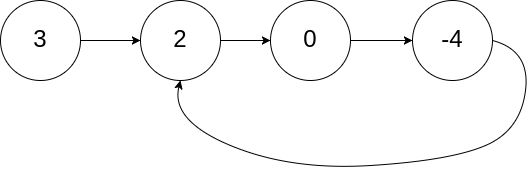
在这里插入图片描述

输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

题目解答

方法一：哈希表

思路和算法

最容易想到的方法是遍历所有节点，每次遍历到一个节点时，判断该节点此前是否被访问过，不过这个实现需要额外的存储空间，解法不是最优的，这个解法的难度确实是easy的。
以为这个方法的思路比较简单，我就不上图解了，直接上代码。

代码实现

public class Solution {
    public boolean hasCycle(ListNode head) {
        Set<ListNode> seen = new HashSet<ListNode>();
        while (head != null) {
            if (!seen.add(head)) {
                return true;
            }
            head = head.next;
        }
        return false;
    }
}

复杂度分析

时间复杂度：O(N)
空间复杂度：O(N)

方法二：快慢指针

思路和算法

快慢指针思想才是这道题目的终极答案。如果链表有环，慢指针slow每次迭代一个节点，fast指针每次迭代两个节点，在未来某一时刻，fast和slow指针必定相遇。想象一下在学校的运动会上的400赛跑比赛中，小蓝同学跑的比较慢，小红同学跑的比较快。无论小蓝同学和小红同学是否在同一起跑线，小红最终都会追上小蓝。

图解

黄色节点：slow和fast指针的起始位置。
红色节点：fast指针。
蓝色节点：slow指针。
紫色节点：相遇的位置。

在这里插入图片描述

代码实现

public class Solution {
    public boolean hasCycle(ListNode head) {
        ListNode fast = head;
        ListNode slow = head;
        while (fast != null && fast.next != null) {
            fast = fast.next.next;
            slow = slow.next;
            if (slow == fast) {
                return true;
            }
        }
        return false;
    }
}