洛谷 P2660 zzc 种田

最新推荐文章于 2024-11-27 11:54:35 发布

原创最新推荐文章于 2024-11-27 11:54:35 发布 · 608 阅读

0 ·

CC 4.0 BY-SA版权

贪心同时被 2 个专栏收录

37 篇文章

订阅专栏

数论

13 篇文章

订阅专栏

本文提供了一道编号为P2660的种田问题的详细解答，采用数论与贪心算法相结合的方法，通过最大化正方形面积与周长的比值来寻找最优解。代码实现清晰，适合对算法优化感兴趣的读者。

P2660 zzc 种田

题目链接-P2660 zzc 种田
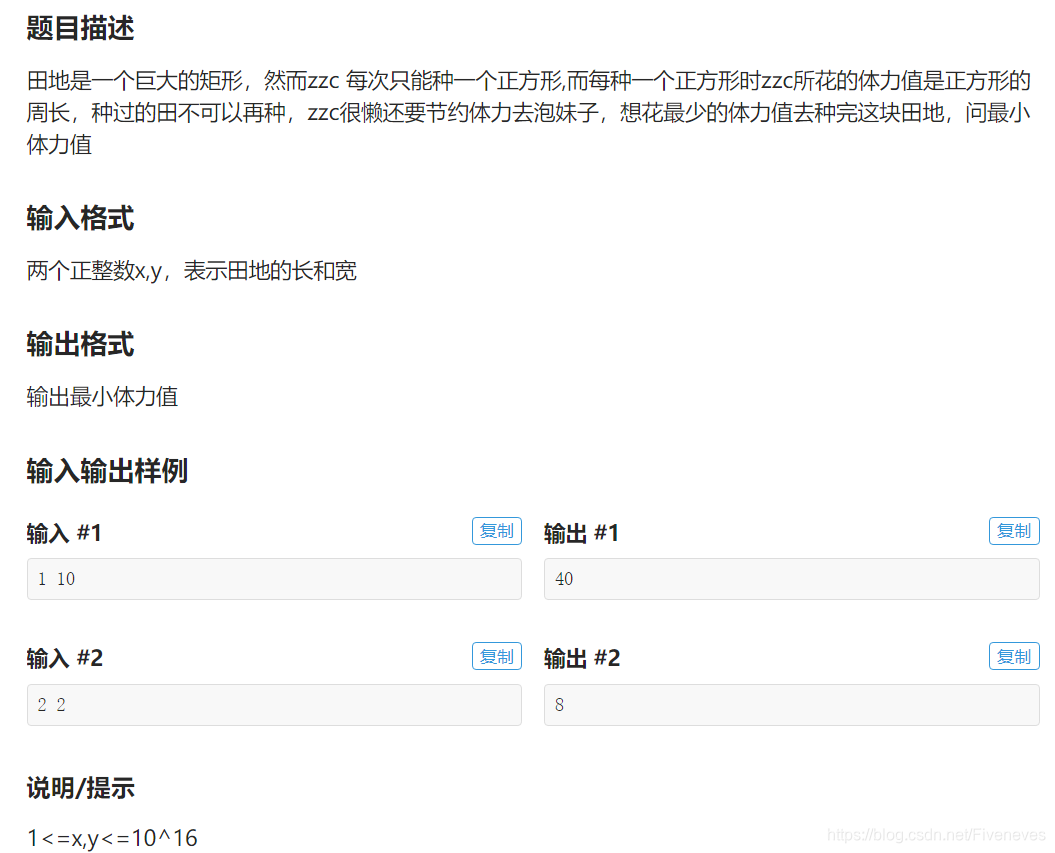
在这里插入图片描述
解题思路
数论+贪心

假设一个正方形边长为n，我们可以视正方形周长为代价，面积则为收益
因为总收益是一样的，所以我们找面积与周长比值最大的正方形即为最优解
因为k=n²/4n=n/4且每次都只能种一个正方形，所以每次都种最大的正方形即为正解
具体操作见代码
附上代码

#include<bits/stdc++.h>
#define int long long
#define lowbit(x) (x &(-x))
using namespace std;
const int INF=0x3f3f3f3f;
const int dir[4][2]={-1,0,1,0,0,-1,0,1};
const double PI=acos(-1.0);
const double eps=1e-10;
const int M=1e9+7;
const int N=1e5+5;
typedef long long ll;
typedef pair<int,int> PII;
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	
	int x,y,ans=0;
	cin>>x>>y;
	if(x>y) swap(x,y);
	while(x&&y){
		ans+=x*(y/x);
		y%=x;
		swap(x,y);
	}
	cout<<ans*4<<endl;
	return 0;
}